Работа № 4. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА РАСПРЕДЕЛЕНИЯ ВЕЩЕСТВА В ДВУХ НЕСМЕШИВАЮЩИХСЯ ЖИДКОСТЯХ

Целью работы является изучение коэффициента распределения ионов меди между водой и органической жидкостью при комнатной температуре.

При подготовке к работе следует ознакомиться со следующими разделами теоретического курса: правило фаз Гиббса, закон распределения, активности компонентов разбавленных, идеальных и реальных растворов.

Теоретические сведения

Рассмотрим систему из двух чистых жидкостей, нерастворимых друг в друге, при этом жидкости образуют два слоя. Если в такую систему добавить третье вещество, растворимое в обеих жидкостях (третий компонент), то после достижения равновесия этот третий компонент распределится между обоими слоями, образуя два раствора различной концентрации.

Согласно правилу фаз Гиббса число степеней свободы трехкомпонентной ( 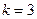) двухфазной ( 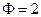) системы равно трем:

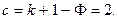(40)

Таким образом, из трех параметров, характеризующих равновесие системы (температура 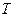и концентрации растворенного вещества в двух фазах 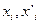), произвольно можно изменять лишь два. Третий параметр является функцией двух независимых переменных. При постоянной 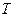концентрация растворенного вещества «i» в одной из фаз является функцией его концентрации в другой фазе, т.е. 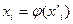. Другими словами, при равновесии двух фаз концентрации растворенного вещества «i» в них взаимно связаны. Эта связь выражается законом распределения вещества между двумя несмешивающимися жидкостями, согласно которому константа распределения, равная отношению активностей растворенного вещества в разновесных фазах является однозначной функцией температуры.

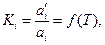(41)

Вывод уравнения (41) основан на условии равновесия системы: химические потенциалы растворенного вещества одинаковы в обеих фазах, т.е. .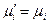

Используя известное соотношение

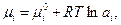(42)

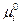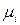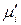в котором относится к стандартному состоянию, и приравнивая потенциалы и вещества «i», приходим к равенству:

.

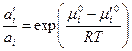(43)

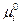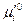Поскольку стандартные потенциалы компонента «i» в каждой из фаз и зависят лишь от температуры, отношение активностей компонента, называемое константой распределения, является также функцией только температуры и не зависит от состава растворов.

В реальных растворах активность компонента

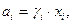(44)

поэтому вместо константы распределения удобнее использовать коэффициент распределения 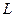, равный отношению концентраций растворенного вещества в равновесных фазах

.

(45)

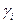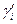Коэффициент распределения является функцией состава, поскольку коэффициенты активности и зависят от концентрации раствора.

В бесконечно разбавленных растворах коэффициент активности растворенного вещества постоянен, поэтому здесь не только константа, но и коэффициент распределения не зависят от состава равновесных фаз.

В бесконечно разбавленном растворе все величины, характеризующие состав, пропорциональны друг другу ( 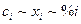). Поэтому здесь коэффициент распределения может быть выражен через отношение равновесных концентраций в любых единицах, например,

.

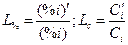(46)

Значения 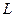при этом получаются различными, но во всех случаях они не зависят от состава.

Измерение коэффициента распределения позволяет определять активности растворенного вещества. Для этого бинарный раствор с известной зависимостью активности компонентов от состава приводят в контакт с несмешивающейся жидкостью, содержащей общий с первой фазой компонент, активность которого неизвестна. После установления равновесия измеряют концентраци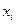и и 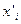растворенного вещества в каждой из фаз для растворов различного состава. Находят соответствующие значения отношений 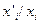и строят график зависимости этого отношения от концентрации третьего компонента в растворах с известными активностями. Экстраполируя полученную линию до нулевой концентрации ( 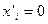), на оси ординат получают значение константы распределения для бесконечно-разбавленного раствора. Для таких растворов, как уже отмечалось, отношение концентраций растворенного вещества не зависит от состава растворов. Зная это отношение и величины активностей растворенного вещества в одном из растворителей, рассчитывают активности третьего компонента в другом растворителе при всех исследованных концентрациях.

Закон распределения имеет и другое важное практическое значение. Из предыдущих уравнений следует, что для понижения концентрации растворенного вещества в одной фазе при постоянных температуре и давлении необходимо понизить его концентрацию в другой. Последнее может быть достигнуто разбавлением одной из фаз. В частности, при производстве стали для очистки металла от вредных примесей (фосфора, серы и др.) либо увеличивают количество шлака, либо удаляют шлак, содержащий вредную примесь, и наводят новый. Так как при постоянной температуре константа распределения примеси остается величиной постоянной, то часть примеси переходит из металла в новый шлак и концентрация ее в металле уменьшается. Такое извлечение растворенного вещества из раствора называется экстракцией.

Очевидно, экстракция будет тем эффективнее, чем больше коэффициент распределения отличается от единицы. Коэффициент распределения можно менять, добавляя в растворы вещества, меняющие коэффициенты активности данного компонента «i». Так, введение вещества, имеющего большее сродство к данному компоненту, чем растворитель, снижает коэффициент активности этого компонента и, следовательно, изменяет величину коэффициента .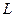

Порядок выполнения работы

Работа выполняется на виртуальной модели, которые часто применяются в случае, если изучение объекта экономически не обосновано, осложнено экспериментально или не безопасно. Виртуальная модель включает в себя смысловую модель, на основе которой разрабатывается математическая модель. По уравнениям мат. модели с помощью компьютера осуществляется графическое представление процесса.

Выполняемая виртуальная работа основана на реальном процессе выделения ионов меди из водного раствора при соприкосновении данного раствора с органической фазой представляющей собой раствор Д2ЭГФК ( Ди 2-этил-гексил фосфорная кислота) 30 мас.% в керосине. При протекании такого процесса основное количество Cu²⁺ переходит в органическую фазу, а концентрация Cu²⁺ в водном растворе существенно снижается.

Для выполнения работы следует подать в емкость 1 (Рис.8) по трубке 3 с помощью нажатия соответствующей кнопки-клапана необходимое кол-во водного раствора V_р (от 100 до 190 мл, синего цвета), добавить клапаном 4 жидкой органической фазы. После чего включить магнитную мешалку и перемешать растворы в течение 30 сек.

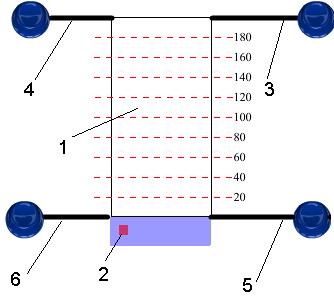
Рис. 8. Схема установки для разделения ионов меди между двумя несмешивающимися жидкостями: 1 – емкость для разделения (экстрактор), 2 – кнопка включения магнитной мешалки, трубки для подачи/слива: 3 – водного раствора содержащего ионы меди, 4 – органической фазы, 5 – на отбор проб для титрования, 6 – растворов в отстойник

Затем полученной эмульсии дают отстояться, и когда установятся два слоя, нижний (воду) в количестве 20 мл сливают нажатием на клапан трубки 5 в колбу для титрования 7 (Рис.9).

С помощью клапана 8 в бюретку 9 заливают титрующий раствор (водный раствор тиосульфата натрия) до выбранного уровня. К исследуемому раствору в колбе 7 добавляют 2 г KJ и 2 мл крахмала с помощью кнопки 10. При добавлении избытка KJ в исследуемый раствор вся медь содержащаяся в нем превращается в иодид и осаждается на дно сосуда.

2Cu 2+ +4I- = 2 CuI + I2

(47)

В ходе этой реакции происходит выделение молекулярного йода J₂ , который в присутствии крахмала придает раствору ярко синюю окраску.

Далее с помощью крана 11 начинают титрование, приливая титрующий раствор из бюретки в колбу 7. При этом осуществляется реакция:

I2 + 2 Na2S2O3 = 2 NaI + Na2S4O6.

(48)

Тиосульфат натрия взаимодействует с йодом, уменьшая его количество. В момент времени, когда весь молекулярный йод прореагирует по реакции (48), окраска раствора резко изменит свой цвет с синего на бесцветный. Как только раствор обесцветился титрование прекращают и фиксируют потраченное количество титрующего раствора V_т. Зная концентрацию тиосульфата натрия (Na₂S₂O₃) в титрующем растворе, равную 0,1 моль/л, рассчитывают по реакциям (1 и 2) концентрацию меди в исследуемом растворе С_р1. В соответствии с реакцией (47) 2 моля прореагировавших ионов меди приходится 1 моль выделившегося иода. И по реакции (48) для нейтрализации 1 моля иода необходимо 2 моля тиосульфата натрия.

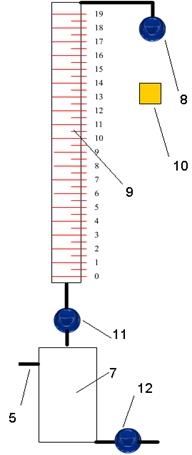
Рис. 9. Схема установки для титрования

7 – колба, 9 – бюретка, 10 – добавление KJ,

8,11, 12 – клапаны

То есть 1 моль прореагировавших Cu²⁺ приведет к затратам при титровании 1 моль Na₂S₂O₃:

.

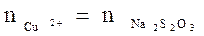(49)

Следовательно концентрацию С_р1 можно определить по формуле:

Ср1= 0,1*Vт/20.

(50)

При выполнении работы на экране в правом нижнем углу отображается начальная концентрация ионов меди в растворе подаваемом в экстрактор C₀ от 0,01 до 0,05 моль/л. До процесса экстракции водный раствор содержал количество меди равное 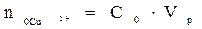. После того как произошло перераспределение, в растворе остались ионы меди в количестве 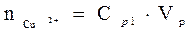. Следовательно в органическую фазу перешло количество меди равное 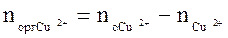. Зная перераспределившееся количество меди, определяют равновесную концентрацию меди в органической фазе С_р2.

В емкости, где происходит разделение, остался раствор в количестве достаточном для повторного осуществления операции титрования. Поэтому клапаном 12 сливают из колбы 7 раствор после титрования и проводят химический анализ повторно. Определение концентрации меди в исследуемом растворе осуществляют 3 раза. По результатам трех измерений определяют средние значения концентраций.

Используя уравнение (46) находят коэффициент распределения ионов меди между водой и органической фазой для одной равновесной концентрации ионов меди в воде. Изменяя соотношения объемов органической фазы и водной (водный раствор добавляется в количестве 190, 180, 170, 160, 150 мл; органический до метки в 200 мл), изменяют равновесную концентрацию ионов меди. Определяют зависимость коэффициента распределения L от концентрации. Результаты измерения и расчетов помещают в таблицу 5.

Таблица 5

Результаты работы

№ опыта	Количество раствора тиосульфата, V, мл	Концентрация, моль/л	Коэффициент распределения L
№ пробы	Vср, мл	С0	Ср1	Ср2

Вопросы для самоконтроля

1. Что называют константой распределения; от каких факторов зависит константа распределения?

2. Что называют коэффициентом распределения; в каком случае коэффициент распределения не зависит от состава раствора?

3. Чему равно число степеней свободы системы, состоящей из двух несмешивающихся индивидуальных жидкостей и распределенного между ними третьего вещества?

4. В каком случае по результатам опытов можно говорить о независимости коэффициента распределения от состава раствора?

5. В условиях задачи требуется очистить изоамиловый спирт от уксусной кислоты при помощи 1 литра воды. Коэффициент распределения равен 1. Как выгоднее ее использовать для этой цели: залить ли ее всю в делительную воронку сразу или отдельными порциями?

6. Изменится ли коэффициент распределения, если между двумя несмешивающимися фазами поместить третью фазу?

7. В чем состоит практическое значение определения коэффициента распределения вещества в двух несмешивающихся жидкостях?