Порядок расчета диска произвольного профиля

Вычерченный в масштабе диск последней ступени разбивается на 4 участка постоянной толщины, рис. VII.1. Размеры каждого участка определяются по эскизу. Вычисляются или задаются граничные условия (иначе говоря, известные или задаваемые произвольно радиальные и тангенциальные напряжения) на внутреннем и внешнем радиусах диска r₀ и r_a.

Граничные условия на внутреннем радиусе диска r₀ задаются по-разному для первого и второго расчетов.

Первый расчет. Для диска, насаженного на вал с натягом, истинное радиальное напряжение на внутреннем радиусе, создаваемое посадкой диска, составляет 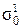= - (5 – 10) МПа. Тангенциальное напряжение 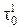принимается произвольно (например, 50 МПа). Для диска цельнокованого ротора со свободным отверстием в центре истинное радиальное напряжение на внутреннем радиусе 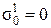, а тангенциальное 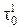принимается произвольно. Для диска сварного ротора без отверстия в центре радиальное и тангенциальное напряжения принимаются произвольно, причем .

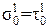Второй расчет. Для диска, насаженного на вал с натягом и диска цельнокованого ротора со свободным отверстием в центре, радиальное напряжение на внутреннем радиусе принимается 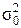= 0, а тангенциальное 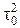- произвольным, не равным нулю (например, 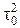=25 МПа). Для диска без отверстия принимаются новые произвольные значения 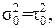не равные нулю (например, 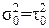= 25 МПа).

Граничное условие на внешнем радиусе диска r_a – это радиальное напряжение, создаваемое центробежной силой рабочих лопаток, МПа:

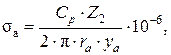
где С_р – центробежная сила одиночной лопатки, Н (определена в расчете лопатки, Приложение V); Z₂ – число рабочих лопаток; r_a = d_к/2 - внешний радиус диска (корневой радиус ступени), м; y_a = y₄ – толщина обода диска, м (рис. VII.1).