Изменение энтропии в химических реакциях

Перейдем от состояния вещества к процессам от абсолютных значений энтропий к их изменениям, обусловленным химическим взаимодействием. Зная значения стандартных энтропий можно рассчитать изменение энтропии при протекании химической реакции:

_∆rS⁰₂₉₈ = ΣviS⁰_298i (продуктов реакции) - ΣvjS⁰_298j(исходных веществ),

Так, для реакции v₁ А₁ + v₂ А₂ = v₃ А₃ + v₄ А_4;

_∆rS⁰₂₉₈ = [v₃S⁰_298(А3) + v₄ S⁰_298(А4) ] - [v₁S⁰_298(А1) + v₂S⁰_298(А2) ]

Например, для процесса протекающего при стандартных условиях

Н_2(г) + ½ О_2(г) = Н₂О_(ж); _∆rS⁰₂₉₈

_∆rS⁰₂₉₈ = S⁰₂₉₈ 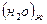- (S⁰_{298 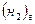+} ½ S⁰₂₉₈ 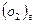) = 69,95 – 130,52 – ½ 205,04 = - 163,14 Дж/моль*К

Стандартная энтропия любого вещества является положительной величиной (S⁰₂₉₈ >0), изменения энтропии в процессах (_∆rS) могут быть положительными, отрицательными или равными нулю.

Температурная зависимость стандартной энтропии реакции.

Стандартная энтропия реакции при Т ≠ 298 К вычисляется с учетом теплоемкостей исходных веществ и продуктов реакции.

_∆rS⁰_(т) = _∆rS⁰₂₉₈ + 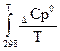dT (1.55)

Если считать, что теплоемкость не является функцией температуры _∆Ср_(Т) ≠ f(T), но после интегрирования получим:

_∆rS⁰_(т) = _∆rS⁰₂₉₈ + _∆Ср * ln 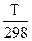(1.56)

При температурной зависимости теплоемкости, которая выражается степенным рядом:

_∆Ср⁰ = _∆а + _∆в * Т

формула (1.55) принимает вид:

_∆rS⁰_(т) = _∆rS⁰₂₉₈ + 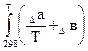dT = _∆rS⁰₂₉₈ + _∆а * ln 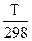+ _∆в (Т - 298) (1.57)

Изменение энергии Гиббса

Изменение энергии Гиббса - критерий направленности самопроизвольного процесса в закрытой системе. Реальные процессы происходят, как правило, в закрытых системах в изобарно-изотермических (р,Т = const) условиях, это наиболее типичный режим для самых различных процессов. Из уравнения (1.50) при р = const и Т = const находим

δА' ≤ - d (U + pv - TS) р,Т (1.58)

введем обозначение

δА' ≤ - d (Н - TS) (1.59)

G = H – TS (1.60)

Функция G является функцией состояния системы и называется энергией Гиббса или изобарно-изотермическим потенциалом. Энергия Гиббса при р,Т = const является экстенсивным свойством системы ее абсолютные значения не поддаются вычислению.

Для обратимого процесса

δА' = dА' max = - (dG) р,Т (1.61)

А' max = - (G₂ – G₁) = - (_ΔG) р,Т (1.62)

Отсюда для обратимого (квазистатического) процесса при рассматриваемых условиях максимальная (полезная) работа (А' max) приобретает свойства функции состояния и равна убыли энергии Гиббса.

Уравнение (1.60) можно переписать в виде Н = G + T * S, где энергия Гиббса характеризует ту часть полной энергии системы, которая может быть превращена в работу в изобарно-изотермический процесс. В этом состоит физический смысл величины G. Величина Т * S характеризует связанную энергию, т.е. ту часть полной энергии системы, которая рассматривается в окружающей среде в виде теплоты. Для установления критерия направленности самопроизвольного процесса в закрытой системе продифференцируем уравнение (1.60).

dG = dU + pdv + vdP – TdS – SdT (1.63)

Согласно выражению (1.52), ТdS ≥ dU + рdV

dU ≤ ТdS – рdV (1.64)

Подставим в уравнение (1.63) вместо dU большую либо равную ей величину ТdS – рdV получим следующие неравенство:

dG ≤ - S * dТ + Vdр (1.65)

Для изобарно-изотермического процесса (р,Т = const, dp = dT = 0) выражение (1.65) примет вид (dG)_р,Т ≤ 0, или для конечных изменений энергии Гиббса

(_ΔG)_р,Т ≤ 0 G → Gmin (1.66)

Следовательно, в закрытой системе знак изменения энергии Гиббса является критерием направленности самопроизвольного процесса при проведении его в изобарно-изотермических условиях:

1. если _ΔG = 0 (G → Gmin, энергия Гиббса достигла минимального значения), то система находится в состоянии термодинамического равновесия;

2. если _ΔG < 0 (G → Gmin, энергия Гиббса убывает), то процесс в данном направлении термодинамически возможен;

3. если _ΔG > 0, процесс в данном направлении термодинамически невозможен.

Применяя выражение (1.65) к обратимому равновесному процессу, получим

dG = – SdT + VdP (1.67)

из условия (1.67) вытекает

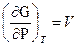(1.68)

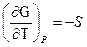(1.69)

Из соотношений (1.68) следует, что объем системы, служит мерой возрастания энергии Гиббса при увеличении давления при постоянной температуре, а энтропия – мерой убыли энергии Гиббса с возрастанием температуры при постоянном объеме. Такие функции состояния, частные производные которых по соответствующим отработанным параметрам состояния в явной форме выражают другие параметры, называются характеристическими. Подставляя (1.69) в (1.60), получим

G = H + T 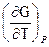, или для процесса (в том числе и для химической реакции) изменение энергии Гиббса при переходе системы из состояния 1 в состояние 2

_∆rG⁰_(т) = _∆rН⁰_(т) + Т 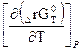, (1.70)

Где 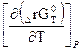= – _∆rS⁰_(т)

Выражение (1.70) называется уравнением Гиббса-Гельмгольца, оно связывает изменение энергии Гиббса химической реакции с ее тепловым эффектом и температурой. Иначе его можно записать в виде

_∆rG⁰_т = _∆rН⁰_т - Т_∆rS⁰_т (1.71)

Анализ уравнения (1.71) показывает, что знак и величина _∆rG⁰_т зависят от двух факторов: энтальпийного - _∆rН⁰_т и энтропийного Т_∆rS⁰_т . Соотношение этих факторов определяет термодинамическую возможность самопроизвольного протекания реакции в закрытой системе при р,Т = const.

С одной стороны, в ходе химической реакции система стремиться перейти к минимальному уровню энтальпии, выделив часть ее в форме теплоты (_∆rН⁰_т < 0), с другой стороны, система стремиться занять наиболее вероятное состояние, характеризующееся максимумом беспорядка, т.е. максимумом энтропии (_∆rS⁰_т > 0).

Если процесс протекает так, что _∆rН⁰_т = 0, то рост энтропии становится единственной движущей силой. И, наоборот, при условии _∆rS⁰_т = 0, движущей силой процесса является убыль энтропии.

Компенсация энтропийного и энтальпийного факторов соответствует установлению равновесия в системе.

_∆rН⁰_т = Т _∆rS⁰_т (1.72)

Изменение энергии Гиббса химической реакции при стандартных термодинамических условиях (р = 101,3 кПа, Т = 298 К) можно вычислить по уравнению _∆rG⁰₂₉₈ = _∆rН⁰₂₉₈ - _∆rS⁰₂₉₈ * 298;

Возможен и другой путь расчета _∆rG⁰₂₉₈ - по стандартным энергиям Гиббса образования исходных веществ и продуктов реакции _∆fG⁰₂₉₈;

_∆rG⁰₂₉₈ = 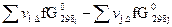(1.73)

Стандартной энергией Гиббса образования вещества _∆fG⁰₂₉₈ называется изменение энергии Гиббса в реакции образования одного моля данного соединения из простых веществ, находящихся в термодинамически устойчивых модификациях, проведенной в стандартных термодинамических условиях.

Если в таблице нет значения _∆fG⁰₂₉₈ для какого-либо сложного вещества, его можно вычислить по уравнению

_∆fG⁰₂₉₈ = _∆fН⁰₂₉₈ – 298 _∆fS⁰₂₉₈; (1.74)

где _∆fН⁰₂₉₈ и _∆fS⁰₂₉₈ – стандартные изменения энтальпии и энтропии соответственно в реакции образования одного моля этого соединения из простых веществ, находящихся в термодинамически устойчивых состояниях, проведенной в стандартных термодинамических условиях.