Вывод кинетического уравнения каталитической реакции на примере гомогенно-каталитического разложения пероксида водорода

Гомогенно-каталитический распад Н2О2 в присутствии ионов Сr2О7 2- . Разложение перекиси водорода в растворе под действием ионов Сr2О7 2- про- исходит в две стадии. В первой стадии реакции обратимо образуется промежуточное соединение:

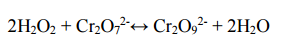
Далее оно необратимо распадается с выделением кислорода и исходного иона Сr2О7 2- . Полагая, что лимитирующей стадией процесса является относительно медленный распад промежуточного соединения, общую скорость процесса можно считать пропорциональной концентрации промежуточного вещества:

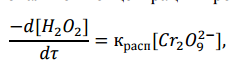
где красп– константа скорости распада промежуточного вещества (𝐶𝑟2𝑂9 2− ). Концентрацию промежуточного вещества можно найти, используя константу равновесия первой стадии:

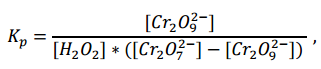
где [Cr2O7 2- ] – исходная концентрация катализатора; ([Cr2O7 2- ] – [Cr2O9 2- ]) – концентрация катализатора при равновесии. Вода находится в большом избытке, и ее концентрацию можно считать постоянной.

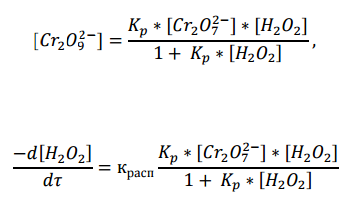
Из последнего уравнения следует, во-первых, что скорость процесса пропорциональна начальной концентрации катализатора и, во- вторых, что в общем случае порядок реакции дробный и может изменяться от 0-го до 2-го. Действительно, если равновесие сдвинуть в сторону образования промежуточного продукта, т.е. Kp[H2O2]>> 1, то порядок реакции равен нулевому по исходному веществу:

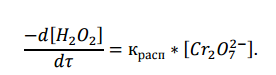
Когда Kp[H2O2] < т.е. равновесие сдвинуто в сторону исходного вещества и порядок реакции будет равен 2.

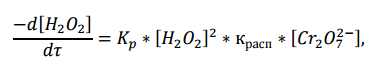
Поскольку сдвиг равновесия в ту или иную сторону зависит от температуры, то и порядок реакции изменяется с температурой. Уравнение (2) можно преобразовать в линейную форму, взяв обратное значение скорости:

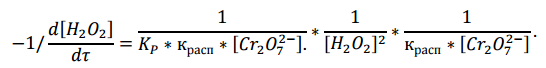
Таким образом, из кинетического опыта можно определить константу равновесия и константу скорости реакции.
Гетерогенно-каталитический распад Н2О2 на активированном угле. Реакция разложения Н2О2 на активированном угле идет большей частью по первому или близкому к первому (0,7–1,2) порядку. Поэтому для оценки скорости реакции можно пользоваться кинетическим уравнением первого порядка:

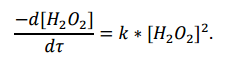
Так как изменение концентрации Н2О2 прямо пропорционально количеству выделяющегося кислорода, то при геометрическом измерении скорости реакции константу скорости удобнее определить через объем выделившегося О2:

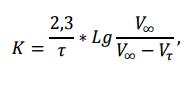
12) Ферментативный катализ. Применение квазиравновесного приближения к выводу уравнения Михаэлис-Ментен. Определение максимальной скорости реакции и константы Михаэлиса.

Ферменты - это белковые молекулы, которые катализируют химические реакции в биологических системах. Их часто называют биологическими катализаторами или биокатализаторами. Без их действия большинство биохимических реакций протекало бы слишком медленно, что препятствовало бы нормальному функционированию живого организма.
Ферменты обладают целым рядом специфических свойств и характеристик:
Размер. Селективность. Эффективность. Зависимость от температуры, отрН среды,от количества и концетрации субстрата.

Действие ферментов заключается в образовании комплекса с молекулой субстрата, которое представляет собой обратимый процесс. Комплекс фермент-субстрат соответствует промежуточному соединению или переходному состоянию в теории промежуточных соединений. Затем этот комплекс распадается и регенерирует фермент. Этот процесс описывается уравнением Михаэлиса - Ментена

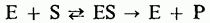
(где Е - фермент, S - субстрат, ES – комплекс)

Согласно существующим воззрениям, молекула субстрата связывается с областью на поверхности фермента, которая называется активным центром. Активность этого центра повышается в присутствии витаминов и некоторых минеральных веществ. За активность ферментов особенно ответственны Активность некоторых ферментов очень зависит от наличия коферментов. Коферментами являются относительно небольшие органические молекулы, которые связываются с активными центрами фермента.
Роль таких коферментов часто выполняют витамины группы В.

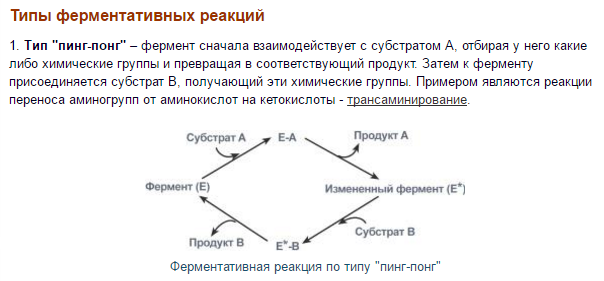
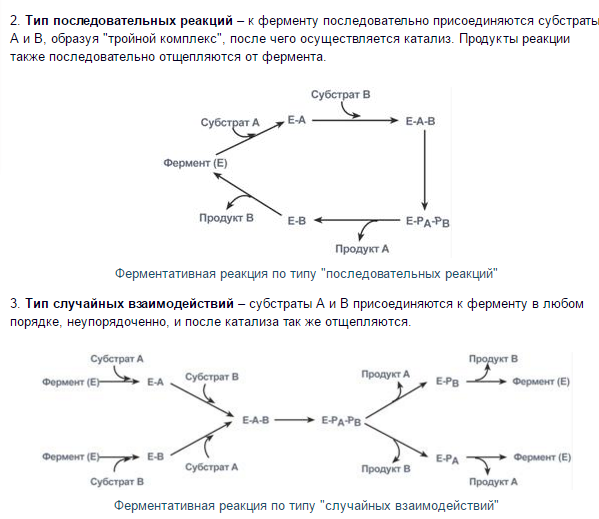
Применение квазиравновесного приближения позволяет выразить скорость образования продукта через начальную концентрацию фермента и текущую концентрацию субстрата:

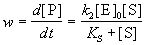
Чаще всего для анализа кинетических схем ферментативного катализа используют метод стационарных концентраций (k2 >> k1). Применение этого метода к простейшей схеме катализа дает уравнение Михаэлиса-Ментен:

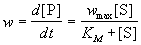
где wmax = k2. [E]0 - максимальная скорость реакции (при бесконечно большой концентрации субстрата),

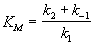
Км- константа Михаэлиса. Эта константа равна концентрации субстрата, при которой скорость реакции равна половине максимальной скорости.