Определение теплоёмкости твёрдых тел. Проверка закона Дюлонга и Пти

Лабораторная работа № 36

1. Цель работы: закрепление теоретических знаний по теме 5.8. “Атомы и молекулы в квантовой физике”

приобретение практических навыков в решении задач по указанной теме

изучение методики расчетов

2. Порядок подготовки к выполнению работы: изучить тему и материал лабораторной работы

3. Порядок выполнения лабораторной работы

4. Подведение итогов выполнения работы

предъявить результаты, подготовка и оформление отчета, заполнить таблички, произвести обработку результатов измерений

5. техника безопасности при выполнении лабораторной работы

Цель работы: определить молярную теплоёмкость твёрдого тела. Проверить закон Дюлонга и Пти.

Теория

Теплоемкость кристаллов. Теория Эйнштейна.

Согласно классическим представлениям кристалл, состоящий из N атомов, является системой с 3N колебательными степенями свободы, на каждую из которых приходится в среднем энергия kT (½ kT в виде кинетической и ½ kT в виде потенциальной энергии). Из этих представлений вытекает закон Дюлонга и Пти, который утверждает, что молярная теплоемкость всех химически простых тел в кристаллическом состоянии одинакова и равна 3R. Этот закон выполняется достаточно хорошо только при сравнительно высоких температурах. При низких температурах теплоемкость кристаллов убывает, стремясь к нулю при приближении к 0К.

Значение kT для средней энергии колебательного движения получается в предположении, что энергия гармонического осциллятора может принимать непрерывный ряд значений. Ранее мы установили, что колебательная энергия квантуется. Это приводит к тому, что средняя энергия колебания оказывается отличной от kT. Согласно формуле ( ) энергия гармонического осциллятора может иметь значения:

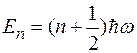(n=0,1,2…).

Приняв, что распределение осцилляторов по состояниям с различной энергией подчиняется закону Больцмана, можно найти среднее значение энергии гармонического осциллятора < ε >. Проделав выкладки, анологичные тем, которые привели нас к формуле ( ), получим для < ε > выражение, отличающееся от ( ) лишь тем, что оно имеет дополнительное слагаемое ½ ħω. Таким образом:

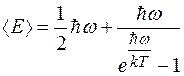
Теория теплоемкости кристаллических тел, учитывающая квантование колебательной энергии, была создана Эйнштейном (1907) и впоследствии усовершенствована Дебаем (1912).

Эйнштейн отождествил кристаллическую решетку из N атомов с системой 3N независимых гармонических осцилляторов с одинаковой собственной частотой ω. Существование нулевой энергии колебаний было установлено значительно позже, лишь после создания квантовой механики. Поэтому Эйнштейн исходил из планкового значения энергии гармонического осциллятора 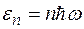. Соответственно в использованном Эйнштейном выражении для < ε > слагаемое ½ ħω отсутствовало.

Умножив второе слагаемое выражения ( ) на 3N, Эйнштейн получил для внутренней энергии кристалла формулу

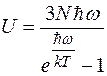
Продифференцировав выражение ( ) по температуре, Эйнштейн нашел теплоемкость кристалла:

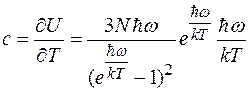
Величина T_θ = 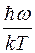называется характеристической температурой.

Рассмотрим два предельных случая.

1. Высокие температуры (kT>> 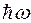). В этом случае можно положить 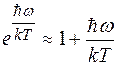в знаменателе и 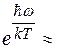1 – в этом числителе формулы ( ). В результате для теплоемкости получается значение

с = 3Nk

Таким образом, мы пришли к закону Дюлонга и Пти.

2. Низкие температуры (kT<< 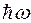). При этом условии единицей в знаменателе выражения ( ) можно пренебречь. Тогда формула для теплоемкости принимает вид

.

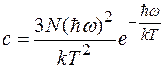Экспоненциальный множитель изменяется значительно быстрее, чем T². Поэтому при приближении к абсолютному нулю выражение ( ) будет стремиться к нулю практически по экспоненциальному закону. Опыт показывает, что теплоемкость кристаллов изменяется вблизи абсолютного нуля не экспоненциально, а по закону T³. Следовательно, теория Эйнштейна дает лишь качественно правильный ход теплоемкости при низких температурах. Количественного согласия с опытом удалось достигнуть Дебаю.

В классической физике теория теплоемкости основывается на законе равнораспределения энергии по степеням свободы. Однородное твердое тело рассматривается как система независимых друг от друга частиц, имеющих три степени свободы и совершающих тепловые колебания с одинаковой частотой. Средняя энергия, приходящаяся на одну колебательную степень свободы равна kT. Тогда внутренняя энергия одного моля твердого тела равна U = 3 N_А <W> = 3 N_А kT . В одном моле N = N_А. Отсюда с учетом того, что k N_А = R. имеем молярную теплоемкость химически простых кристаллических твердых тел

С_μ = 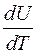= 3R = 25 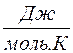= 5,97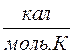

Эта теплоемкость для всех тел одинакова и не зависит от температуры или каких-либо иных характеристик этих тел. Особенно отчетливо зависимость теплоемкости от температуры обнаруживается в низкотемпературных экспериментах, корда классический закон равнораспределения энергий становится абсолютно непригодным

Это и есть закон Дюлонга и Пти.

Упражнение 1.

Оборудование: набор тел примерно одного объема из алюминия, стали, свинца, железа, вольфрама. Термостат. Электроплитка. Сосуд для кипячения воды. Секундомер, весы, штангенциркуль.

Порядок выполнения работы:

1. Определяем массу и теплоёмкость термостата. Для этого заливаем в термостат кипящую воду и через 2 мин. определяем установившуюся температуру.

m_вс_в(tº_к - tº_н) = m_тс_т(tº_к,т - tº_н,т)

m_в - масса залитой воды

с_в - удельная теплоёмкость воды

tº_к - конечная (через 2 мин.)

tº_н - 100ºС

m_т - масса термостата

с_т - удельная теплоёмкость термостата

tº_к,т = tº_к – конечная температура термостата

tº_н,т – комнатная температура

2. Охлаждаем термостат. Кладём в него испытуемый металлический образец и повторяем опыт. Теперь

m_вс_в(tº_к2 - tº_н) = m_Аlс_Al(tº_к,т2 - tº_н,т) + m_тс_т(tº_к,т2 - tº_н,т)

Из ( ) находим m_тс_т и подставляем в ( ). Из ( ) после этого находим теплоёмкость образца из металла.

Используем связь между молярной и удельной теплоёмкостью.

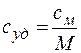
и определяем молярную теплоёмкость с_м.

При выполнении работы в остывший термостат следует заливать каждый раз одинаковое количество кипящей воды при одинаковой температуре. Время установления теплового равновесия в термостате порядка двух минут. При изменениях в конструкции термостата его следует определять экспериментально заново. В опыте по пункту (1), фиксируя конечную температуру от времени τ и строя график tº, С.

Время t_u – постоянная времени термостата и есть время установления теплового равновесия в термостате.

Данные эксперимента занести в таблицу

№ образца	Начальная темпера тура воды	Количес твенная темпера тура tºн	Масса залитой воды	Масса образца mAl	tºк, температура установившаяся в калориметре	Суд	См

Упражнение 2.

Определение удельной теплоемкости металлов методом охлаждения

Оборудование: электропечь, набор образцов для исследования, секундомер, термопара, гальванометр, технические весы.

Введение

Всякое тело, которое имеет температуру выше температуры окружающей среды, будет охлаждаться, причем скорость охлаждения зависит от теплоемкости тела. Если взять два металлических стержня определенной формы, то, сравнивая кривые охлаждения (температуры как функции времени) этих образцов, один из которых служит эталоном (его удельная теплоемкость известна), можно определить теплоемкость другого образца, если определить скорость охлаждения.

Количество теплоты, теряемое элементарным объемом dV металла за время dt,

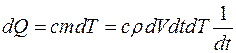(1)

где с – удельная теплоемкость металла; r - его плотность; Т – температура образца (принимается одинаковой во всех точках образца, поскольку линейные размеры тела малы, а теплопроводность металла большая).

Значение dQ можно подсчитать, кроме того, по закону Ньютона:

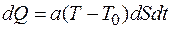, (2)

где а – коэффициент теплоотдачи; 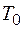- температура окружающей среды; dS – элемент поверхности.

Сравнивая формулы (1) и (2), получаем:

.

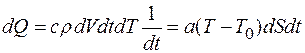Общее количество теплоты, которое теряет весь объем образца,

.

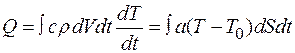Считая, что 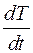, с и r не зависят от координат точек объема, а а ,Т, 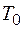- от координат точек поверхности образца, можно записать:

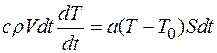, (3)

где V – объем образца; S – площадь его поверхности.

Запишем выражение (3) для двух образцов одинаковой формы и размеров, но из разных металлов 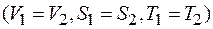. В этом случае их коэффициенты теплоотдачи будут одинаковы .

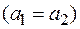Разделив одно выражение на другое, после простых преобразований получим:

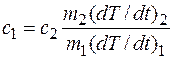, (4)

где 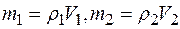- массы соответственно первого и второго образцов.

Описание установки

Определение удельной теплоемкости металла производится на установке, схема которой приведена ниже.

Цилиндрическая электропечь 2 смонтирована на штативе 1, вдоль которого она может перемещаться вверх или вниз. Образец 3 представляет собой цилиндр с высверленным с одной стороны каналом. В этот канал помещают фарфоровую трубку с вмонтированной в нее термопарой 4. Температура образца определяется по гальванометру 5 с помощью градуировочного графика.

Порядок выполнения работы

1. Поместите внутрь образца фарфоровую трубку с термопарой.

2. Поднимите столик с образцом по направляющему стержню настолько, чтобы образец оказался внутри печи.

3. Включите печь в электрическую сеть.

4. Нагрев образец до температуры 250…300°С (определите для этого число делений шкалы гальванометра по графику), опустите образец, отключите электропечь.

5. Нагретый образец будет охлаждаться в неподвижном воздухе. Через каждые 10 с записывайте температуру Т образца по показаниям гальванометра. Время t отсчитывайте по секундомеру.

6. По полученным данным постройте для каждого образца кривые охлаждения, т.е. график Т = f(t) зависимости температуры образца от времени t, откладывая время по оси абсцисс, а температуру – по оси ординат.

7. Постройте графики зависимости скорости охлаждения ΔТ/Δt образца от температуры Т, т.е. ΔТ/Δt = f(Т). Для этого выберите на оси ординат графика Т=f(t) некоторые значения температур образца (например, 100°, 150°, 200°, и т. д.). Вблизи каждого значения температуры выберите небольшие одинаковые интервалы температур ΔТ. Из полученных точек проведите перпендикуляры к оси ординат так, чтобы они пересекались с графиком кривой охлаждения. Из этих точек пересечения проведите перпендикуляры на ось абсцисс. В результате на оси абсцисс получится ряд интервалов времени Δt₁, Δt_2, Δt₃,_… , на протяжении которых образец при соответствующих Т₁, Т₂, Т₃,… охлаждается на ΔТ. Отношения ΔТ₁/ Δt₁, ΔТ₂/ Δt₂, ΔТ₃/ Δt₃, характеризуют скорость охлаждения образцов при температурах Т₁, Т₂, Т₃,… . Получите числовые значения отношений ΔТ/ Δt для каждой выбранной температуры Т и результаты занесите в таблицу. Постройте графики зависимости ΔТ/Δt=f(T) для медного и железного образцов, откладывая по оси абсцисс значения температур Т, а по оси ординат- отношения ΔТ/Δt.

8. Определите теплоёмкость железа для температур 100°, 150°, 200°, 250°. Для этого в формулу (4) подставьте отношение ΔТ/Δt для каждого образца при этих температурах. За эталонный примите медный образец. Зависимость удельной теплоёмкости меди от температуры известна. Из прил. 20 возьмите значение теплоёмкости меди для соответствующих температур и подставьте в формулу (4). Массы m₁ и m₂ образцов определите взвешиванием.

Контрольные вопросы и задания.

1. Что называется теплоёмкостью и удельной теплоёмкостью?

2. Назовите единицы теплоёмкости и удельной теплоёмкости.

3. Каким образом можно подсчитать количество теплоты, полученное телом при нагревании?

4. Как рассчитать количество теплоты, отдаваемое телом через боковую поверхность при остывании?

5. При каких условиях коэффициенты теплоотдачи двух образцов будут одинаковыми?

6. Каким образом в данной работе определяется температура образцов?

7. При каких температурах скорость охлаждения образцов выше - при низких или высоких?

8. В чём заключается суть определения теплоёмкости металлов методом охлаждения?

9. Каким образом изменяется теплоемкость твердых тел при высоких и при низких температурах по теории Эйнштейна и Дебая.

10. Дайте определение теплоемкости тела, удельной теплоемкости и молярной теплоемкости вещества.

11. Можно ли понятие теплоемкости перенести на изучение?

12. Что понимают под степенью свободы микрочастиц в кристалле?

13. Какими процессами определяются теплопотери в калориметре?

14. Почему калориметр должен быть металлическим и иметь хорошую теплоизоляцию?