Наиболее вероятная энергия

При наиболее вероятной энергии функция распределения максимальна

.

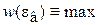Из

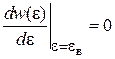
с учетом (2.48а)

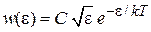находим наиболее вероятную энергию

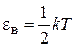. (2.49)

Средняя энергия

Для средней энергии с учетом (2.42а)

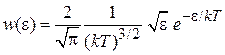
получаем

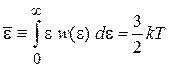, (2.50)

что согласуется с теоремой (2.39) о распределении кинетической энергии по степеням свободы. При 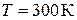находим .

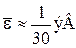Доказательство (2.50)

Вычисляем

,

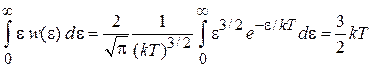где использовано

,

, , .

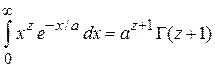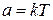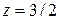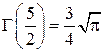Поток частиц

Плотность потока частиц 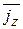по оси z есть среднее число частиц, проходящих за 1с через единичную площадку, перпендикулярную оси z. Независимые движения по x и y не влияют на результат, поэтому считаем эти скорости нулевыми.

Пусть в начальный момент частицы со скоростями в интервале 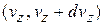заполняют цилиндр с образующей длиной 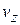, параллельной оси z. Площадь основания цилиндра единица. Концентрация частиц 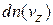. Через 1с все эти частицы пересекут правый торец цилиндра и выйдут из него. Их число равно произведению объема цилиндра на концентрацию частиц

.

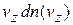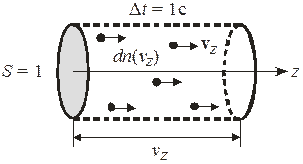
Суммируем по всем значениям скорости с положительной проекцией и получаем плотность потока частиц

.

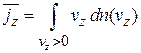Используем (2.42а)

,

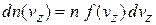где функция распределения

,

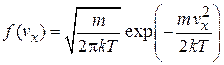тогда

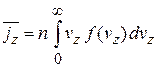. (2.51)

Вычисляем интеграл

,

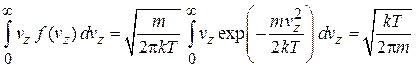где использовано

,

, , .

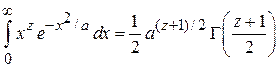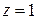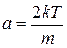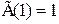Получаем

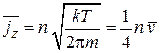(2.52)

– плотность потока частиц, движущихся в положительную сторону оси z, или число соударений частиц со стенкой единичной площади за 1 с, где использована средняя скорость (2.46)

.

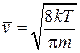Такой же поток (2.52) идет в обратную сторону, а также в любом направлении внутри объема с газом. Чем выше температура и концентрация, тем больше плотность потока частиц.

Если каждая частица имеет заряд e, то их движение в определенном направлении создает электрический ток, плотность тока

.

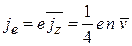Результирующий ток отсутствует из-за равноправия всех направлений.

Поток импульса

Плотность потока импульса 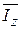по оси z есть средний импульс, переносимый за 1с через единичную площадку, перпендикулярную оси z. Рассматриваемое число частиц со скоростями в интервале 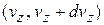равно

.

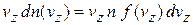Частица несет импульс 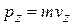. Общий импульс

.

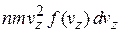Суммируем по всем значениям скорости и получаем

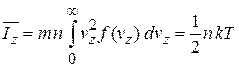. (2.53)

Доказательство

,

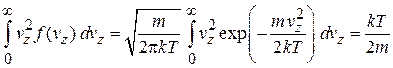где использовано

,

,

, , .

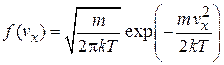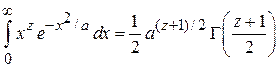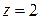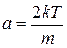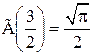Если стенка поглощает падающие на нее частицы, то импульс частиц передается стенке. Переданный импульс за единицу времени равен действующей силе. Если импульс получает единица площади стенки, то сила равна давлению на стенку. Следовательно, стенка, поглощающая частицы, испытывает давление

.

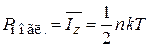Если стенка упруго отражает падающие на нее частицы, то давление на нее удваивается

.

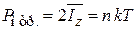Полученное равенство является уравнением идеального газа.

Поток энергии

Плотность потока энергии 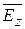по оси z есть средняя энергия, переносимая за 1с через единичную площадку, перпендикулярную оси z. Частица несет энергию, связанную с движением по трем направлениям:

.

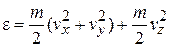Для потока вдоль оси z оси x и y равноправны, тогда

.

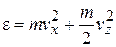Число частиц, проходящихза 1с через единичную площадку, перпендикулярную оси z, со скоростями в интервале 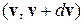равно

,

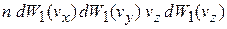где 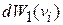– вероятность найти частицу с проекцией скорости на ось i в интервале значений 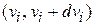. Умножаем на энергию, суммируем по всем возможным проекциям, и получаем плотность потока энергии

.

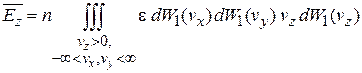Подставляем

,

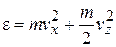находим

.

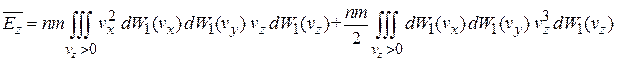Интегралы разделяются

.

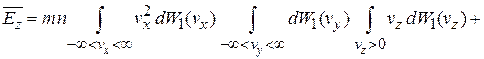
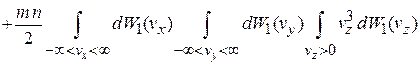Учитываем нормировку вероятности

, ,

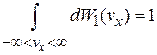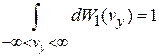получаем

.

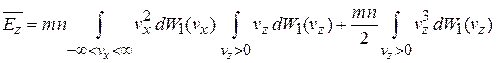Для вычисления интегралов используем (2.42)

,

,

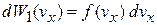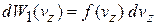выражение (2.51) для плотности потока частиц

,

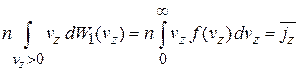и выражение (2.42б) для среднеквадратичной проекции скорости

.

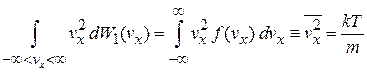В результате

.

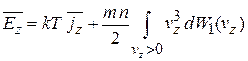Ищем

,

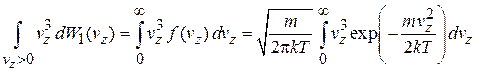где учтено

.

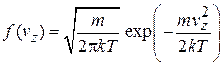Используем

,

, , ,

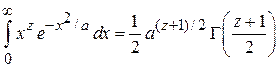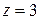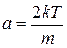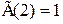тогда

.

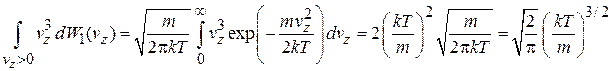С учетом

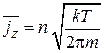
находим

.

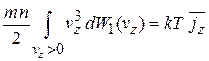В результате плотность потока энергии

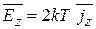. (2.54)

Следовательно, средняя энергия частицы в потоке

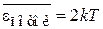. (2.54а)

Это превышает среднюю энергию частицы в газе (2.50)

.

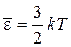Поток не является равновесным состоянием, к нему не применима теорема о распределении энергии по степеням свободы. Бóльший вклад вносят в поток более быстрые частицы.