Основные кинетические величины
Закон действующих масс
aA + bB → cC + dD
V = k·c 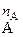 ·c
·c 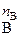 ,
,
где k – константа скорости.
Правило Вант-Гоффа
V 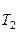 = V
= V 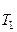 · γ
· γ 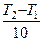 ; k
; k 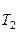 = k
= k 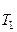 · γ
· γ 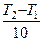 ,
,
где γ – температурный коэффициент.
Уравнение Аррениуса
k = A· e 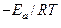 ,
,
где А – предэкспоненциальный множитель; Еа – энергия активации;
lg k = lg A – 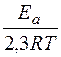 ;
;
lg 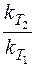 = –
= – 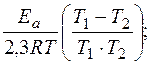 lg
lg 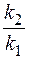 = –
= – 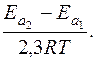
Константа равновесия
аА + bB 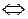 cC + dD
cC + dD
Kc = 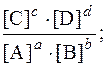 Kp =
Kp = 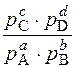 , где р – парциальное давление;
, где р – парциальное давление;
Kp = Kc(RT)Δυ ; Δυ = (c + d) – (a + b);
ΔG 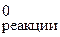 = –2,3 RT lg Kравн.
= –2,3 RT lg Kравн.
Кинетические уравнения реакций
0-го порядка: 1 – 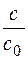 =
= 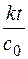 , где t – время;
, где t – время;
1-го порядка: с = с0·е–kt ; lnc = lnc0 – kt ;
2-го порядка: 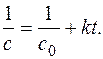
Решение типовых задач
Пример 4.1.Построить кинетическую кривую расходования вещества А и определить графически начальную скорость (V0), порядок реакции (n) и константу скорости (k) реакции.
Т а б л и ц а 4.1
| Время, с | |||||
| с·10-3, моль/л | 17,8 | 10,6 | 7,1 | 5,4 | 4,6 |
Р е ш е н и е
1) Строим кинетическую кривую расходования вещества А в координатах «концентрация – время» (рис. 4.1), проводим касатель-ную к начальному участку кривой и определяем начальную скорость реакции
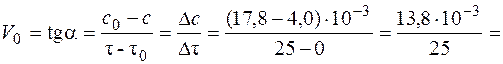
= 0,000552 моль/л·с = 5,52·10-4 моль/л·с.

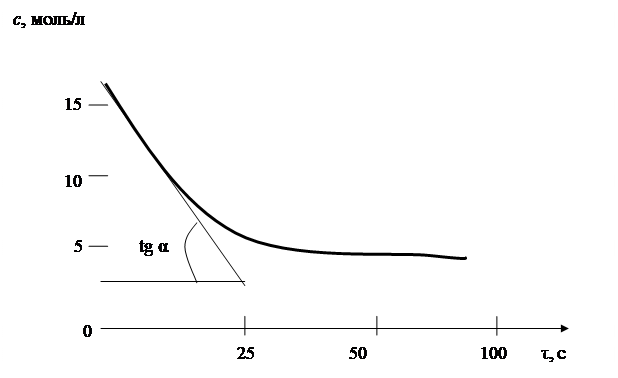
Рис. 4.1. Кинетическая кривая расходования вещества А
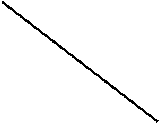
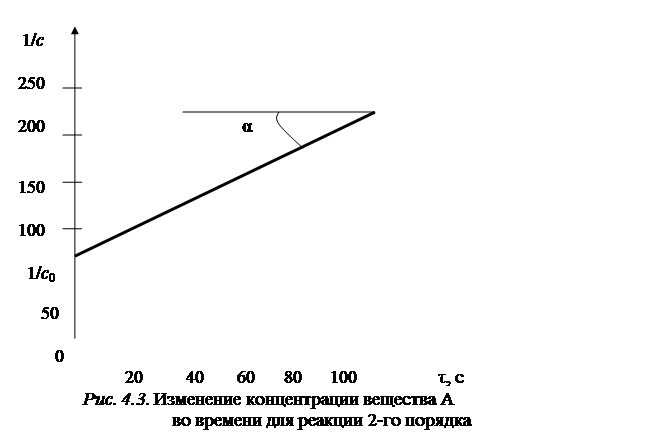
2) Находим порядок реакции (n) и константу скорости (k) по кинетической кривой расходования вещества А. Для этого спрямляем кинетическую кривую в координатах «ln c – τ» (для реакции 1-го порядка) (рис. 4.2) или в координатах «1/c – τ» (для реакции 2-го порядка) (рис. 4.3).
Т а б л и ц а 4.2
| ln c | 2,9 | 2,4 | 2,0 | 1,7 | 1,5 |
| 1/c, л/моль | 56,2 | 94,3 | 140,8 | 185,2 | 217,4 |
| τ, с |
 |
ln c
 3,5
3,5
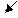

 3,0
3,0
lnc0
 2,5
2,5
2,0

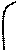 tg α
tg α
 1,5
1,5
 |
 1,0
1,0
 0,5
0,5





 0
0
20 40 60 80 100 τ, c
Рис. 4.2 . Изменение концентрации вещества А
во времени для реакции 1-го порядка
 |
 | |||
 |
Рис. 4.2 б. Изменение концентрации вещества А
Для реакции 1-го порядка
ln c = ln c0 – k·τ; k = 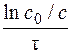 .
.
Отрезок, отсекаемый на оси ординат – ln c0, а tg α = k. Как видно из рис. 4.2, реакция расходования вещества А не является реакцией 1-го порядка.
Для реакции 2-го порядка
1/c = 1/c0 + kτ.
Отрезок, отсекаемый на оси ординат – 1/c0, tg α = 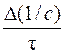 .
.
k = 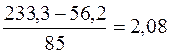 л/моль·с.
л/моль·с.
Как видно из рис. 4.3, реакция расходования вещества А является реакцией 2-го порядка.
Таким образом V0 = 5,52·10-4 моль/л·с; k = 2,08 л/моль·с.
Пример 4.2.Вычислить графически энергию активации (ЕА) и предэкспоненциальный множитель А по значениям констант скоростей реакций k1 и k2 при температурах Т1 и Т2, записать в аналитической форме зависимость константы скорости от температуры и рассчитать константу скорости k3 при температуре Т3 для реакции
2 HI → H2 + I2.
Т а б л и ц а 4.3
| Т1, К | k1, л/моль·с | Т2, К | k2, л/моль·с | Т3, К |
| 3,11·10-7 | 1,18·10-6 |
Р е ш е н и е
Вычисляем энергию активации (ЕА) и предэкспоненциальный множитель, строя зависимость в координатах «ln k – 1/T».
Исходя из уравнения Вант-Гоффа-Аррениуса
ln k = ln A – 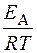 ,
,
отрезок, отсекаемый на оси ординат – ln A, а tg α = 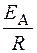 (рис. 4.4).
(рис. 4.4).
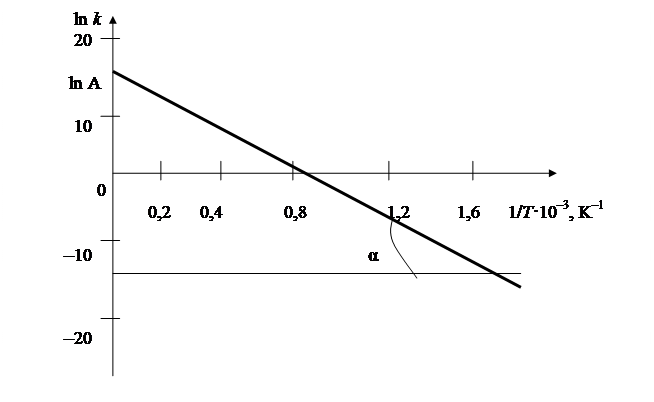
Рис. 4.4. Зависимость константы скорости реакции
от температуры
Т а б л и ц а 4.4
| k·107 | 3,11 | 11,8 |
| ln k | -14,98 | -13,65 |
| T, K | ||
| 1/T·10-3, K-1 | 1,80 | 1,74 |
По графику определяем: ln A = 16,5; A = 14,7·106.
tg α = EA/R = 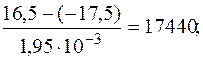
EA = 17440·R = 17440·8,31 Дж/моль = 144926 Дж/моль =
= 144,9 кДж/моль.
Для реакции 2 HI → H2 + I2 предэкспоненциальный множитель А = 14,7·106 и энергия активации ЕА = 144,9 кДж/моль.
Аналитическая форма зависимости константы скорости от температуры будет иметь вид
ln A = ln 14,7·106 - 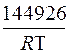
и ln k3 = ln 14,7·106 - 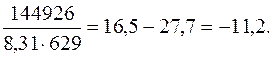
Тогда k3 = 1,37·10-5 л/моль·с.
Пример 4.3.Определить порядок и молекулярность реакции. Написать выражение для определения скорости реакции:
а) Н2 (г) + S (к) = Н2S (г);
б) С2Н6 (г) = Н2 (г) + С2Н4 (г);
в) Н2 (г) + О2 (г) = 2Н2О (ж);
г) СаСО3 (тв) = СаО (тв) + СО2 (г);
д) Fe (тв) + S (тв) = FeS (тв).
Р е ш е н и е
Порядок реакции определяется суммой величин показателей степени при значениях концентраций исходных веществ в кинетическом уравнении:
а) V1 = k1 [H2] – реакция 1-го порядка;
б) V2 = k2 [C2H6] – реакция 1-го порядка;
в) V3 = k3 [H2][O2] – реакция 2-го порядка;
г) V4 = k4 – реакция 0-го порядка;
д) V5 = k5 – реакция 0-го порядка.
Молекулярность реакции определяется числом молекул, одно-временным взаимодействием которых осуществляется акт химичес-кого взаимодействия.
а), в), д) – реакции двухмолекулярные;
б), г) – реакции одномолекулярные.
Выражения для определения скорости:
реакция 0-го порядка: V = – 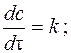
реакция 1-го порядка: V = – 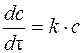 ;
;
реакция 2-го порядка: V = k·c1·c2; V = k·c2 (c1 = c2).
Пример 4.4.а) Вычислить, во сколько раз увеличивается (уменьшается) скорость химической реакции при повышении температуры Δt = 70 оС и γ = 2.
б) При температуре 20 оС реакция заканчивается за 24 мин (γ = = 2). Определить время протекания реакции при температуре 50 оС.
в) На сколько градусов надо повысить температуру, чтобы скорость реакции возросла в 32 раза при γ = 2.
Р е ш е н и е
а) 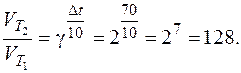 Скорость реакции увеличивается в 128 раз.
Скорость реакции увеличивается в 128 раз.
б) V50 = V20·γ 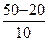 = V20·23 = 8V20.
= V20·23 = 8V20.
Таким образом, скорость реакции при повышении температуры от 20 до 50 оС увеличивается в 8 раз, а следовательно для проведения реакции потребуется в 8 раз меньше времени, т.е. 24 мин : 8 = 3 мин.
в) 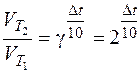 = 32. ln 2
= 32. ln 2 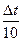 = ln 32.
= ln 32.
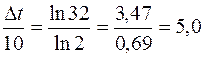 ; Δt = 5·10 = 50 оС.
; Δt = 5·10 = 50 оС.
Таким образом, чтобы скорость реакции возросла в 32 раза при γ = 2, необходимо повысить температуру на 50 градусов.
Пример 4.5. Написать выражение и вычислить константу равновесия (Кс) обратимой реакции Х (г) + 3Y (г) 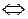 2 Z (г), если равновесная концентрация сZ = 0,2 моль/л, а исходные концентрации сX = 0,5 моль/л и сY = 0,8 моль/л. Определить, в какую сторону сместится равновесие при повышении температуры (ΔН > 0) и как изменятся скорости прямой и обратной реакций, если объем газовой смеси увеличить в 2 раза.
2 Z (г), если равновесная концентрация сZ = 0,2 моль/л, а исходные концентрации сX = 0,5 моль/л и сY = 0,8 моль/л. Определить, в какую сторону сместится равновесие при повышении температуры (ΔН > 0) и как изменятся скорости прямой и обратной реакций, если объем газовой смеси увеличить в 2 раза.
Р е ш е н и е
1) Составим схему:
Уравнение реакции Х (г) + 3Y (г) 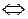 2 Z (г);
2 Z (г);
Исходные концентрации: 0,5 0,8 0
Прореагировало А В -
Равновесные концентрации Б Г 0,2
По уравнению реакции 1 моль Х дает 2 моль Z, следовательно, для 0,2 моль Z нужно 0,1 моль Х, т.е. А = 0,1 моль. Рассчитываем Б = = 0,5 – А = 0,5 – 0,1 = 0,4 моль/л.
Если 3Y переходят в 2Z, то для образования 0,2 моль Z нужно 0,3 моль Y, т.е. В = 0,3 моль. Определяем Г = 0,8 – В = 0,8 – 0,3 = = 0,5 моль/л.
С помощью равновесных концентраций определяем константу равновесия
Кс = с 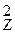 /сХ·с
/сХ·с 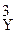 = 0,22/0,4·0,53 = 0,8.
= 0,22/0,4·0,53 = 0,8.
2) Так как ΔН > 0, то данная реакция является эндотермической и при повышении температуры равновесие сместится вправо.
3) Запишем выражение для скорости прямой реакции до изменения объема газовой смеси
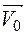 =
= 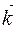 (сХ)0·(сY)
(сХ)0·(сY) 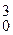 .
.
Увеличение объема газовой смеси в 2 раза равносильно уменьшению давления и концентрации в 2 раза:
cX = ½ (cX)0; cY = ½ (cY)0.
Тогда скорость реакции после изменения объема газовой смеси будет определяться следующим выражением
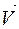 =
= 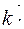 ½ (cX)0·(½ (cY)0)3 = 1/16
½ (cX)0·(½ (cY)0)3 = 1/16 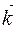 (сX)0 (cY)
(сX)0 (cY) 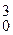 ,
,
скорость прямой реакции уменьшится в 16 раз.
Скорость обратной реакции определяется формулой
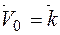 (сZ)
(сZ) 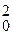 .
.
Если сZ = ½ (cZ)0, то
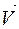 =
= 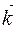 (½ (cZ)0)2 = ¼
(½ (cZ)0)2 = ¼ 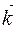 (cZ)
(cZ) 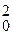 ,
,
скорость обратной реакции уменьшится в 4 раза.
Таким образом, при увеличении объема газовой смеси в 2 раза, скорость прямой реакции уменьшается в 16 раз, а обратной в 4 раза.
В целом равновесие данной обратимой реакции сместится влево.
Задачи
4.1. Постройте кинетическую кривую расходования вещества А и определите графически начальную скорость (V0), порядок (n) и константу скорости (k) для реакции вашего варианта (табл. 4.5, 4.6).
Т а б л и ц а 4.5
| Вариант | [A] = f (τ) | |||||
| τ·103, с [A], моль/л | 5,000 | 1,0 4,950 | 2,5 4,877 | 4,0 4,804 | 5,5 4,732 | |
| τ·105, с [A], моль/л | 5,000 | 0,4 4,980 | 1,0 4,950 | 1,6 4,921 | 1,9 4,907 | |
| τ·104, с [A], моль/л | 1,000 | 0,5 0,995 | 1,1 0,989 | 2,0 0,980 | 5,0 0,951 | |
| τ·103, с [A], моль/л | 5,000 | 0,4 4,808 | 0,7 4,673 | 1,0 4,545 | 1,6 4,310 | |
| τ·103, с [A], моль/л | 5,000 | 4,980 | 4,965 | 4,950 | 4,921 | |
| Окончание табл. 4.1 | ||||||
| τ, с [A], моль/л | 5,000 | 0,03 4,985 | 0,06 4,970 | 0,09 4,955 | 0,12 4,940 | |
| τ, с [A], моль/л | 1,000 | 0,4 0,992 | 0,7 0,986 | 1,0 0,980 | 1,6 0,969 | |
| τ, с [A], моль/л | 5,000 | 0,9 4,955 | 1,5 4,926 | 3,0 4,852 | 4,5 4,780 | |
| τ·102, с [A], моль/л | 5,000 | 0,4 4,980 | 0,7 4,965 | 1,0 4,950 | 1,3 4,935 | |
| τ·102, с [A], моль/л | 1,00 | 2,4 0,98 | 4,8 0,95 | 7,2 0,93 | 9,0 0,91 | |
| τ, с [A], моль/л | 1,000 | 1,5 0,985 | 3,0 0,970 | 6,0 0,942 | 9,0 0,914 | |
| τ, с [A], моль/л | 1,000 | 0,04 0,996 | 0,07 0,993 | 0,10 0,990 | 0,13 0,987 | |
| τ, с [A], моль/л | 1,000 | 0,4 0,926 | 0,7 0,877 | 1,0 0,833 | 1,3 0,794 | |
| τ, мин [A], моль/л | 56,0 | 55,3 | 54,2 | 52,5 | 49,0 | |
| τ, час [A], моль/л | 0,1214 | 6,6 0,1148 | 19,0 0,1064 | 26,2 0,1020 | 42,8 0,0945 |
Т а б л и ц а 4.6
| Вариант | [A] = f (τ) | |||||
| 1’ | τ·104, с [A], моль/л | 5,000 | 1,0 4,950 | 2,5 4,877 | 4,0 4,804 | 5,5 4,732 |
| 2’ | τ, с [A], моль/л | 5,000 | 0,4 4,808 | 0,7 4,673 | 1,0 4,545 | 1,6 4,310 |
| 3’ | τ·103, с [A], моль/л | 1,000 | 0,3 0,994 | 0,6 0,988 | 1,2 0,977 | 3,0 0,940 |
| 4’ | τ·103, с [A], моль/л | 1,00 | 0,32 0,94 | 0,80 0,86 | 1,07 0,82 | 1,40 0,78 |
| 5’ | τ·103, с [A], моль/л | 1,000 | 0,8 0,992 | 2,0 0,980 | 3,5 0,966 | 5,0 0,951 |
| 6’ | τ, с [A], моль/л | 1,000 | 0,861 | 0,741 | 0,638 | 0,549 |
| 7’ | τ, с [A]·103, моль/л | 10,00 | 0,3 5,83 | 0,6 3,40 | 0,9 1,98 | 1,2 1,15 |
| Окончание табл. 4.6 | ||||||
| 8’ | τ, с [A]·103, моль/л | 10,00 | 0,14 7,56 | 0,28 5,71 | 0,42 4,32 | 0,56 3,26 |
| 9’ | τ, с [A], моль/л | 0,370 | 0,274 | 0,203 | 0,151 | |
| 10’ | τ, мин [A], моль/л | 35,35 | 4,75 30,5 | 10,0 27,0 | 20,0 23,2 | 35,0 20,3 |
| 11’ | τ, мин [A], моль/л | 0,0234 | 0,0193 | 0,0171 | 0,0139 | 0,0130 |
| 12’ | τ, мин [A], моль/л | 16,4 | 15,0 | 13,4 | 12,8 | 11,5 |
| 13’ | τ, с [A], моль/л | 2,000 | 1,527 | 1,165 | 0,890 | 0,679 |
| 14’ | τ·10-2, с [A], моль/л | 4,500 | 1,2 3,140 | 2,4 2,190 | 3,6 1,528 | 4,8 1,066 |
| 15’ | τ·103, с [A]·104, моль/л | 5,000 | 2,5 3,704 | 5,0 2,744 | 7,5 2,033 | 10,0 1,506 |
4.2. Вычислите графически энергию активации (ЕА) и предэкспоненциальный множитель (А) по значениям констант скоростей реакции k1 и k2 при температурах Т1 и Т2; запишите в аналитической форме зависимость константы скорости от температуры: ln k = f (T); рассчитайте константу скорости k3 при температуре Т3 для реакции вашего варианта (табл. 4.7, 4.8).
Т а б л и ц а 4.7
| Вариант | Реакция | Т1,К | k1 | Т2,К | k2 | Т3,К |
| СН3С6Н4N2Cl+H2O→ →CH3C6H4OH+N2+HCl | 9·10-3 мин-1 | 13·10-3 мин-1 | ||||
HBr + O2→ HO 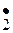 + Br + Br 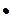 | 5,1 см3/моль·с | 46,2 см3/моль·с | ||||
| CH3COOH → C2H4 + + H2 + CO2 | 2,59·10-2 мин-1 | 3,43·10-2 мин-1 | ||||
| C2H5ONa + CH3I → → C2H5OCH3 + NaI | 0,0336 л/моль·мин | 2,125 л/моль·мин | ||||
| С12Н22О11 + Н2О → С6Н12О6 (глюкоза) + + С6Н12О6 (фруктоза) | 5,03·10-2 мин-1 | 2,1·10-2 мин-1 | ||||
| Окончание табл. 4.7 | ||||||
| N2O5 → N2O4 + ½ O2 | 0,203·102 л/моль·мин | 0,475·10-3 л/моль·мин | ||||
| 2NO → N2 + O2 | 4,76·104 л/моль·мин | 1,07·103 л/моль·мин | ||||
| 2CH2O + NaOH → → HCO2Na + CH3OH | 9,166·10-5 л/моль·с | 4,9·10-3 л/моль·с | ||||
| NaBO3 + H2O → → NaH2BO3 + ½ O2 | 2,2·10-3 мин-1 | 4,1·10-3 мин-1 | ||||
| CH2OHCH2Cl+ KOH→ →CH2OHCH2OH+KCl | 1,13·10-2 л/моль·с | 8,72·10-2 л/моль·с | ||||
| (C2H5)3N + CH3I → → [(C2H5)3CH3N]I | 3,29·10-2 л/моль·с | 8,1·10-2 л/моль·с | ||||
| 2HI → H2 + I2 | 0,942·10-6 л/моль·мин | 0,31·10-2 л/моль·мин | ||||
| H2 + Br2 → 2HBr | 1,59·10-2 л/моль·мин | 2,6·10-3 л/моль·мин | ||||
| (CH3)2SO4 + NaI → → CH3I + Na(CH3)SO4 | 4,83·10-4 л/моль·с | 1,73·10-2 л/моль·с | ||||
| H2 + Br2 → 2HBr | 3,6·10-4 л/моль·мин | 8,6·10-2 л/моль·мин |
Т а б л и ц а 4.8
| Вариант | Реакция | Т1,К | k1 | Т2,К | k2 | Т3,К |
| 1’ | СН3СО2СН3 + Н2О → →СН3СО2Н + СН3ОН | 1,609·10-2 л/(моль·мин) | 3,784·10-2 л/(моль·мин) | |||
| 2’ | НСНО + Н2О2 → → НСООН + Н2О | 0,75 л/(моль·ч) | 0,94 л/(моль·ч) | |||
| 3’ | С6Н5СН2Br+C2H5OH→ →C6H5CH2OC2H5+HBr | 1,44 л/(моль·мин) | 2,01 л/(моль·мин) | |||
| 4’ | H2 + I2 → 2HI | 666,8 | 15,59 см3/(моль·с) | 698,6 | 67,0 см3/(моль·с) | |
| 5’ | 2NO2 → N2 + 2O2 | 6,72 л/(моль·мин) | л/(моль·мин) | |||
| 6’ | СО(СН2СООН)2 → → СО(СН3)2 + 2СО2 | 2,46·10-5 мин-1 | 5,76·10-3 мин-1 | |||
| 7’ | SO2Cl2 → SO2 + Cl2 | 1,02·10-6 л/(моль·с) | 2,2·10-5 л/(моль·с) | |||
| Окончание табл. 4.8 | ||||||
| 8’ | C6H5N2Cl → → C6H5Cl + N2 | 1,8·102 с-1 | 3,2·102 с-1 | |||
| 9’ | 2HI → H2 + I2 | 666,8 | 0,256 см3/(моль·с) | 698,6 | 1,242 см3/(моль·с) | |
| 10’ | CH2ClCOOH+H2O → → CH2OHCOOH+HCl | 0,222·10-4 л/(моль·мин) | 0,237·10-2 л/(моль·мин) | |||
| 11’ | C2H6 → C2H4 + H2 | 2,5·105 с-1 | 141,5·105 с-1 | |||
| 12’ | СН3СО2СН3+Н2О 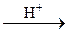 → СН3СО2Н + СН3ОН → СН3СО2Н + СН3ОН | 0,653·10-3 л/(моль·мин) | 1,663·10-3 л/(моль·мин) | |||
| 13’ | Cu + (NH4)2S2O8 → → CuSO4 + (NH4)2SO4 | 9,6·10-3 л/(моль·мин) | 39,96·10-3 л/(моль·мин) | |||
| 14’ | РН3 → Р (г) + 3/2 Н2 | 3,05·10-4 л/(моль·с) | 6,33·10-5 л/(моль·с) | |||
| 15’ | CH3CO2C2H5+NaOH → → CH3CO2Na + C2H5OH | 2,37 л/(моль·мин) | 3,204 л/(моль·мин) |
4.3. Определите порядок и молекулярность реакции для вашего варианта. Напишите выражение для вычисления скорости реакции (табл. 4.9).
Т а б л и ц а 4.9
| Номер варианта | Уравнение реакции |
| СО2 (г) + С (к) = 2 СО (г) | |
| 2 NH3 (г) = N2 (г) + 3 Н2 (г) | |
| СО (г) + Н2 (г) = С (к) + Н2О (г) | |
| SO2 (г) + Cl2 (г) = SO2Cl2 (г) | |
| СН4 (г) + Н2О (г) = СО (г) + 3Н2 (г) | |
| 2 NO (г) + О2 (г) = 2 NO2 (г) | |
| PCl5 (г) = PCl3 (г) + Cl2 (г) | |
| 2NO2 (г) = N2O4 (г) | |
| FeO (к) + CO (г) = Fe (к) + CO2 (г) | |
| 2H2S (г) + SO2 (г) = 3S (к) + 2H2O (г) | |
| С (к) + 2Н2 (г) = СН4 (г) | |
| СН4 (г) + 2Н2О = СО2 (г) + 4Н2 (г) | |
| СО (г) + Н2О (г) = СО2 (г) + Н2 (г) | |
| 2N2 + O2 = 2N2O | |
| SO2 (г) + NO2 (г) = SO3 (г) + NO (г) | |
| 1’ | СН4 (г) + 2О2 (г) = СО2 (г) + 2Н2О (г) |
| Окончание табл. 4.5 | |
| 2’ | CO (г) + Cl2 (г) = СOCl2 (г) |
| 3’ | 2SO2 (г) + O2 (г) = 2SO3 (г) |
| 4’ | С2Н4 (г) + Н2О (г) = С2Н5ОН (г) |
| 5’ | H2 (г) + I2 (г) = 2HI (г) |
| 6’ | CHCl3 (г) + Cl2 (г) = CCl4 (г) + HCl (г) |
| 7’ | С2Н4 (г) + Н2О (г) = С2Н5ОН (г) |
| 8’ | CaO (к) + CO2 (г) = CaCO3 (к) |
| 9’ | Cl2 (г) + 2HI (г) = 2HCl (г) + I2 (г) |
| 10’ | I2 (г) + H2S (г) = 2HI (г) + S (к) |
| 11’ | С2Н4 (г) + Н2 (г) = С2Н6 (г) |
| 12’ | СаО (к) + Н2О (г) = Са(ОН)2 (к) |
| 13’ | 2Ag (к) + Cl2 (г) = 2AgCl (к) |
| 14’ | Mg (к) + 2H2O (г) = Mg(OH)2 (к) + H2 (г) |
| 15’ | CuO (к) + H2 (г) = Cu (к) + Н2О (г) |
4.4.1. Вычислите, во сколько раз увеличивается (уменьшается) скорость химической реакции для вашего варианта при повышении температуры на Δt при данном значении γ (табл. 4.10).
Т а б л и ц а 4.10
| Вариант | Δt | γ | Вариант | Δt | γ |
| 1’ | –40 | ||||
| –30 | 2’ | ||||
| 3’ | |||||
| –50 | 4’ | –60 | |||
| 5’ |
4.4.2. В табл. 4.11 приведен температурный коэффициент химической реакции для вашего варианта. При температуре 15 оС реакция заканчивается за τ мин. Определите время протекания реакции при температуре 35 оС.
Т а б л и ц а 4.11
| Вариант | γ | τ | Вариант | γ | τ |
| 6’ | 2,5 | ||||
| 2,5 | 12,5 | 7’ | |||
| 8’ | |||||
| 9’ | |||||
| 10’ |
4.4.3. На сколько градусов надо повысить температуру, чтобы скорость реакции для вашего варианта возросла в n раз при данном значении γ (табл. 4.12)?
Т а б л и ц а 4.12
| Вариант | n | γ | Вариант | n | γ |
| 11’ | 2,5 | ||||
| 12’ | |||||
| 2,5 | 13’ | ||||
| 14’ | |||||
| 15’ |
4.5. Напишите выражение и вычислите константу равновесия обратимой реакции, исходные и равновесные концентрации компонентов в системах (величины, которые нужно вычислить, обозначены через Х). Определите, в какую сторону сместится равновесие обратимой реакции при повышении температуры; как изменится скорость прямой и обратной реакций, если объем газовой смеси изменить в n раз (табл. 4.13).
Т а б л и ц а 4.13
| Вариант | Уравнение реакции | Кс | Равновес-ные концентра-ции, моль/л | Исходные концентра- ции, моль/л | ΔН 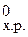 , кДж/моль , кДж/моль | n | |||||||||||
| 2SO2 + O2 ↔ ↔ 2SO3 | X | [SO2]=0,04; [O2]= 0,06; [SO3] = 0,02 | [SO2] = X1; [O2] = X2 | –196,6 | увеличить в 3 раза | ||||||||||||
| N2 + 3H2 ↔ ↔ 2NH3 | X | [N2] = 0,03; [H2] = 0,1; [NH3] = 0,4 | [N2] = X1; [H2] = X2 | –92,5 | уменьшить в 3 раза | ||||||||||||
| 2CO + O2 ↔ ↔ 2CO2 | X | [CO]=4[O2]; [CO2] = 2 | [CO] = X1; [O2] = X2 | –566,0 | увеличить в 2 раза | ||||||||||||
| CO + Cl2 ↔ ↔ COCl2 | 39,4 | [CO] = 0,2; [COCl2]=0,8 | [Cl2] = X | –112,5 | увеличить в 4 раза | ||||||||||||
| Продолжение табл. 4.13 | |||||||||||||||||
| CO+H2O (г) ↔ ↔ CO2 + H2 | [CO] = X1; [CO2] = X2; [H2O] = X3; [H2] = X4 | [CO]= 0,01; [H2O]=0,03 | –41,2 | уменьшить в 3 раза | |||||||||||||
| 2NO2 ↔ N2O4 | 7,15 | [NO2] = X | [NO2] = 3 | –58,0 | увеличить в 4 раза | ||||||||||||
| H2 + I2 (г) ↔ ↔ 2HI | X | [H2] = 0,1; [I2] = 0,2; [HI] = 0,6 | [H2] = X1; [I2] = X2 | 51,9 | уменьшить в 2 раза | ||||||||||||
| 4HCl + O2 ↔ ↔ 2H2O + 2Cl2 | X | [H2O]= =[Cl2]=0,14; [HCl] = 0,2; [O2] = 0,32 | [HCl] = X1; [O2] = X2 | –114,5 | увеличить в 2 раза | ||||||||||||
| Н2S + 4O2 ↔ ↔ SO3 + H2O | X | [H2S]= 0,72; [O2] = 1,12; [SO3]=0,84 | [H2S] = X1; [O2] = X2 | 163,1 | увеличить в 3 раза | ||||||||||||
| 2NO + O2 ↔ ↔ 2NO2 | X | [NO]=0,02; [O2]=0,3; [NO2]=0,06 | [NO] = X1; [O2] = X2 | –113,0 | уменьшить в 2 раза | ||||||||||||
| CO + Cl2 ↔ ↔ COCl2 | X | [COCl2]= =0,45 | [CO]=[Cl2]= =2 | –112,5 | уменьшить в 3 раза | ||||||||||||
| H2 + CO2 ↔ ↔ CO + H2O (г) | [H2O] = X | [H2]=[CO2]==2 | 41,2 | увеличить в 4 раза | |||||||||||||
| PCl5 (г) ↔ ↔PCl3 (г) + Cl2 | 0,041 | [Cl2]=0,1 | [PCl5]=X | 399,0 | уменьшить в 4 раза | ||||||||||||
| C(к)+H2O(г) ↔ ↔ CO + H2 | X | [H2]=0,2 | [H2O](г)=1 | 131,0 | увеличить в 2 раза | ||||||||||||
| N2O4↔ 2NO2 | X | [NO2]=0,8 | [N2O4]=X | 58,0 | увеличить в 4 раза | ||||||||||||
| Кр | |||||||||||||||||
| 1’ | SO3 + CO ↔ ↔ SO2 + CO2 | 1,89 | [SO3]=X [CO]=X2 [SO2]=X3 [CO2]=X4 | [SO3]=[CO]= = 0,95 | ΔH>0 | уменьшить в 2 раза | |||||||||||
| 2’ | 2HI ↔ H2 + I2 | 0,25 | [HI]=X1 [I2]=X2 | [HI] = 2,0 | –51,9 | увеличить в 3 раза | |||||||||||
| 3’ | SO2 + NO2 ↔ ↔ SO3 + NO | X | [SO2]=0,6 [NO2]=0,2 | [SO2]=X1 [SO3]=0 [NO2]=X2 | ΔH>0 | уменьшить в 4 раза | |||||||||||
| Окончание табл. 4.13 | |||||||||||||||||
| Кр | |||||||||||||||||
| 4’ | SO2 + Cl2 ↔ ↔ SO2Cl2 | X | [SO2Cl2]=1,5 | [SO2]=5,0 [Cl2]=4,0 | ΔH>0 | увеличить в 2 раза | |||||||||||
| 5’ | 2NO + O2↔ ↔ 2NO2 | 2,2 | [NO]=0,02 [NO2]=0,03 | [O2]=X | –113,0 | увеличить в 3 раза | |||||||||||
| 6’ | CH2O 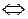 H2+CO H2+CO | X | [H2]=0,2 | [CH2O]=1,0 | ΔH>0 | уменьшить в 2 раза | |||||||||||
| 7’ | H2+I2↔ 2HI | [HI]=X | [H2]=2,0 [I2]=1,0 | 51,9 | увеличить в 2 раза | ||||||||||||
| 8’ | 3H2 + N2 ↔ ↔ 2NH3 | X | [NH3]=1,6 | [H2]=2,0 [N2]=1,0 [NH3]=0,4 | –91,5 | увеличить в 2 раза | |||||||||||
| 9’ | CO2 + H2 ↔ ↔ CO + H2O | 0,84 | [CO2]=X1 [H2]=X2 [CO]=X3 [H2O]=X4 | [CO2]=1,0 [H2]=1,5 | 41,2 | уменьшить в 3 раза | |||||||||||
| 10’ | 2NO2 ↔ 2NO + + O2 | X | [NO2]=0,006 [NO]=0,024 | [NO2]=X | 113,0 | уменьшить в 2 раза | |||||||||||
| 11’ | CO + H2O ↔ ↔ CO2 + H2 | 0,04 | [B]=0,05 [C]=0,02 | [A]=X1 [B]=X2 | –41,2 | увеличить в 3 раза | |||||||||||
| 12’ | CO2 + 2H2 ↔ ↔ CH3OH (г) | [CO2]=X1 [H2]=X2 [CH3OH]=X3 | [CO2]= =[H2]=0,02 | –161,3 | уменьшить в 3 раза | ||||||||||||
| 13’ | 2N2O ↔ 2N2 + + O2 | 0,65 | [N2O]=X1 [N2]=X2 [O2]=X3 | [N2O]=0,81 | –161,3 | увеличить в 4 раза | |||||||||||
| 14’ | 2H2S + 3O2 ↔ ↔ 2H2O + 2SO2 | 1,0 | [H2S]=X1 [O2]=X2 [H2O]=X3 [SO2]=X4 | [H2S]=1,0 [O2]=3,0 | –561,1 | уменьшить в 2 раза | |||||||||||
| 15’ | N2 + 2O2 ↔ ↔ 2NO2 | X | [NO2]=0,2 | [N2]=0,5 [O2]=0,8 | 67,5 | увеличить в 3 раза | |||||||||||
4.6. При нормальных условиях константа скорости реакции рав-на 1,18 моль/(л·мин), а при стандартных условиях – 6,56 моль/(л·мин). Определите температурный коэффициент скорости реакции.
4.7. Константа скорости реакции разложения N2O5 при 50 оС равна 6,2·10-4. Вычислите константу скорости этой реакции при 90 оС, исходя из того, что Еа равна 102 кДж/моль.
4.8. Средняя скорость реакции А (г) + В (г) = С (г) равна 0,004 моль/(л·с). Какова будет концентрация вещества А и В через 20 с, если их начальная концентрация была соответственно 2 и 3 моль/л?
4.9. В 10 л содержится 4 моль вещества А и 5 моль вещества В. Какова будет концентрация этих веществ через 4 с, если средняя скорость реакции А (г) + В (г) = С (г) равна 0,05 моль/(л·с)?
4.10. По какому веществу и во сколько раз скорость реакции А + 2В = С будет меньше, если концентрация вещества [A] уменьшилась на 0,05 моль/л?
4.11. По какому веществу и во сколько раз скорость реакции 2А + 3В = С будет меньше, если концентрация вещества [A] уменьшилась на 0,06 моль/л? Как при этом изменилась концентрация вещества [B]?
4.12. Во сколько раз необходимо повысить давление в газовой химической системе 2А + В = С, чтобы скорость образования вещества С возросла в 64 раза?
4.13. Средняя скорость гомогенной реакции составляет 10-3 моль/(л·с). С повышением температуры на каждые 10о она увеличивается в 2 раза. Какова будет концентрация продукта реакции после 10 с протекания реакции при условии, что температура повышена на 70 оС?
4.14. Реакция между веществами А и В выражается уравнением
А + 2В → С.
Начальные концентрации А и В соответственно равны 0,3 и 0,5 моль/л. Константа скорости k равна 0,4 л2/(моль2·с), реакция третьего порядка, тримолекулярная. Вычислите скорость химической реакции в начальный момент и в тот момент, когда концентрация вещества А уменьшится на 0,1 моль/л.
4.15. В гетерогенной системе
Si (к) + 2Н2О (г) ↔ SiO2 (к) + 2Н2 (г)
установилось равновесие с Кс = 0,1. Определите равновесные концентрации Н2О и Н2, если в начале реакции в реакторе объемом 20 л находилось 18 г паров воды.
4.16. Температурный коэффициент реакции равен 3,5. Константа скорости этой же реакции при 15 оС равна 0,2 с-1. Какова будет константа скорости реакции при 40 оС?
4.17. Как увеличить выход продуктов реакций
а) 2СО (г) ↔ СО2 (г) + С (к), ΔН 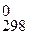 = –172,5 кДж/моль
= –172,5 кДж/моль
б) Н2 (г) + I2 (г) ↔ 2HI (г), ΔН 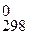 = 51,9 кДж/моль
= 51,9 кДж/моль
за счет изменения концентраций реагентов, давления, температуры?
4.18. Рассчитайте энергию активации реакции, если константы скорости этой реакции при 25 и 45 оС соответственно равны 3,43·10-5 и 4,73·10-4 моль/(л·с).
4.19. Рассчитайте энергию активации реакции 2HI (г) → Н2 (г) +
+ I2 (г), если при 302 оС константа скорости этой реакции равна 1,18·10-5 моль/(л·с), а при 374 оС – 8,94·10-5 л/(моль·с).
4.20. Во сколько раз следует увеличить давление в системе
Н2 (г) + I2 (г) = 2HI (г),
чтобы скорость образования HI возросла в 100 раз?
4.21. При повышении температуры на 30 оС скорость хими-ческой реакции увеличилась в 64 раза. Вычислите, во сколько раз увеличится скорость этой реакции при повышении температуры на каждые 10 о.
4.22. Рассчитайте температурный коэффициент реакции, если при нагревании системы от 40 до 80 оС скорость возросла в 64 раза.
4.23. Начальные концентрации веществ, участвующих в реакции
2NO (г) + O2 (г) = 2NO2 (г),
равны: [NO] = 0,50 моль/л; [O2] = 0,30 моль/л. Чему равна средняя скорость реакции, если через 15 с прореагировало 90 % NO?
4.24. Как изменится скорость реакции 2NO (г) + O2 (г)=2NO2 (г), кинетическое уравнение которой: v = k[NO]2[O2], при увеличении общего давления в 3 раза?
4.25. Определите энергию активации Еа реакции, для которой при повышении температуры от 22 до 32 оС скорость удваивается.
4.26. Вычислите энергию активации реакции, для которой константа скорости при 35 оС в два раза больше, чем при 25 оС.
4.27. Разложение вещества А происходит по двум параллельным стадиям:
1) А → В и 2) А → С.
Какова разница в энергиях активации реакций этих стадий, если при 20 оС k1/k2 = 0,1. Какая из реакций имеет более высокую энергию активации?
4.28. В сосуде объемом 10 л находится 12,8 г йодоводорода. После нагревания до некоторой температуры по реакции 2HI (г) = = H2 (г) + I2 (г) образовалось 5,12 г йода. Рассчитайте константу равновесия Кс.
4.29. В реакции, протекающей по уравнению 2HCl = H2 + Cl2, исходное давление рHCl = 1,3·105 Па. К моменту достижения равновесия парциальное давление водорода достигло 0,17·105 Па. Определите константу равновесия Кр.
4.30. Рассчитайте константу равновесия Кр для реакции
2SO2 (г) + O2 (г) = 2SO3 (г)
при Т1 = 1000 К и Т2 = 1100 К.
4.31. При постоянной температуре в гомогенной системе А + + В = 2D установилось равновесие с равновесными концентрациями [A] = 0,8 моль/л, [B] = 0,6 моль/л и [D] = 1,2 моль/л. Определите новые равновесные концентрации, если в систему дополнительно введено 0,6 моль/л вещества В.
4.32. Рассчитайте константу равновесия химической реакции при 1000 К, если стандартная энергия Гиббса при этой температуре равна –392 кДж/моль.
4.33. Стандартное изменение энергии Гиббса для реакции А+В 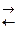 АВ при 298 К равно 8 кДж/моль. Начальные концентрации [A]0 = [B]0 = 1 моль/л. Найдите константу равновесия реакции.
АВ при 298 К равно 8 кДж/моль. Начальные концентрации [A]0 = [B]0 = 1 моль/л. Найдите константу равновесия реакции.
4.34. Вычислите температурный коэффициент скорости реак-ции, если константа скорости ее при 100 оС составляет 6.10-4, а при 150 оС – 7,2.10-2.
