Работа № 5. ОПРЕДЕЛЕНИЕ ПАРЦИАЛЬНО-МОЛЯРНЫХ ОБЪЕМОВ КОМПОНЕНТОВ БИНАРНОГО РАСТВОРА
В данной работе изучается зависимость парциально-молярных объемов компонентов раствора "вода - этиловый спирт" от химического состава.
Подготовка к работе требует усвоения следующих разделов теоретического курса: понятие парциально-молярного свойства компонента раствора, уравнение Гиббса-Дюгема и следствия из него, идеальные растворы и причины отклонений от свойств идеальных растворов в реальных системах.
Теоретические сведения
Любое экстенсивное свойство раствора при фиксированных температуре и давлении зависит от числа молей компонентов, составляющих раствор. Так, для бинарного раствора экстенсивное свойство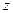 
является функцией внешних параметров 
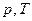и чисел молей 
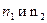, то есть
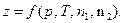 | (51) |
Полный дифференциал свойства может быть выражен через частные производные и приращения независимых переменных. Поэтому при постоянных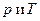 
:
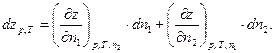 | (52) |
Частную производную экстенсивного свойства раствора 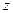по числу молей данного компонента при постоянных 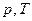и числах молей остальных компонентов называют парциально-молярным свойством компонента. То есть парциально-молярное свойство 
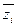это приращение общего молярного свойства 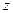раствора, получающегося в результате добавления в раствор заданного состава бесконечно малого количества растворенного вещества при p, T = const и постоянном составе раствора, пересчитанное на 1 моль растворенного вещества:
 | (53) |
Представим уравнение (52) в виде
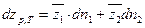 | (54) |
или для многокомпонентного раствора:
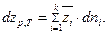 | (55) |
Парциально-молярные свойства компонентов раствора зависят от 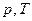и химического состава, причем их изменения взаимно связаны. Эта связь при 
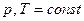устанавливается уравнением Гиббса-Дюгема
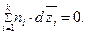 | (56) |
В случае бинарного раствора уравнение (55) может быть записано в форме
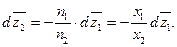 | (57) |
Из уравнения (57) следует, что приращения свойств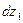 
и 
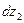противоположны по знаку, то есть, если с увеличением концентрации одного из компонентов его парциально-молярное свойство растет, то для другого оно обязательно уменьшается. Анализ уравнения (57) показывает также, что интенсивнее с составом раствора меняется свойство компонента, концентрация которого в растворе меньше.
В данной лабораторной работе исследуются парциально-молярные свойства раствора на примере определения парциально-молярных объемов компонентов бинарного раствора, то есть общее молярное свойство z – это молярный объем Vm. И применяя приведенные выше выражения для системы «вода-спирт» получим:
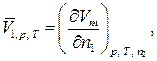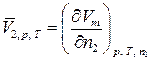  | (58) |
Уравнение Гиббса-Дюгема для парциально-молярных объемов компонентов бинарного раствора:
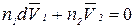 | (59) |
Поскольку любое свойство раствора складывается аддитивно из парциально-молярных свойств компонентов, то мольный объем бинарного раствора
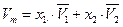 | (60) |
В этом выражении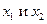 
- мольные доли компонентов, равные отношению числа молей данного компонента к общему числу молей всех компонентов раствора.
Часто для определения величин 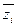компонентов бинарного раствора используют графический метод, требующий знания зависимости мольного свойства 
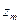от мольной доли одного из компонентов.
Допустим, эта зависимость для молярного объема известна и представлена на рис. 10.
Докажем, что отрезок Оа, отсекаемый касательной AM, проведенной к кривой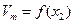 
в точке М, численно равен парциально-молярному объему первого компонента в растворе состава 
.
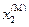Из рисунка следует, что для любой выбранной мольной доли второго компонента (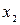 
), в том числе и для 
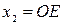, справедливо равенство:
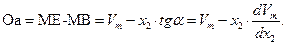 | (61) |
В бинарном растворе
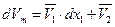  , | (62) |
a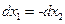 
, т.к. 
.
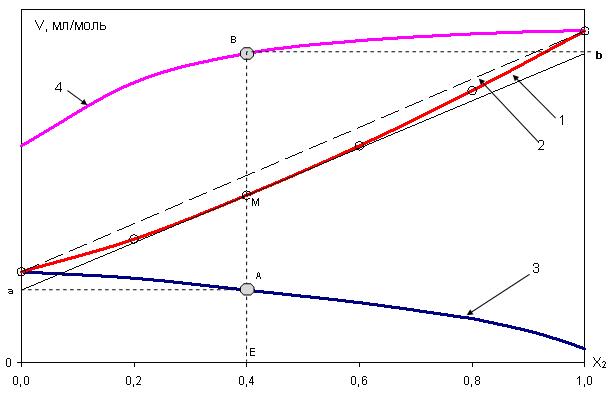
Рис. 10 – к определению парциально-молярных объемов раствора
Учитывая это обстоятельство и соотношение (57), запишем равенство (58) в виде:
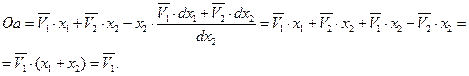 | (63) |
Таким образом, отрезок Оа, отсекаемый касательной на оси ординат при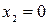 
, равен парциально-молярному объему первого компонента. Аналогично отрезок, отсекаемый этой касательной аb на оси ординат справа, то есть при 
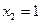, соответствует величине 
.
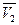Кривая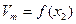 
на рис. 10 проходит ниже аддитивной прямой (пунктир), характерной для идеальных растворов, где
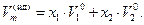 | (64) |
Причиной отклонения молярного объема реального раствора от такового для идеального является различие в энергиях связи между различными частицами раствора. Если энергия связи разноименных частиц (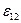 
) больше средней энергии связи одноименных ( 
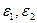), то есть
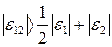 , | (65) |
и образование раствора сопровождается его уплотнением.
Подобная зависимость характерна для растворов с отрицательными отклонениями от идеального раствора. При значительных различиях в энергиях связи парциально-молярный объём компонента может оказаться отрицательным, что говорит об уменьшении общего объема раствора при добавлении к нему данного компонента.
Порядок выполнения работы
Молярный объем раствора можно найти из очевидного соотношения
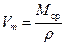 =  | (66) |
в котором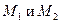 
– молярные массы компонентов раствора, а 
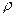– плотность раствора.
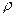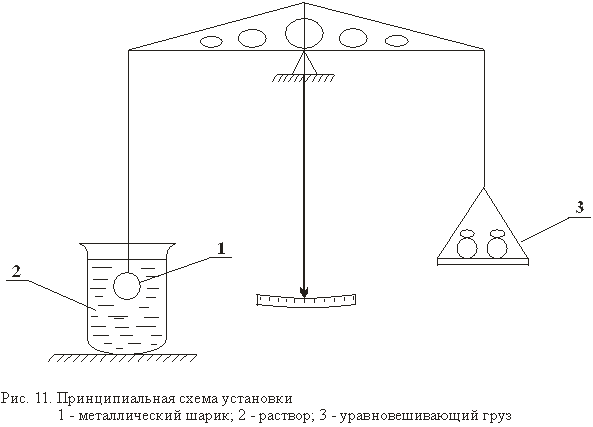
Плотность раствора , необходимую для расчета молярного объема 
, можно определить методом взвешивания металлического шарика последовательно на воздухе, в чистой воде и в данном водном растворе. Для этой цели в работе используются аналитические весы, к одному из коромысел которых подвешен металлический грузик (I) объемом около 1см3 (см. рис. 11).
При взвешивании, шарика объемом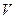 
и плотностью 
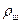, находящегося в какой-либо среде (воздух, вода, раствор) плотностью 
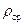, следует учесть выталкивающую силу Архимеда 
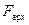, поэтому измеряемый вес в среде ( 
)
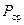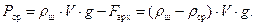 | (67) |
Записывая уравнение (64) для трех сред (воздух, вода и раствор), получим систему трех уравнений с тремя неизвестными величинами (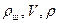 
). Её решение дает следующую расчетную формулу для плотности раствора:
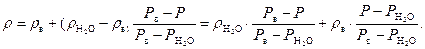 | (68) |
Поскольку плотность воздуха мала и составляет при нормальных условиях 0,0013 г/см3, а множитель, стоящий после нее в уравнении (65), значительно меньше единицы, то для практических расчетов целесообразно воспользоваться формулой
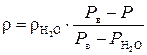 | (69) |
Взвешивание шарика в растворе проводится три раза по схеме: колба №1, №2, №3, ... ; №1, №2, №3 ... ; №1, №2, №3 ... ; Результаты взвешивания вносят в табл. 6.
Таблица 6
Результаты взвешивания
| x2 P | 0,2 | 0,4 | 0,6 | 0,8 | |
| PI | |||||
| PII | |||||
| PIII | |||||
 |
По результатам трех взвешиваний по формуле (4) согласно пункту 2 на стр. 8 руководства «Термодинамика» следует найти случайную среднеквадратическую погрешность определения молярного объема ( 
), затем определить относительную погрешность измерения величин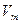 
. По этим данным оценить целесообразное число значащих цифр в результате и заполнить колонку 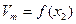табл. 7.
Таблица 7
Результаты определения величин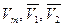 
| x2 V, м3/моль | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
| | ||||||
 | ||||||
 |
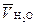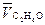Величину 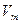чистого этилового спирта необходимо рассчитать по табличному значению плотности 
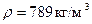( t = 20 °С). Затем, построив график зависимости мольного объема раствора от состава, определить графическим методом величины 
, 
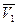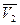и заполнить окончательно табл. 6. Возможен и вариант машинного расчета величин 
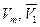и 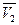по заранее составленной программе (по усмотрению преподавателя).
Вопросы для самоконтроля
1. Что называют парциально-молярной величиной 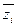любого свойства компонента в растворе; поясните физический смысл величины ?
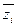2. Запишите уравнение Гиббса-Дюгема и поясните физический смысл входящих в него величин.
3. Каким методом в работе определяют парциально-мольный объем компонентов?
4. Выше или ниже аддитивной прямой, характерной для идеальных растворов, пойдет зависимость мольного объема раствора, если смешение чистых жидких компонентов I и 2 происходит с выделением большого количества тепла?
5. Зависимость объема раствора, содержащего 50 молей воды и n2 молей растворенного вещества, передается уравнением:
 |
Определите парциально-молярный объем растворенного вещества, мольный объем раствора и величину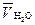 
, если раствор содержит один моль растворенного вещества.
6. При добавлении малых порций растворенного вещества к растворителю мольный объем раствора не изменяется. Чему равен парциально-молярный объем растворенного вещества, если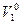 
=20 см3/моль, а 
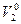=12 см3/моль?