Правила процесса восстановления на катоде и окисления на аноде

В общем случае из нескольких возможных полуреакций на катоде будет протекать та, электродный потенциал которой больше. Практически при электролизе водных растворов солей следует руководствоваться следующими правилами для определения протекающего на катоде процесса восстановления:

1) если металл, образующий соль, стоит в ряду напряжений до Al включительно, то восстанавливаются молекулы воды и выделяется водород;

2) если металл, образующий соль, стоит в ряду напряжений после Al, но до водорода, то восстанавливаются и катионы металла, и молекулы воды;

3) если металл, образующий соль, стоит в ряду напряжений после водорода, то восстанавливаются катионы металла.

Металлы в электрохимическом ряду напряжений располагаются в порядке возрастания стандартных электродных потенциалов полуреакций:

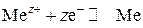
Ряд начинается с активных металлов (первым стоит Li) и заканчивается неактивными (благородными металлами, Pt, Au). Электрохимический ряд напряжений металлов для некоторых металлов представлен ниже:

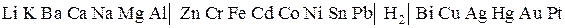
Катодные процессы в водных растворах солей

Li…………Al	Zn……………Pb	H	Bi………..Pt
2H2O + 2e– = H2 + 2OH–	Меn+ + ne– = Мео 2H2O + 2e– = H2 + 2OH–		Меn+ + ne– = Мео

При электролизе растворов кислот на катоде восстанавливаются катионы водорода до молекулярного водорода:

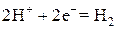
В общем случае из нескольких возможных полуреакций на аноде будет протекать та, электродный потенциал которой меньше. Процессы, протекающие на аноде, зависят от материала анода. Практически при электролизе водных растворов солей следует руководствоваться следующими правилами для определения протекающего на аноде процесса окисления:

1) если анод растворимый, то окисляется металл, из которого состоит анод, до катионов металла;

2) если анод нерастворимый, а анион бескислородный (Cl^–, Br^–, I^–, S^2–, кроме F^–), то окисляется анион до соответствующего простого вещества (Cl₂, Br₂, I₂, S);

3) если анод нерастворимый, а анион кислородсодержащий, то окисляются молекулы воды:

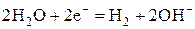
При электролизе растворов щелочей на аноде окисляются гидроксид-ионы до молекулярного кислорода:

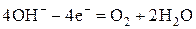
Анодные процессы в водных растворах

Нерастворимый анод	Растворимый анод
Кислотные остатки	ОН–
бескислородных кислот	кислородсодержащих кислот, F–
2Cl– – 2e– = Cl2 S2- – 2e– = S	2H2O - – 4e– = O2 + 4H+	4OH– – 4e– = O2 + 2H2O	Мео – ne– = Меn+

При составлении схемы электролиза следует записать уравнения полуреакций на катоде, на аноде и суммарное уравнение электролиза. В случае, если на катоде протекают оба процесса восстановления воды и катионов металла, суммарное уравнение электролиза на записывают.

Пример 1. Составьте схему электролиза расплава хлорида калия на графитовых электродах.

Решение. Графитовые электроды нерастворимы и не участвуют в электродных процессах. В расплаве хлорид калия распадается на ионы:

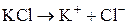
При электролизе расплава соли на катоде восстанавливаются катионы металла до свободного металла, а на аноде окисляются анионы бескислородных кислот. Составляем схему электролиза:

К-: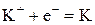
А+: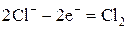

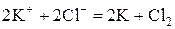Суммарное уравнение электролиза в молекулярной форме имеет вид:

.

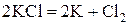Пример 2. Составьте схему электролиза водного раствора: а) хлорида натрия на графитовых электродах; б) сульфата цинка на нерастворимых электродах; в) сульфата меди на медных электродах.

Решение. При составлении схемы электролиза водных растворов солей будем руководствоваться приведенными выше правилами восстановления на катоде и окисления на аноде.

а) Хлорид натрия в растворе диссоциирует на ионы:

.

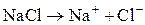На катоде будут восстанавливаться молекулы воды, так как Na стоит в ряду напряжений до Al. На нерастворимом аноде будет окисляться бескислородный анион Cl^–:

К-: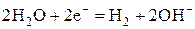
А+: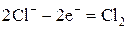

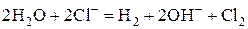В молекулярном виде:

.

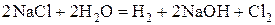б) Сульфат цинка диссоциирует на ионы в растворе:

.

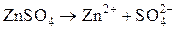На катоде будут восстанавливаться молекулы воды и катионы цинка, поскольку Zn стоит в ряду напряжений между Al и H₂. На нерастворимом аноде будут окисляться молекулы воды, так как анион 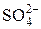кислородсодержащий:

К-: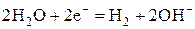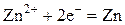
А+: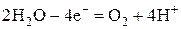

Поскольку на катоде идет два процесса, суммарное уравнение электролиза не составляется.

в) Сульфат меди диссоциирует в растворе на ионы:

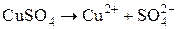
На катоде будут восстанавливаться катионы меди, так как Cu стоит в ряду напряжений после H₂. На растворимом медном аноде будет идти окисление металла анода, т. е. меди до катионов меди:

К-: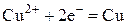
А+: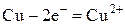

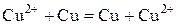В данном случае при электролизе в системе никаких новых продуктов не образуется. Процесс электролиза сводится к растворению меди на аноде и осаждению ее на катоде. Этот процесс называется электролитическим рафинированием и используется для получения чистых металлов.

Минимальное напряжение, которое необходимо приложить от внешнего источника тока для протекания процесса электролиза называется напряжением разложения. Его можно рассчитать как разность электродных потенциалов с учетом перенапряжений:

,

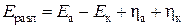где E_разл – напряжение разложения, В; E_а, E_к – электродные потенциалы полуреакций, протекающих на аноде и катоде соответственно, В; h_а, h_к – перенапряжения анодной и катодной полуреакций соответственно, В.

Перенапряжение – разность потенциала электрода под током и в отсутствие тока. Оно зависит от природы веществ, участвующих в полуреакции, материала электрода, состава раствора или расплава, силы тока, температуры и многих других факторов.

Самые большие значения перенапряжения наблюдаются в случае образования на электродах водорода и кислорода. При этом величина перенапряжения в наибольшей степени зависит от материала электрода. Приближенные значения перенапряжений выделения водорода и кислорода в зависимости от материала электрода приведены в справочниках. При этом выделение водорода в нейтральной и щелочной среде идет в соответствии с полуреакцией

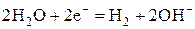
а выделение кислорода в нейтральной и кислой среде – согласно полуреакции

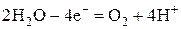
Законы Фарадея

Количественные закономерности электролиза определяются законами Фарадея, которым можно дать следующую общую формулировку: массы (объемы для газов) исходных веществ и продуктов окис-лительно-восстановительной реакции, протекающей при электролизе, прямо пропорциональны количеству электричества, пропущенного через раствор или расплав электролита, и молярным массам эквивалентов (молярным объемам эквивалентов для газов) соответствующих веществ. Закон Фарадея выражается следующим уравнением:

,

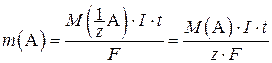где m(A) – масса вещества А, г; 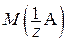– молярная масса эквивалента вещества А, г/моль; I – сила тока, А; t – время электролиза, с; F – постоянная Фарадея, равная 96 484 Кл/моль; M(A) – молярная масса вещества А, г/моль; z – число эквивалентности.

Число эквивалентности z в окислительно-восстановительной реакции определяется числом электронов, эквивалентных одной молекуле вещества. Произведение силы тока на время электролиза представляет собой количество пропущенного электричества.

В случае газообразного вещества A закон Фарадея можно также выразить следующим уравнением:

,

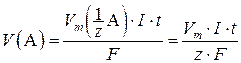где V(A) – объем вещества А, л; 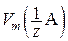– молярный объем эквивалента вещества А, л/моль; V_m – молярный объем газа, равный 22,4 л/моль при н. у.

Пример. Определите объем (н. у.) выделившегося на нерастворимом аноде кислорода при электролизе раствора гидроксида натрия, если через раствор пропускали ток силой 300 мА в течение 1 ч.

Решение. Составляем схему электролиза (чтобы найти z):

.

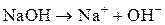На катоде восстанавливается вода (Na стоит до Al), на аноде окисляются гидроксид-ионы:

К-: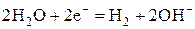
А+: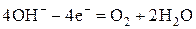

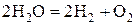Электролиз сводится к разложению воды.

Объем выделившегося кислорода находим по формуле.

Переводим время из часов в секунды: t = 1 × 60 × 60 = 3600 c.

Силу тока представляем в амперах: I = 0,3 А.

Число эквивалентности z можно определить по уравнению окисления воды на аноде (см. выше): на получение одной молекулы кислорода приходится 4 электрона, значит, z = 4.

Вычисляем объем выделившегося кислорода:

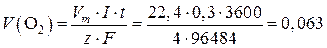л.

СТРОЕНИЕ АТОМА

Атомы и составляющие их частицы относятся к микроскопическим телам. Свойства таких частиц определяются их движением и взаимодействием. Явления, связанные с поведением частиц микромира, удается понять и описать только на основании законов и представлений квантовой механики.

Квантовая механика представляет собой теорию, устанавливающую способ описания и законы движения микрочастиц в заданных внешних полях. Она позволяет описать структуру атомов, расшифровать их спектры, установить природу химической связи. В отличие от представлений классической физики все частицы в квантовой механике рассматриваются как носители корпускулярных и волновых свойств, которые не исключают, а дополняют друг друга. Представления о дуализме (двойственной природе) материи потребовали нового подхода к описанию состояния физических систем и их изменения во времени. Из квантовой механики вытекает, что не все физические величины могут одновременно иметь точные значения.

Отличительная черта квантовой теории – дискретность. Дискретность в переводе с латинского языка означает «разделенный, прерывистый, изменение, происходящее скачками». В начале прошлого века немецкий физик М. Планк в процессе изучения распределения теплового излучения, испускаемого нагретыми телами, установил, что энергия излучается не непрерывно, а квантами, равными величинам h :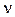

Е = h 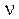, (1)

где Е – энергия кванта; 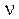– частота колебания; h – квант действия, позже названный постоянной Планка.

Постулат Планка положен в основу квантовой механики. Выражение (1) стало количественной основой гипотезы, согласно которой атомы принимают и излучают энергию квантами, мельчайшими, далее неделимыми порциями. Постоянная Планка h разграничивает области явлений, которые можно описывать с применением законов классической физики, в этих случаях ее можно считать равной нулю, и области, для правильного истолкования которых необходима квантовая теория.

Ко времени появления квантовой механики уже было известно, что электромагнитное излучение способно обнаруживать как волновые, так и корпускулярные свойства. Эти представления Луи де Бройль перенес на электроны. Из совместного решения уравнений (1) Планка и уравнения (2) Эйнштейна

Е = mc² (2)

следует, что h 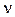= mс².

Выразим 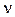через с и 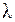, для фотона получим 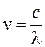. Особенностью фотонов является то, что они не имеют массы покоя и существуют лишь при движении со скоростью света.

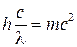или .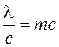

Для материальной точки с массой m и скоростью движения 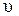уравнение принимает вид, предложенный де Бройлем:

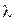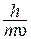= , (3)

где 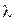- длина волны электрона; h - постоянная Планка; m - масса электрона; 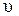- его скорость; с - скорость света.

Электроны движутся со скоростями существенно меньшими, чем скорость света. Скорость света в пустоте равна 2,997 925 · 10⁸ м/с, скорость движения электрона на первой, самой близкой к ядру орбите равна 2 185 000 м/с.

Из уравнения де Бройля следует, что движение микрочастиц связано с распространением волн. Уравнение (3) связывает количество движения m 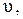характеристику вещественной формы существования материи с характеристикой материального поля, длиной волны 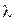через фундаментальную константу природы h.

Следующим шагом на пути создания волновой механики была идея, сформулированная В. Гейзенбергом. Эта идея объясняла двойственную природу электрона, она появилась почти одновременно с идеей де Бройля.

Принцип неопределенности Гейзенберга: для тел атомного масштаба нельзя указать одновременно их точное положение в пространстве и направление движения.

Можно указать только вероятность нахождения электрона в определенном положении в любой момент времени. Математическое выражение принципа неопределенности:

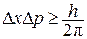, (4)

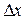где и 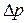обозначают неопределенности в измерении координаты и импульса частицы.

Из этого принципа следует, что траекторию частицы атомного масштаба нельзя рассматривать с математической точностью. Существует полоса неопределенности, в которой частица может двигаться по всей области возможных положений.

Представления о волновой природе электронов получили экспериментальное подтверждение. Было установлено, что пучок электронов может давать дифракционный эффект, характерный только для волн. Длины волн, полученные экспериментально, совпали с рассчитанными по уравнению де Бройля.

Квантовая механика описывает атом как систему стоячих волн вокруг ядра. Систему стоячих волн можно представить как струны, концы которых закреплены, и они могут колебаться с определенными частотами. На определенном очень малом расстоянии от ядра атома амплитуды этих волн становятся незначительными, как бы ограничивая тем самым размер атома.

В качестве модели для описания поведения электрона в атоме В. Шредингер предложил использовать волновое уравнение классической механики:

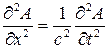, (5)

где А - амплитуда волны; с - скорость перемещения волны; t - время перемещения волны.

Для описания модели атома, движение которого подобно стоячей волне, Шредингер предложил уравнение, не содержащее скорости и времени:

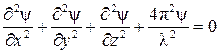, (6)

где 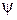- трехмерный аналог величины А в уравнении (5), а x, y, z - координаты трехмерного пространства.

Если в уравнение (5) подставить значение длины волны (3), то оно будет иметь вид

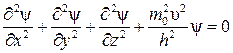. (7)

Известно, что полная энергия системы Е равна сумме потенциальной U икинетической m₀ 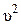/2 энергий:

Е = U + m₀ 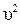/2. (8)

Выразив из уравнения (8) 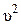и подставив его в уравнение (7), получим

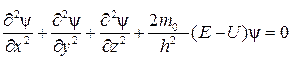. (9)

Уравнение (9) позволяет определить значение волновой функции 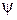. Квадрат ее модуля | 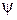²| определяет вероятность данного состояния и, следовательно, вероятности для значений физических величин, характеризующих данное состояние.

Волновая функция 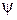- это характеристика электрона, она имеет определенное значение в любой точке пространства и формально является трехмерным аналогом амплитуды плоской волны. Квадрат волновой функции 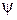² пропорционален вероятности нахождения частицы (электрона) в данной области пространства с координатами x, y, z. Если электрон рассматривать как размытое распределение отрицательного заряда в пространстве, то 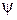² - вероятность нахождения электрона в данной единице объема пространства. Точное положение электрона в пространстве в любой момент времени определить нельзя, но с помощью квадрата волновой функции можно указать вероятность его нахождения в определенном положении в любой момент времени. Решение уравнения Шредингера позволяет найти вид волновой функции и энергию электрона.

В приложении к атомам волновая механика дает те же результаты, что и боровская модель для уровней энергии электрона в атоме водорода, но в то же время с ее помощью можно правильно описать свойства более сложных атомов, чем атом водорода.

Решения волнового уравнения Шредингера могут быть получены только при определенных условиях. На орбите, по которой движется электрон, должно укладываться целое число длин волн. Число раз, которое длина волны укладывается на орбите, соответствует квантовому числу электрона n.

Область пространства, в которой вероятность обнаружения электрона составляет 95%, называется орбиталью. Орбиталь – не одно и то же, что орбита в теории Бора, в которой под орбитой понимают путь электрона вокруг ядра. С позиций квантовой механики можно говорить только о вероятности пребывания электрона в данной фиксированной точке пространства, локализованной траектории движения у электрона нет.

Для одноэлектронной системы электрон как бы размазан вокруг ядра по сфере, удаленной от ядра на некотором расстоянии, образуя электронное облако неравномерной плотности. Максимальная электронная плотность отвечает наибольшей вероятности нахождения электрона и определяется квадратом волновой функции.

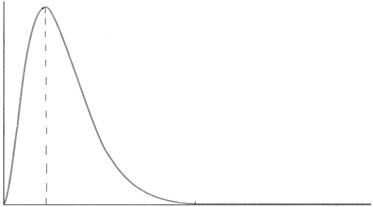
График функции радиального распределения электронной плотности для самой стабильной орбитали атома водорода представлен на рис. 1. 4pr²R(r)²

0 r₀ r, нм

Функция радиального распределения электронной плотности
для 1s-атомной орбитали

На графике показано, как меняется доля электронной плотности, находящаяся в каждом тонком сферическом слое, по мере удаления от ядра. На ядре функция 4 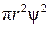равна нулю, а затем проходит через максимум. Положение максимума совпадает с первым радиусом Бора r₀ = 0,0529 нм.

Решение уравнения Шредингера всегда содержит некоторые безразмерные параметры, представляющие собой квантовые числа n, l, m_l. Собственные функции 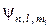называют орбиталями, для их описания используют набор квантовых чисел. Орбитали могут быть представлены трехмерными ограничивающими их поверхностями, каждая имеет свою определенную форму.

Квантовые числа

Энергетическое состояние электрона в атоме характеризуется четырьмя квантовыми числами. С их помощью можно описать строение его электронной оболочки.

n - главное квантовое число. Оно может принимать целочисленные значения 1, 2, 3, ×××, 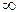. Главное квантовое число характеризует расстояние электрона от ядра или размер электронного облака, номер электронного уровня, общую энергию электрона на данном уровне. Его значение соответствует числу подуровней.

l - орбитальное (побочное) квантовое число. Оно определяет форму электронного облака, принимает значения 0, 1, 2, ×××, (n – 1). Число значений l определяет число возможных для данного электронного уровня подуровней. Электроны могут занимать орбитали четырех разных типов в зависимости от значения l, которые называют s-, p-, d- и f-орбиталями. Буквенные обозначения соотносятся с численными следующим образом:

0, 1, 2, 3

s p d f.

m_l - магнитное квантовое число. Оно связано с пространственной ориентацией движения электрона во внешнем магнитном поле, учитывает влияние на энергию электрона пересечения электроном магнитных полей в атоме. Если электрон вращается по орбитали, пересекающей линии магнитного поля в перпендикулярном направлении, магнитное взаимодействие полей атома и электрона оказывается максимальным. Если электрон вращается в плоскости распространения магнитных силовых линий, то вклад магнитного взаимодействия в общий запас энергии электрона минимален. Для данных n и l квантовое число m_l может иметь значения 0, ±1, ±2, ×××, ±l. Число значений m_l соответствует числу орбиталей в подуровне.

m_s – спиновое квантовое число. Оно характеризует спиновый момент количества движения, так как электрон обладает еще одним видом движения, движением вокруг собственной оси. Поскольку такое вращение может иметь только два направления (по часовой стрелке и против нее), спиновое квантовое число имеет только два значения: +1/2 и –1/2.

Возможные значения четырех квантовых чисел для всех электронов, которые могут располагаться на первых четырех энергетических уровнях, приведены в табл. 1. Каждый электрон имеет свой набор квантовых чисел.

Таблица 1