Кулоновские и сторонние силы. Электродвижущая сила

РАБОТА № 210

ИЗУЧЕНИЕ МЕТОДА КОМПЕНСАЦИИ И ПРИМЕНЕНИЕ ЕГО ДЛЯ ИЗМЕРЕНИЯ МАЛЫХ ЭЛЕКТРОДВИЖУЩИХ СИЛ

Теория

Кулоновские и сторонние силы. Электродвижущая сила.

Электроны и ионы в проводниках создают электростатическое поле, называемое полем кулоновских сил. Кулоновские силы взаи­модействия между зарядами всегда приводят к такому перераспределению свободных зарядов, при котором электрическое поде в проводнике исчезает, а потенциалы во всех точках выравниваются. Поэтому поле кулоновских сил не может вызвать стационарный процесс упорядоченно­го движения зарядов, т.е. не может являться причиной возникновения постоянного электрического тока.

Для поддержания постоянного тока в цепи на свободные заряды должны действовать, помимо кулоновских сил, так называемые с т о р о н н и е с и л ы.

Если кулоновские силы вызывают соединение разноименных зарядов, что ведет к выравниванию потенциалов, то сторонние силы вызывают разделение разноименных зарядов и поддерживают разность потенциалов на концах электрической цепи. Добавочное электрическое поле - поле сторонних сил в цепи - создается источниками тока (гальваническими элементами, аккумуляторами, электрическими генераторами). Перемещая электрические заряды, сторонние силы совершают работу за счет энер­гии, затрагиваемой в источнике тока. Так, например, в электромагнитном генераторе тока (динамо машине) работа сторонних сил соверша­ется за счет механической работы, затрачиваемой на вращение ротора генератора. В гальванических элементах эта работа совершается за счет энергии, которая выделяется при химических процессах растворе­ния электродов в электролите.

Величина, численно равная работе сторонних сил по перемещению единичного положительного заряда из точки I в точку 2 электрической цепи, называется электродвижущей силой источника тока ε , включенного на этом участке цепи, т.е.

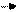
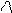
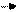
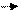
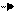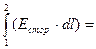
ε = /Е_стор./·|dl |·Cos(E_стор.,dl),

где E_стор - вектор напряженности поля сторонних сил.

Величина, численно равная работе кулоновских сил по перемещению единичного положительного заряда на участке цепи между точками I и 2, называется разностью потенциалов на этом участке цепи 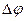, т.е

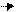
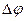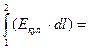
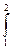= /Е_кул./·|dl|·Cos(E_кул.,dl),

где, Е_кул.- вектор напряженности поля кулоновских сил.

Под действием кулоновских сил положительный заряд перемешается от более высокого к более низкому потенциалу. Работа кулоновских сил при перемещении заряда по замкнутому контуру равна нулю, т.е. поле кулоновских сил является полем потенциальным.

Под действием сторонних сил положительный заряд перемешается от более низкого к более высокому потенциалу.

Поле сторонних сил не является полем потенциальным, т.е. рабо­та сторонних сил по перемещению заряда по замкнутому контуру не равна нулю. Следовательно, работа по перемещению заряда по замкнутой цепи совершается лишь сторонними силами, а на отдельных участках цепи как сторонними, так и кулоновскими силами.

Величина, численно равная сумме работ сторонних и кулоновских сил по перемещению единичного положительного заряда на данном участке цепи, называется напряжением, т.е.

U₁₂= ε +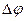

По закону Ома для участка цепи напряжение численно равно произведению силы тока J на сопротивление участка цепи R , т.е.

U₁₂= J R₁₂= ε +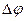

Для замкнутой цепи 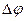= 0, а R₁₂=R=r - сопротивление всей цепи, где r - сопротивление внутреннего участка цепи (сопро­тивление источника тока), R- сопротивление внешнего участка цепи, т.е.

ε = J (R+r)= J R+Jr=U_внеш.+U_внутр.

- закон Ома для замкнутой цепи.

Присоединение вольтметра к полюсам источника тока (рис.1) соз­дает замкнутую цепь, для которой R = Rv - сопротивление вольтметра. Согласно закону Ома для замкнутой цепи:

U_внеш.=JR_v=ε-Jr, т.е. показание вольтметра (U_внеш.= JR_v) отличается от ЭДС источника тока на величину U_внутр.= J·r .

В тех случаях, когда сопротивление вольтметра велико R_v>>r (например, для лампового вольтметра), ток в цепи вольтметра мал и Jr 0, т.е. показание вольтметра можно считать за величину ЭДС источника тока. При точных измерениях ЭДС применяются специальные методы, например, метод компенсации.

§ 2. Описание метода компенсации. Принципиальная схема измере­ний ЭДС методом компенсации изображена на рис.2.

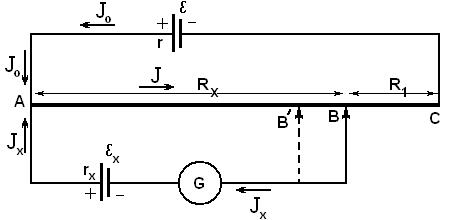
Рис.2

В схеме два элемента с электродвижущими силами ε и ε _х и внутренними сопротивлениями r и r_x присоединены к некоторому со­противлению R=R_x + R₁ (R_x и R₁ - соответственно сопро­тивления участков АВ и ВС) и гальванометру G с сопротивлением R_G.

Обозначим через J, J_o, J_x токи идущие в отдельных участ­ках схемы. Если ε _х < ε, то на сопротивлении R всегда можно найти такую точку В, что в ветви АGВ тока не окажется, и стрелка гальванометра G будет стоять на нуле. По второму закону Кирхгофа для контура АВGА можно написать

J_x (r_x + R_G ) + J R_x = ε_х

Когда ток через гальвонометр J_G =0, то

J R_x = ε_х . (1)

Полученное условие означает, что сила тока в цепи элемента ε_х лишь тогда равна нулю, когда напряжение на участке цепи АВ, параллельно которому присоединен этот элемент, равно его электродвижущей силе. В подобных случаях тшнято говорить о взаимной компенсации напряжения и ЭДС.

Введем в схему вместо элемента ε_х элемент ε_N и вновь до­бьемся отсутствия тока в цепи гальванометра и этого элемента при сопротивлении участка цепи АВ^/' равном некоторому значению R_N . Теперь выражение (1) можно записать в таком виде

J R_N = ε_N . (2)

Разделив соотношение (1) на (2), получим

ε_х = ε_N R_x / R_N . (3)

Если ЭДС ε_N известна, например, если это нормальный элемент (нормальный элемента- гальванический элемент, который при постояной температуре и давлении дает устойчивую ЭДС), то, зная R_x , R_N и ε_N можно найти из последнего равенства ЭДС ε_х. Таким образом, сравнение электродвижущих сил двух элементов практически сводится к сравнению двух сопротивлений.

Метод компенсации для измерения ЭДС обладает рядом существенных достоинств. Во-первых, сила тока через сравниваемые элементы в момент компенсации равна нулю. Поэтому отсутствует напряжение в элементе, и разность потенциалов на полюсах элемента равна измеряе­мой ЭДС. Кроме того, отсутствует также и падение напряжения на под­водящих проводах. Во-вторых, величина ЭДС вспомогательной батареи ε не входит в окончательный результат. Необходимо только, чтобы она оставалась постоянной в продолжении измерения, а также превыша­ла значения ЭДС сравниваемых элементов.