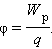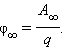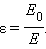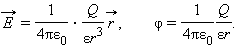Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника.
Поток вектора напряженности. Теорема Гаусса Электростатического поля и расчету поля бесконечной равномерно заряженной прямой нити.
Полное число силовых линий, проходящих через поверхность S называетсяпотоком вектора напряженностиФЕчерез эту поверхность.
В векторной форме можно записать 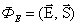 – скалярное произведение двух векторов, где вектор
– скалярное произведение двух векторов, где вектор 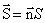 .
.
Следовательно, поток вектора напряженности E через площадку dS запишется в виде:
 |
где a – угол между векторами E и n, En - нормальная к поверхности dS составляющая вектора E.
Поток вектора E через произвольную поверхность S равен интегралу по этой поверхности
 |
Теорема Гаусса-Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
-
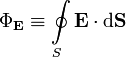 — поток вектора напряжённости электрического поля через замкнутую поверхность
— поток вектора напряжённости электрического поля через замкнутую поверхность 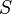 .
.
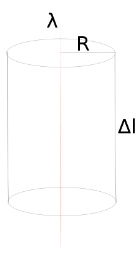
Расчёт напряжённости поля бесконечной нити
Рассмотрим поле, создаваемое бесконечной прямолинейной нитью с линейной плотностью заряда, равной 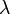 . Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии
. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии 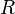 от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом
от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом 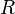 и высотой
и высотой 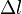 . Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицахСИ):
. Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицахСИ):
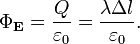
В силу симметрии
вектор напряжённости поля направлен перпендикулярно нити, прямо от нее (или прямо к ней).
модуль этого вектора в любой точке поверхности цилиндра одинаков.
Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом:
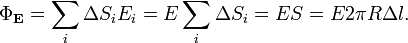
Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю (вследствие направления Eпо касательной к ним). Приравнивая два полученных выражения для 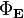 , имеем:
, имеем:
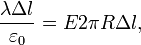
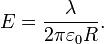
Работа перемещения заряда в электростатическом поле. Потенциал. Циркуляция вектора напряженности электростатического поля. Связь между напряженностью электростатического поля и потенциалом. Силовые линии и эквипотенциальные поверхности электростатического поля.
Однородное электростатическое поле: 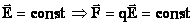 в каждой точке поля.
в каждой точке поля.
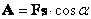
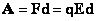 .
.
Следовательно:
Т. е. работа при перемещении заряда между двумя точками в электростатическом поле
- не зависит от формы траектории, а зависит от положения этих точек.
- равна убыли потенциальной энергии заряда в этом поле;
- работа по замкнутой траектории равна нулю.
Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
|
Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называютпотенциалом φ электрического поля:
|
Потенциал φ является энергетической характеристикой электростатического поля.
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
|
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
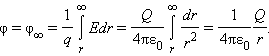 |
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.
Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
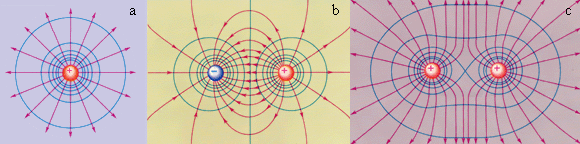 | ||||||
Рисунок 1.4.3. Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L 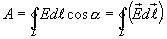 Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю. Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю. 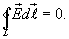 Связь между напряженностью электростатического поля и потенциалом E= - grad Связь между напряженностью электростатического поля и потенциалом E= - grad 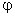 = -Ñ = -Ñ 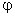 .Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность Eнаправлена в сторону убывания потенциала. .Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность Eнаправлена в сторону убывания потенциала. 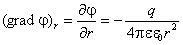 3)Электрический диполь. Электрический момент диполя. Поле диполя. 3)Электрический диполь. Электрический момент диполя. Поле диполя. 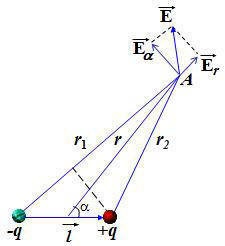 Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+q,-q), расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля. Плечо диполя — вектор Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+q,-q), расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля. Плечо диполя — вектор  , направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между зарядами. Электрический момент диполя (дипольный момент): , направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между зарядами. Электрический момент диполя (дипольный момент): 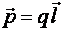 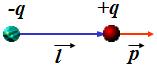 4. Проводник во внешнем электростатическом поле. Электростатическая защита. Если проводнику сообщить избыточный заряд, то этот заряд распределится по поверхности проводника. если внутри проводника выделить произвольную замкнутую поверхность S, то поток вектора напряженности электрического поля через эту поверхность должен быть равен нулю. внутри проводника будет существовать электрическое поле, что приведет к перемещению зарядов. Следовательно, для того, чтобы выполнялось условие 4. Проводник во внешнем электростатическом поле. Электростатическая защита. Если проводнику сообщить избыточный заряд, то этот заряд распределится по поверхности проводника. если внутри проводника выделить произвольную замкнутую поверхность S, то поток вектора напряженности электрического поля через эту поверхность должен быть равен нулю. внутри проводника будет существовать электрическое поле, что приведет к перемещению зарядов. Следовательно, для того, чтобы выполнялось условие 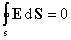 ,суммарный электрический заряд внутри этой произвольной поверхности должен равняться нулю. ,суммарный электрический заряд внутри этой произвольной поверхности должен равняться нулю. 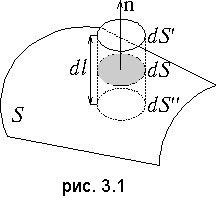 Напряженность электрического поля вблизи поверхности заряженного проводника можно определить, используя теорему Гаусса. Для этого выделим на поверхности проводника малую произвольную площадку dS и, считая ее за основание, построим на ней цилиндр с образующей dl (рис. 3.1). На поверхности проводника вектор Е направлен по нормали к этой поверхности. Поэтому поток вектора Е через боковую поверхность цилиндра из-за малости dl равен нулю. Поток этого вектора через нижнее основание цилиндра, находящееся внутри проводника, также равен нулю, так как внутри проводника электрическое поле отсутствует. Следовательно, поток вектора Е через всю поверхность цилиндра равен потоку через его верхнее основание dS': Напряженность электрического поля вблизи поверхности заряженного проводника можно определить, используя теорему Гаусса. Для этого выделим на поверхности проводника малую произвольную площадку dS и, считая ее за основание, построим на ней цилиндр с образующей dl (рис. 3.1). На поверхности проводника вектор Е направлен по нормали к этой поверхности. Поэтому поток вектора Е через боковую поверхность цилиндра из-за малости dl равен нулю. Поток этого вектора через нижнее основание цилиндра, находящееся внутри проводника, также равен нулю, так как внутри проводника электрическое поле отсутствует. Следовательно, поток вектора Е через всю поверхность цилиндра равен потоку через его верхнее основание dS': 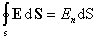 где Еn - проекция вектора напряженности электрического поля на внешнюю нормаль n к площадке dS. По теореме Гаусса, этот поток равен алгебраической сумме электрических зарядов, охватываемых поверхностью цилиндра, отнесенной к произведению электрической постоянной и относительной диэлектрической проницаемости среды, окружающей проводник. Внутри цилиндра находится заряд где Еn - проекция вектора напряженности электрического поля на внешнюю нормаль n к площадке dS. По теореме Гаусса, этот поток равен алгебраической сумме электрических зарядов, охватываемых поверхностью цилиндра, отнесенной к произведению электрической постоянной и относительной диэлектрической проницаемости среды, окружающей проводник. Внутри цилиндра находится заряд 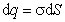 , где , где 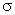 - поверхностная плотность зарядов. Следовательно - поверхностная плотность зарядов. Следовательно 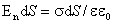 и и 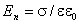 , т. е. напряженность электрического поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности электрических зарядов, находящихся на этой поверхности. Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля. Это явление связано с тем, что на поверхности проводника (заряженного или незаряженного), помещённого во внешнее электрическое поле, заряды перераспределяются так (явление электростатической индукции), что создаваемое ими внутри проводника поле полностью компенсирует внешнее. 5.1 Распределение заряда на проводнике. Электроемкость проводника. Вывод формулы электроемкости проводящей сферы. Распределение заряда в проводнике во внешнем электрическом поле Проводником называют тело, содержащее свободные носители заряда, т. е. заряды, которые под действием сколь угодно малого электрического поля перемещаются на макрорасстояния (в пределах всего проводника). Типичным примером проводника являются металлы, в которых роль свободных носителей заряда играют так называемые коллективизированные электроны. Существуют проводники, в которых роль свободных носителей заряда играют подвижные ионы. Если сумма положительных и отрицательных носителей заряда (как свободных, так и связанных) в теле равна нулю, то тело электронейтрально, в противном случае – заряжено. Равновесное распределение избыточного заряда в заряженном проводнике должно удовлетворять следующим условиям: – напряженность электрического поля внутри проводника равна нулю (следовательно, объем проводника является эквипотенциальным); – линии напряженности электрического поля вне проводника, в непосредственной близости от его поверхности, перпендикулярны этой поверхности. Отклонение от любого из перечисленных условий привело бы к перемещению свободных носителей заряда либо в объеме, либо по поверхности проводника, но это означало бы отсутствие равновесия. Поскольку напряженность электрического поля, а значит, и электрическая индукция внутри заряженного проводника в равновесии должны быть равны нулю, то и поток вектора электрической индукции через любую замкнутую поверхность, построенную внутри проводника, должен быть равен нулю. В соответствии с теоремой Гаусса это означает, что внутри вспомогательных поверхностей, т. е. в любом объеме внутри заряженного проводника, суммарный заряд равен пулю. Отсюда следует, что весь избыточный заряд в заряженном проводнике при равновесии должен располагаться только на его поверхности. Электрическая индукция (смещение) вблизи от поверхности заряженного проводника численно равна поверхностной плотности избыточного заряда. Между электрическим полем вблизи поверхности заряженного проводника и плотностью избыточного заряда на этой поверхности существует прямая связь. Поэтому судить о распределении заряда на поверхности проводника можно по густоте силовых линий, отходящих от различных участков этой поверхности. Из общих соображений можно прийти к выводу, что напряженность электрического поля заряженного проводника неправильной формы будет выше в области выступов иниже в области впадин (рис. 5.1). , т. е. напряженность электрического поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности электрических зарядов, находящихся на этой поверхности. Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля. Это явление связано с тем, что на поверхности проводника (заряженного или незаряженного), помещённого во внешнее электрическое поле, заряды перераспределяются так (явление электростатической индукции), что создаваемое ими внутри проводника поле полностью компенсирует внешнее. 5.1 Распределение заряда на проводнике. Электроемкость проводника. Вывод формулы электроемкости проводящей сферы. Распределение заряда в проводнике во внешнем электрическом поле Проводником называют тело, содержащее свободные носители заряда, т. е. заряды, которые под действием сколь угодно малого электрического поля перемещаются на макрорасстояния (в пределах всего проводника). Типичным примером проводника являются металлы, в которых роль свободных носителей заряда играют так называемые коллективизированные электроны. Существуют проводники, в которых роль свободных носителей заряда играют подвижные ионы. Если сумма положительных и отрицательных носителей заряда (как свободных, так и связанных) в теле равна нулю, то тело электронейтрально, в противном случае – заряжено. Равновесное распределение избыточного заряда в заряженном проводнике должно удовлетворять следующим условиям: – напряженность электрического поля внутри проводника равна нулю (следовательно, объем проводника является эквипотенциальным); – линии напряженности электрического поля вне проводника, в непосредственной близости от его поверхности, перпендикулярны этой поверхности. Отклонение от любого из перечисленных условий привело бы к перемещению свободных носителей заряда либо в объеме, либо по поверхности проводника, но это означало бы отсутствие равновесия. Поскольку напряженность электрического поля, а значит, и электрическая индукция внутри заряженного проводника в равновесии должны быть равны нулю, то и поток вектора электрической индукции через любую замкнутую поверхность, построенную внутри проводника, должен быть равен нулю. В соответствии с теоремой Гаусса это означает, что внутри вспомогательных поверхностей, т. е. в любом объеме внутри заряженного проводника, суммарный заряд равен пулю. Отсюда следует, что весь избыточный заряд в заряженном проводнике при равновесии должен располагаться только на его поверхности. Электрическая индукция (смещение) вблизи от поверхности заряженного проводника численно равна поверхностной плотности избыточного заряда. Между электрическим полем вблизи поверхности заряженного проводника и плотностью избыточного заряда на этой поверхности существует прямая связь. Поэтому судить о распределении заряда на поверхности проводника можно по густоте силовых линий, отходящих от различных участков этой поверхности. Из общих соображений можно прийти к выводу, что напряженность электрического поля заряженного проводника неправильной формы будет выше в области выступов иниже в области впадин (рис. 5.1). 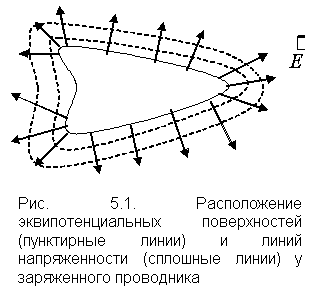
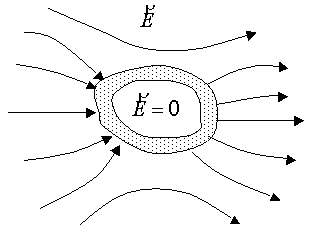
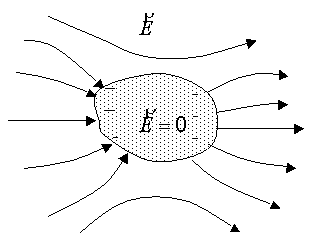
При внесении проводника во внешнее электрическое поле свободные носители заряда, присущие проводнику, смещаются по полю (если они положительные) и против поля (если они отрицательные). Этот процесс идет до тех пор, пока на поверхности проводника не образуются смещенные заряды, собственное поле которых полностью экранирует внешнее электрическое поле (в результате поле внутри проводника будет равно нулю). Установление равновесного распределения заряда происходит чрезвычайно быстро, например, для металлов это время может составлять всего 10–19 с. Заряды, возникающие на поверхности проводника при внесении его во внешнее электростатическое поле, называются индуцированными, а само явление разделения и смещения зарядов в проводнике – электризацией через влияние. Поскольку электрическое поле в проводнике, находящемся во внешнем электростатическом поле, равно нулю, то его объем, включая поверхность, является эквипотенциальным. Это означает, что силовые линии напряженности электрического поля, подходящие к проводнику, должны быть нормальны к его поверхности и оканчиваться или начинаться на ней, не проникая внутрь проводника (рис. 5.2, а). Введение проводника в электрическое поле приводит в общем случае к перераспределению электрического поля в пространстве, проявляющегося в изменении вида силовых линий.
Рис. 52. Сплошной проводник (а) и замкнутая проводящая оболочка (б)во внешнем электростатическом поле Если из проводника, находящегося во внешнем электрическом поле, удалить внутреннюю (электронейтральную) часть, т. е. образовать внутри полость, то это никак не отразится на величине и пространственном распределении электрического поля. В частности, внутри полости поле будет равным нулю (рис. 5.2, б). Таким образом, внешние по отношению к оболочке заряды не могут создавать внутри оболочки электрическое поле (или иначе – внешние электрические поля не проникают внутрь замкнутой проводящей оболочки). На этом принципе основана так называемая электростатическая защита. Чтобы предохранить какие-либо тела, например, измерительные приборы, от влияния внешних электрических полей, их окружают проводящей оболочкой. На практике достаточно эффективную защиту от внешних электростатических полей удается получить, используя вместо сплошной проводящей оболочки проводящую сетку. |
Электрическая емкость тел
Рассмотрим сначала уединенный заряженный проводник (т. е. проводник, расстояние от которого до других проводников столь велико, что их влиянием можно пренебречь). Избыточный заряд распределен по поверхности проводника, причем плотность поверхностного заряда зависит от радиуса кривизны этой поверхности. Тем не менее из общих соображений понятно, что чем выше будет заряд проводника, тем больше поверхностная плотность заряда в некотором произвольно выбранном месте проводника. Но чем выше поверхностная плотность заряда, тем больше будет напряженность электрического поля вблизи проводника, а значит, тем большую работу надо совершить (либо тем большую работу совершит поле), чтобы переместить пробный заряд от этой поверхности в бесконечность (т. е. тем выше будет потенциал поверхности). Таким образом, между зарядом проводника и его потенциалом существует прямая связь, которую можно представить в виде:
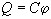 . (5.1)
. (5.1)
Коэффициент пропорциональности в (5.1) является характеристикой электрических свойств уединенного тела, так называемой электрической емкостью, которую можно определить следующим образом:
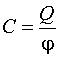 . (5.2)
. (5.2)
Электроемкость уединенного проводника численно равна величине заряда, который надо сообщить проводнику, чтобы повысить его потенциал на единицу.
Электроемкость уединенного проводника зависит от формы и размеров проводника, а также от диэлектрической проницаемости окружающей среды.
Единицей измерения электроемкости в СИ является 1 фарада.
Если взять в качестве проводящего шара земной шар (R = 6,4?106 м), то его емкость оказывается равной ~7?10–4 Ф. Таким образом, единица измерения емкости в СИ 1 фарада является очень большой величиной и на практике в качестве единиц измерения используют 1 мкФ = 10–6 Ф, 1 нФ = 10–9 Ф, 1пФ = 10 –12 Ф.
Электрической емкостью обладают не только проводники, но и все тела: диэлектрики, полупроводники, жидкости.
Рис. 5.3 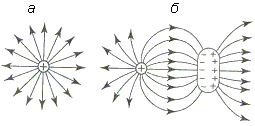 . Проводник, внесенный в электрическое поле другого заряженного проводника, меняет это поле за счет электризации через влияние: а – исходное поле; б – поле после внесения проводника . Проводник, внесенный в электрическое поле другого заряженного проводника, меняет это поле за счет электризации через влияние: а – исходное поле; б – поле после внесения проводника |
Поскольку емкость тела обратно пропорциональна величине потенциала этого тела (при фиксированном заряде тела), то отмеченное выше изменение потенциалазаряженного тела при внесении проводника приведет к увеличению электроемкости тела.
Существенное влияние окружения на величину электроемкости отдельного заряженного проводника не позволяет на практике использовать отдельные проводники в качестве элементов постоянной емкости в электро- и радиотехнических устройствах.
В отличие от отдельного проводника, система двух разноименно заряженных проводников, расположенных на небольшом расстоянии друг от друга, имеет электрическое поле, практически полностью сосредоточенное между этими проводниками и поэтому слабо зависящее от внешнего окружения.
Система двух проводников, при разноименном заряжении которых образуется электростатическое поле, практически не выходящее за пределы этой системы, называется электрическим конденсатором.
Рассуждения, аналогичные описанным ранее, для уединенного проводника позволяют сделать вывод о том, что разность потенциалов между обкладками конденсатора оказывается прямо пропорциональной величине заряда на одной из этих обкладок. Таким образом, можно ввести понятие электрической емкости конденсатора:
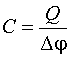 . ( 5.3 )
. ( 5.3 )
Емкость конденсатора численно равна заряду на одной из разноименно заряженных обкладок конденсатора, разность потенциалов между которыми равна единице.
Емкость плоского конденсатора, состоящего из двух металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга,
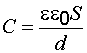 , (5.4)
, (5.4)
где 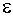 – диэлектрическая проницаемость среды.
– диэлектрическая проницаемость среды.
Емкость цилиндрического конденсатора
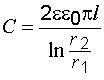 , (5.5)
, (5.5)
где 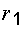 и
и 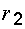 – радиусы двух полых коаксиальных цилиндрических обкладок;
– радиусы двух полых коаксиальных цилиндрических обкладок; 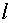 – длина обкладок.
– длина обкладок.
Емкость сферического конденсатора
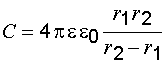 , (5.6)
, (5.6)
где 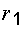 и
и 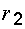 – радиусы сферических обкладок конденсатора.
– радиусы сферических обкладок конденсатора.
Конденсаторы изготовляют для разных целей. В некоторых электрических цепях применение конденсаторов позволяет пропускать быстрые изменения потенциалов, но задерживать их медленные изменения. (Иначе говоря, переменный ток может проходить через конденсаторы, в то время как постоянный – не может). В других устройствах конденсаторы используются для того, чтобы накапливать на короткое время заряд, или электрическую энергию.
В конденсаторах, используемых в электрических цепях для накопления энергии, обычно играют роль один или два фактора, определяющих емкость.Например, бумажный, или станиолевый конденсатор состоит из туго свернутых тонких лент фольги и парафинированной бумаги, сложенных вместе. Полнаяплощадь поверхности очень велика, а расстояние между лентами фольги, служащими обкладками конденсатора, равно толщине изолирующей бумаги или пластмассы.
В электролитических конденсаторах площадь поверхности фольги не очень велика, но расстояние между обкладками d определяется химической пленкой, которая может быть толщиной всего в 10 или 100 атомов. Поскольку d настолько мала, то электрическая емкость может быть очень большой. Однако в этом случае тонкая химическая пленка сохраняется, только пока электрическое поле направлено в определенную сторону.
Сферический конденсатор состоит из двух концентрических металлических обкладок А и В сферической формы, радиусы которых соответственно равны r1 и r2 (рис.1). Пусть q >0 — заряд обкладки А, а -q — обкладки В. Равномерно заряженная сфера создает электростатическое поле только в области пространства, лежащей вне этой сферы. Вне конденсатора поля разноименно заряженных обкладок А и В взаимно уничтожаются, а поле в области между обкладками создается только зарядом обкладки А. Поэтому разность потенциалов между обкладками:
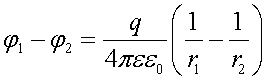 Подставив в формулу для емкости значение φ1-φ2, получим
Подставив в формулу для емкости значение φ1-φ2, получим
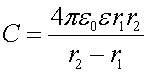
При r2→∞ внутреннюю обкладку сферического конденсатора можно рассматривать как уединенный шар. В этом случае 1/r2→0 и формула для сферического конденсатора совпадает с формулой для уединенной сферы:
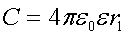
При любом конечном значении r2 >r1
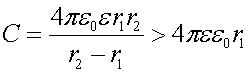
то есть электроемкость сферического конденсатора больше электроемкости уединенного шара радиуса r1.
Если r2-r1=l<<r1, то можно считать r2≈r1. Тогда
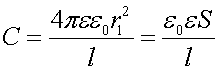
5.2 Диэлектрики во внешнем электростатическом поле. Поляризация диэлектриков. Вектор поляризованности. Условия на границе 2-х диэлектриков.Проводники и диэлектрики в электрическом полеВещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в среднем по объемам, включающим большое число атомов или молекул, равно нулю. При наличии внешнего поля происходит перераспределение заряженных частиц, и в веществе возникает собственное электрическое поле. Полное электрическое поле 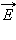 складывается в соответствии с принципом суперпозиции из внешнего поля
складывается в соответствии с принципом суперпозиции из внешнего поля 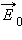 и внутреннего поля
и внутреннего поля 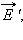 создаваемого заряженными частицами вещества.
создаваемого заряженными частицами вещества.
Вещество многообразно по своим электрическим свойствам. Наиболее широкие классы вещества составляют проводники и диэлектрики.
Основная особенность проводников – наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника. Типичные проводники – металлы.
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды (рис. 1.5.1). Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды –индукционными зарядами.
Индукционные заряды создают свое собственное поле 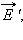 которое компенсирует внешнее поле
которое компенсирует внешнее поле 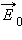 во всем объеме проводника:
во всем объеме проводника: 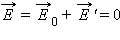 (внутри проводника).
(внутри проводника).
Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника.
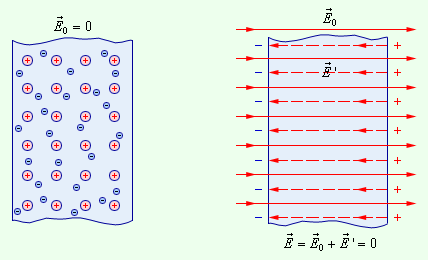 |
| Рисунок 1.5.1. Электростатическая индукция |
Все внутренние области проводника, внесенного в электрическое поле, остаются электронейтральными. Если удалить некоторый объем, выделенный внутри проводника, и образовать пустую полость, то электрическое поле внутри полости будет равно нулю. На этом основана электростатическая защита – чувствительные к электрическому полю приборы для исключения влияния поля помещают в металлические ящики (рис. 1.5.2).
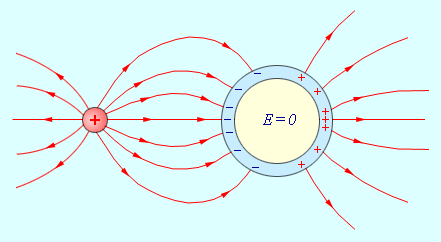 |
| Рисунок 1.5.2. Электростатическая защита. Поле в металлической полости равно нулю |
Так как поверхность проводника является эквипотенциальной, силовые линии у поверхности должны быть перпендикулярны к ней.
В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
При внесении диэлектрика во внешнее электрическое поле 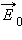 в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.
в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.
Связанные заряды создают электрическое поле 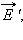 которое внутри диэлектрика направлено противоположно вектору напряженности
которое внутри диэлектрика направлено противоположно вектору напряженности 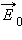 внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле
внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле 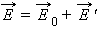 внутри диэлектрика оказывается по модулю меньше внешнего поля
внутри диэлектрика оказывается по модулю меньше внешнего поля 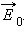
Физическая величина, равная отношению модуля напряженности 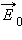 внешнего электрического поля в вакууме к модулю напряженности
внешнего электрического поля в вакууме к модулю напряженности 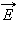 полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.
полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.
|
Существует несколько механизмов поляризации диэлектриков. Основными из них являются ориентационная и электронная поляризации. Эти механизмы проявляются главным образом при поляризации газообразных и жидких диэлектриков.
Ориентационная или дипольная поляризация возникает в случае полярных диэлектриков, состоящих из молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы представляют собой микроскопические электрические диполи – нейтральную совокупность двух зарядов, равных по модулю и противоположных по знаку, расположенных на некотором расстоянии друг от друга. Дипольным моментом обладает, например, молекула воды, а также молекулы ряда других диэлектриков (H2S, NO2 и т. д.).
При отсутствии внешнего электрического поля оси молекулярных диполей из-за теплового движения ориентированы хаотично, так что на поверхности диэлектрика и в любом элементе объема электрический заряд в среднем равен нулю.
При внесении диэлектрика во внешнее поле 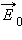 возникает частичная ориентация молекулярных диполей. В результате на поверхности диэлектрика появляются нескомпенсированные макроскопические связанные заряды, создающие поле
возникает частичная ориентация молекулярных диполей. В результате на поверхности диэлектрика появляются нескомпенсированные макроскопические связанные заряды, создающие поле 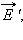 направленное навстречу внешнему полю
направленное навстречу внешнему полю 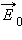 (рис. 1.5.3).
(рис. 1.5.3).
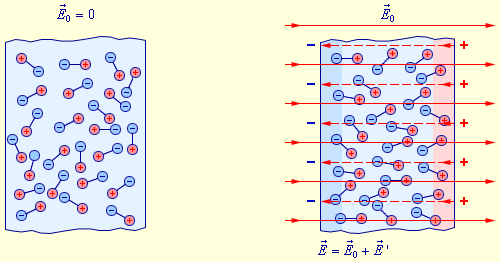 |
| Рисунок 1.5.3. Ориентационный механизм поляризации полярного диэлектрика |
Поляризация полярных диэлектриков сильно зависит от температуры, так как тепловое движение молекул играет роль дезориентирующего фактора.
Электронный или упругий механизм проявляется при поляризации неполярных диэлектриков, молекулы которых не обладают в отсутствие внешнего поля дипольным моментом. Под действием электрического поля молекулы неполярных диэлектриков деформируются – положительные заряды смещаются в направлении вектора 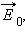 а отрицательные – в противоположном направлении. В результате каждая молекула превращается в электрический диполь, ось которого направлена вдоль внешнего поля. На поверхности диэлектрика появляются нескомпенсированные связанные заряды, создающие свое поле
а отрицательные – в противоположном направлении. В результате каждая молекула превращается в электрический диполь, ось которого направлена вдоль внешнего поля. На поверхности диэлектрика появляются нескомпенсированные связанные заряды, создающие свое поле 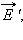 направленное навстречу внешнему полю
направленное навстречу внешнему полю 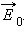 Так происходит поляризация неполярного диэлектрика (рис. 1.5.4).
Так происходит поляризация неполярного диэлектрика (рис. 1.5.4).
Деформация неполярных молекул под действием внешнего электрического поля не зависит от их теплового движения, поэтому поляризация неполярного диэлектрика не зависит от температуры. Примером неполярной молекулы может служить молекула метана CH4. У этой молекулы четырехкратно ионизированный ион углерода C4–располагается в центре правильной пирамиды, в вершинах которой находятся ионы водорода H+. При наложении внешнего электрического поля ион углерода смещается из центра пирамиды, и у молекулы возникает дипольный момент, пропорциональный внешнему полю.
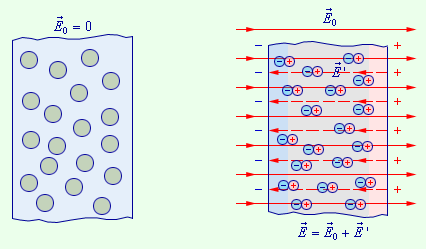 |
| Рисунок 1.5.4. Поляризация неполярного диэлектрика |
Электрическое поле 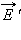 связанных зарядов, возникающее при поляризации полярных и неполярных диэлектриков, изменяется по модулю прямо пропорционально модулю внешнего поля
связанных зарядов, возникающее при поляризации полярных и неполярных диэлектриков, изменяется по модулю прямо пропорционально модулю внешнего поля 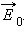 В очень сильных электрических полях эта закономерность может нарушаться, и тогда проявляются различные нелинейные эффекты. В случае полярных диэлектриков в сильных полях может наблюдаться эффект насыщения, когда все молекулярные диполи выстраиваются вдоль силовых линий. В случае неполярных диэлектриков сильное внешнее поле, сравнимое по модулю с внутриатомным полем, может существенно деформировать атомы или молекулы вещества и изменить их электрические свойства. Однако, эти явления практически никогда не наблюдаются, так как для этого нужны поля с напряженностью порядка 1010–1012 В/м. Между тем, гораздо раньше наступает электрический пробой диэлектрика.
В очень сильных электрических полях эта закономерность может нарушаться, и тогда проявляются различные нелинейные эффекты. В случае полярных диэлектриков в сильных полях может наблюдаться эффект насыщения, когда все молекулярные диполи выстраиваются вдоль силовых линий. В случае неполярных диэлектриков сильное внешнее поле, сравнимое по модулю с внутриатомным полем, может существенно деформировать атомы или молекулы вещества и изменить их электрические свойства. Однако, эти явления практически никогда не наблюдаются, так как для этого нужны поля с напряженностью порядка 1010–1012 В/м. Между тем, гораздо раньше наступает электрический пробой диэлектрика.
У многих неполярных молекул при поляризации деформируются электронные оболочки, поэтому этот механизм получил название электронной поляризации. Этот механизм является универсальным, поскольку деформация электронных оболочек под действием внешнего поля происходит в атомах, молекулах и ионах любого диэлектрика.
В случае твердых кристаллических диэлектриков наблюдается так называемая ионная поляризация, при которой ионы разных знаков, составляющие кристаллическую решетку, при наложении внешнего поля смещаются в противоположных направлениях, вследствие чего на гранях кристалла появляются связанные (нескомпенсированные) заряды. Примером такого механизма может служить поляризация кристалла NaCl, в котором ионы Na+ и Cl– составляют две подрешетки, вложенные друг в друга. В отсутствие внешнего поля каждая элементарная ячейка кристалла NaCl (см. Часть I § 3.6 ) электронейтральна и не обладает дипольным моментом. Во внешнем электрическом поле обе подрешетки смещаются в противоположных направлениях, т. е. кристалл поляризуется.
При поляризации неоднородного диэлектрика связанные заряды могут возникать не только на поверхностях, но и в объеме диэлектрика. В этом случае электрическое поле 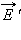 связанных зарядов и полное поле
связанных зарядов и полное поле 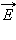 могут иметь сложную структуру, зависящую от геометрии диэлектрика. Утверждение о том, что электрическое поле
могут иметь сложную структуру, зависящую от геометрии диэлектрика. Утверждение о том, что электрическое поле 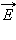 в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем
в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем 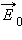 строго справедливо только в случае однородного диэлектрика, заполняющего все пространство, в котором создано внешнее поле. В частности:
строго справедливо только в случае однородного диэлектрика, заполняющего все пространство, в котором создано внешнее поле. В частности:
Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд Q, то напряженность поля 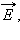 создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:
создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:
|
ВЕКТОР ПОЛЯРИЗАЦИИ
Вектор поляризации — векторная физическая величина, равная дипольному моменту единицы объёма вещества, возникающему при его поляризации, количественная характеристика диэлектрической поляризации.
Обозначается буквой 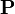 , в Международной системе единиц (СИ) измеряется в Кл/м2
, в Международной системе единиц (СИ) измеряется в Кл/м2
Диэлектрическая поляризация обусловлена смещением связанных зарядов вещества во внешнем электрическом поле относительно их расположения при отсутвии внешнего электрического поля. Если выделить какой либо объём в диэлектрике, то в результате приложения поля на его поверхности могут возникнуть поверхностные электрические заряды 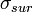 . Такие заряды могут возникнуть или благодаря смещению электронной оболочки относительно ядра атома, или же в результате переориентации молекул, которые имеют собственный дипольный момент.
. Такие заряды могут возникнуть или благодаря смещению электронной оболочки относительно ядра атома, или же в результате переориентации молекул, которые имеют собственный дипольный момент.
Нормальную к поверхности составляющую вектора поляризации определяют как
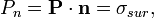
где 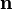 — орт нормали к поверхности.
— орт нормали к поверхности.
Можно ввести вектор электрической индукции 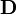 , который удобен при описании электрического поля в сплошной среде:
, который удобен при описании электрического поля в сплошной среде:
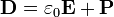 (СИ)
(СИ)
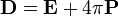 (СГС)
(СГС)