Деформативность каменной кладки при сжатии. Модуль упругости , деформация кладки . Упругая характеристика кладки

ДЕФОРМАТИВНЫЕ СВОЙСТВА КАМЕННОЙ КЛАДКИ

Каменная кладка деформируется как упругопластический материал. Полная деформация состоит из упругой и пластической составляющих. В течение первых трех лет рост пластической деформации затухает, если напряжения в кладке не превышают 80…90 % от прочности кладки. В противном случае происходит ее разрушение.

При испытании кладки загружением до разрушения получают график зависимости напряжений от деформаций (рис. 5).

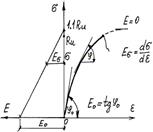
Рис. 5. График деформаций кладки

При малых напряжениях график прямолинеен, а напряжения можно получить по деформациям через модуль упругости (начальный модуль деформаций):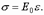

При повышении напряжений график искривляется, и модуль деформации кладки 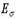уменьшается 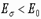. Если график экстраполировать после момента разрушения кладки до точки, где 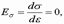то на оси ординат напряжения будут примерно равны 1.1Ru.

По предложению Л.И. Онищика в нормах принята линейная зависимость модуля деформаций от напряжений (см. рис. 5):

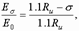откуда .

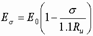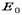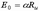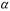Начальный модуль упругости может быть выражен через предел прочности: , где – упругая характеристика кладки, зависящая от вида кладки и марки раствора [1, табл. 15].

Например, при марках раствора М25 … М200:

а) для кладки из кирпича глиняного пластического прессования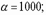

б) для кладки из силикатного кирпича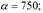

в) для кладки из крупных бетонных блоков .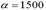

В соответствии с [1] модуль деформации кладки 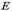должен приниматься:

а) для определения усилий в кладке при расчете конструкций по прочности кладки

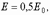где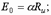

б) при определении деформаций кладки, периода колебаний и жесткости каменных конструкций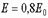

36. Расчёт прочности каменных конструкций при осевом сжатии.

4. РАСЧЕТ КАМЕННЫХ КОНСТРУКЦИЙ НА ЦЕНТРАЛЬНОЕ СЖАТИЕ

К центрально сжатым относятся внутренние столбы и простенки каменных зданий.

Расчет выполняется по формуле [1, (10)]

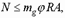
где 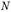– усилие от расчетных нагрузок; 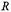– расчетное сопротивление сжатию кладки, определяемое в зависимости от вида кладки, марки камня и раствора по [1, табл. 2–9]; 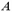площадь сечения элемента; 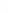– коэффициент продольного изгиба, зависящий от гибкости 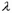и упругой характеристики кладки ; 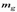– коэффициент, учитывающий влияние на прочность длительного действия нагрузки

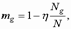
где 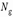и 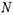– усилия от длительной и полной нагрузки соответственно;
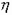– коэффициент, зависящий от гибкости сжатого элемента 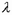и вида кладки, определяемый по [1, табл. 20]. При высоте сечения элемента 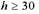см или радиусе инерции сечения 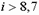см коэффициент .

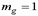37. Расчёт прочности каменных конструкций при

внецентренном сжатии.

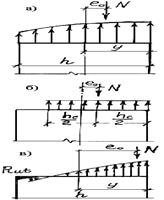
Рис. 11. Напряженные состояния внецентренно загруженной кладки

1. РАСЧЕТ ВНЕЦЕНТРЕННО СЖАТЫХ КАМЕННЫХ ЭЛЕМЕНТОВ

На внецентренное сжатие работают элементы каменных конструкций: наружные стены, простенки и столбы гражданских и промышленных зданий, стены подвалов, карнизные участки стен.

Предпосылки расчета

1. При малых эксцентриситетах все сечение сжато (рис. 11, а).

Для упрощения расчетов криволинейную эпюру заменяют прямоугольной (рис. 11, б). При этом центр тяжести эпюры совмещают с местом приложения силы.

2. С увеличением эксцентриситета в сечении возникает растяжение, и появляются трещины (рис. 11, в). Появление трещин не приводит элемент к разрушению, если величина напряжений в сжатой зоне не превышает предельной. Современные методы расчета оценивают несущую способность кладки по нагрузке, разрушающей сжатую зону, а не по нагрузке появления трещин.

3. При толщине стены 25 см и менее учитывается случайный эксцентриситет 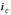, который суммируется с эксцентриситетом силы :

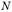для несущих стен 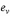= 2 см;

для самонесущих стен 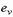= 1 см.

для ненесущих стен и перегородок 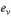= 0.

4. При больших эксцентриситетах ( 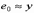) в элементах без продольной растянутой арматуры сжатая зона может оказаться настолько малой, что при случайном увеличении 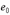усилие 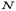выйдет за пределы сечения и произойдет мгновенное разрушение элемента.

Поэтому эксцентриситеты ограничиваются:

для основных сочетаний усилий 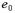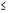0.9 у;

для особых сочетаний усилий 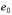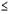0.95 у.

Если толщина стены 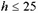см:

для основных сочетаний усилий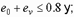

для особых сочетаний усилий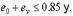

Кроме того, для несущих стен и столбов должно выполняться условие

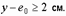
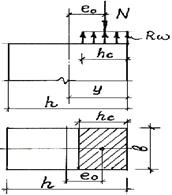
Рис. 12. К расчету кладки на внецентренное сжатие

5. При 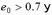необходимо выполнить расчет по раскрытию трещин в швах кладки.

На основании рассмотренных предпосылок расчетная схема при прямоугольной форме сжатой зоны будет иметь вид, показанный на рис. 12.

Расчет кладки производится по формуле [1, (13)]

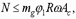
где 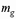– коэффициент, учитывающий влияние на прочность длительно действующей нагрузки,

,

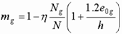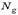– усилие от длительных нагрузок;
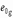– эксцентриситет от силы 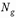; 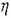– коэффициент, зависящий от гибкости и вида кладки, определяемый по [1, табл. 20]. Если высота сечения элемента 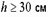или радиус инерции сечения 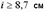, коэффициент 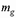следует принимать равным единице; 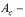площадь сжатой зоны сечения, определяемая из условия, что ее центр тяжести совпадает с точкой приложения расчетной продольной силы 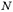. При прямоугольной форме сжатой зоны сечения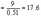 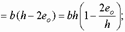при любой форме сжатой зоны сечения положение границы площади 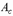определяется из условия равенства нулю статического момента этой площади относительно ее центра тяжести; 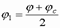– коэффициент продольного изгиба при внецентренном сжатии; 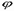– коэффициент продольного изгиба при центральном сжатии для всего сечения в плоскости момента, определенный по расчетной высоте элемента 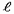[1, табл. 18]; 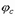– коэффициент продольного изгиба при центральном сжатии для сжатой части сечения,
определяемый по фактической высоте элемента 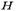[1, табл. 18] в плоскости момента при гибкост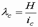и (или 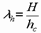), где 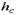и 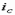– высота и радиус инерции сжатой части сечения 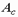в плоскости момента.

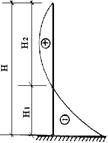
Рис. 13. К расчету на моменты разных знаков

При знакопеременной эпюре изгибающего момента по высоте элемента проверку прочности следует производить в сечениях с максимальными моментами различных знаков.

Коэффициент продольного изгиба 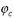определятся по высоте части элемента в пределах однозначной эпюры изгибающего момента при гибкостях:

а) при расчете нижней части элемента (рис. 13)

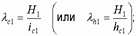
б) для верхней части элемента:

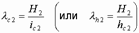
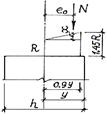
Рис. 14. К расчету коэффициента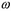

В формуле [1, (13)] 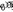– расчетное сопротивление кладки при центральном сжатии.

Коэффициент 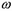учитывает эффект обоймы, повышающий прочность кладки с ростом

эксцентриситета 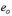. В расчете принято, что при максимальном эксцентриситете 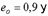прочность кладки возрастает на 45 %. Определим величину коэффициента 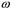из условия подобия треугольников графика на рис. 14:

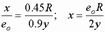
Расчетное сопротивление кладки при внецентренном сжатии

,

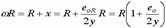где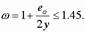

Для прямоугольного сечения, пр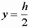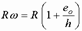и

и .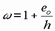

Внецентренно сжатые элементы из плоскости действия момента должны проверяться на центральное сжатие.