Статистическая обработка результатов анализа при нормальном распределении
Расчет результатов анализа требует правильной записи исходных данных, проверки наличия дрейфа и выявления грубых промахов. После вычисления результаты усредняют, округляют и представляют в форме доверительных интервалов. Полученные результаты часто сопоставляют друг с другом или с некоторыми постоянными величинами (нормативами). На каждой из перечисленных стадий используют статистические алгоритмы. Их выбор зависит от характера распределения данных, т. е. от методики анализа. Так, если известно, что результаты подчиняются распределению Пуассона, то отбраковку промахов и расчет доверительных интервалов ведут иными способами, чем при нормальном распределении. Далее будет рассмотрен наиболее важный случай – обработка нормально распределенных данных. Если характер распределения неизвестен, результаты анализа обрабатывают с применением более сложных статистических алгоритмов (робастные методы, непараметрические критерии), описанных в специальной литературе.
Запись исходных данных. Немедленно после любого прямого измерения (взвешивания, титрования, фотометрирования, измерения потенциала и т. п.) его результат должен быть записан в лабораторный журнал. Нельзя субъективно отбирать результаты (записывать одни, которые представляются «правильными», и не записывать другие). Не принято также отмечать «более надежные» и «менее надежные» результаты измерений, все варианты одной выборки (например, объемы титранта, затраченные на повторные титрования) должны учитываться в одинаковой степени. Это важное условие называет условием равноточности.
Результаты прямых измерений записывают так, чтобы предпоследняя цифра не вызывала сомнений, а последняя – соответствовала абсолютной погрешности (D) данного измерения. Так, если объем титранта записан в виде 24 мл, это означает, что измерение проведено с погрешностью 1 мл; если же пользовались более точными приборами с погрешностью 0,1 мл, запись должна быть сделана в виде 24,0 мл, с тремя значащими цифрами.
Значащими называют все достоверно известные цифры в числовом результате измерения, а также первую из недостоверных. В правильно записанном результате измерения значащими являются все цифры, кроме 0, а также 0, если он стоит после других значащих цифр. Не следует путать число значащих цифр и число десятичных знаков (цифр, стоящих после запятой). При подсчете количества значащих цифр положение запятой не имеет значения. Так, в числе 0,0020 две значащие цифры и четыре десятичных знака, а в числе 200 – три значащих цифры и нет десятичных знаков. При подобных подсчетах не учитываются цифры в степенных множителях, например, в числе 6,023·1023 – четыре значащих цифры. Очень большие и очень малые величины рекомендуется записывать именно в таком виде.
Число значащих цифр характеризует относительную погрешность измерений. Если результаты измерений записаны правильно, то, сопоставляя записи по числу значащих цифр, можно выделить более точные и менее точные данные. Возможно даже сопоставление разнородных величин, например, значений объема, массы и силы тока. Чем больше значащих цифр, тем ниже относительная погрешность и, следовательно, тем точнее соответствующие данные. Одна значащая цифра указывает, что соответствующая величина измерена с относительной погрешностью от 10 до 100 %; две значащие цифры указывают на относительную погрешность от 1 до 10 %; три – от 0,1 до 1 % и т. д. Разумеется, записывая результат титрования или взвешивания, нельзя ни прибавлять лишние значащие цифры, ни терять точность измерений из-за необоснованных округлений.
Результаты всех измеренийзаписывают в лабораторный журнал в порядке их получения. Если данные получены при многократном измерении свойств одной и той же пробы, или при исследовании множества однотипных проб, относящихся к одному и тому же объекту («параллельные пробы»), следует проверить, не наблюдается ли дрейф результатов. Но для достоверного вывода о наличии дрейфа нужно иметь выборку большого объема (7 и более вариант) и применять специальные статистические алгоритмы. Получив же результаты трех последовательных титрований – 19,9; 19,8 и 19,7 мл – нельзя считать, что методика дает дрейф, для такого вывода слишком мало данных! Если наличие дрейфа доказано с требуемой надежностью, то проводить статистическую обработку результатов нельзя. Нужно найти причину дрейфа, устранить ее, а затем повторить анализ.
Выявление и отбраковка грубых промахов. В полученной выборке всегда вызывают сомнения наименьший и наибольший результаты – не грубые ли это промахи? Существуют специальные алгоритмы для проверки наличия грубых промахов. Их выбирают в зависимости от того, по какому закону распределены варианты генеральной совокупности (все возможные результаты измерений данной величины по данной методике). Учитывают также, сколько вариант входит в имеющуюся в распоряжении аналитика выборку, известно ли стандартное отклонение для данной методики измерений, а также другие факторы. Надежность любой методики отбраковки промахов тем выше, чем больше вариант было в выборке. Если при повторных измерениях получено не менее 5 вариант, причем известно, что варианты распределены нормально, а стандартное отклонение методики неизвестно – отбраковку промахов проводят с помощью Q-теста. Для проверки сомнительной варианты х1 (наименьшего результата) рассчитывают Qэксп по формуле:
Qэксп =  . (2.7)
. (2.7)
При проверке сомнительной варианты xn (наибольшего результата) пользуются формулой:
Qэксп =  , (2.8)
, (2.8)
где xn и x1 – крайние варианты в ранжированной выборке, а x2 и xn–1 – варианты, ближайшие к ним. Сомнительная варианта (х1 или xn) отбрасывается, если по абсолютной величине Qэксп оказывается больше, чем Qтабл для желаемой надежности вывода (P) и данного числа вариант (n). Обычно используется значение P = 0,95. Если же Qэксп < Qтабл, считают, что с требуемой надежностью промах не выявлен, и сомнительную варианту оставляют.
Пример 2.4. Рассмотрим выборку 19,7; 20,6; 19,8; 19,7; 19,9; 19,6. Есть ли здесь промахи?
Решение. Сомнения вызывает вторая, наибольшая варианта. По формуле (2.8) Qэксп = (20,6 – 19,9) / (20,6 – 19,6) = 0,7 / 1,0 = 0,7. Воспользовавшись статистическими таблицами, находим Qтабл. Для n = 6 и P = 0,95 значение Qтабл равно 0,64. Следовательно, с надежностью 0,95 можно считать второе титрование ошибочным, а его результат – грубым промахом. Отбраковка промаха приведет к изменению среднего результата титрования и другому значению стандартного отклонения.
Если в одной и той же выборке одновременно присутствуют два промаха, то выявить их с помощью Q-теста обычно не удается. В таких случаях рекомендуется использовать более строгие критерии, например, пользоваться методом максимальных относительных отклонений. Подсчитывают, на сколько выборочных стандартных отклонений отстоит от среднего арифметического каждая из сомнительных вариант. Варианты, для которых отношение (х – 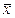 )/s превысят некоторое критическое (табличное) значение, учитывающее объем выборки и требуемую надежность вывода, считают грубыми промахами и отбрасывают. Этот критерий, как и Q-тест, применим лишь к тем выборкам, которые отвечают нормальному распределению. Статистические критерии такого типа называют параметрическими.
)/s превысят некоторое критическое (табличное) значение, учитывающее объем выборки и требуемую надежность вывода, считают грубыми промахами и отбрасывают. Этот критерий, как и Q-тест, применим лишь к тем выборкам, которые отвечают нормальному распределению. Статистические критерии такого типа называют параметрическими.
В аналитическом контроле технологических процессов, в отличие от научных исследований, по экономическим соображениям не проводят большого числа повторных измерений, не анализируют множество параллельных проб одного материала. Как правило, ограничиваются двумя измерениями. Выявить, не является ли одно из двух полученных значений х грубым промахом, нельзя ни с помощью Q-теста, ни с помощью других критериев. Но можно воспользоваться тем, что воспроизводимость измерений по данной методике известна. Она оценивается стандартным отклонением (s), указанным в описании методики или установленным при аттестации методики. Надо определить, на сколько единиц s отличаются обе полученные варианты. При нормальном распределении вероятность случайного расхождения вариант больше чем на 4s очень мала (< 0,05). Если реальное отличие двух результатов анализа окажется больше 4s, одну из вариант следует считать грубым промахом. Появление «несовместимых» вариант не дает оснований отбраковать какую-то из них, но указывает на необходимость повторения анализа. Тогда, получив еще несколько вариант, можно будет определить, какое из первоначальных измерений дало грубый промах, и отбросить соответствующий результат. Иногда критерий совместимости (4s) заменяют более строгим (6s) или менее строгим (3s). В описании же методики анализа обычно выражают этот критерий прямо в единицах измеряемой величины, даже не указывая s. Например, пишут: «если результаты определения ванадия, найденные при анализе двух параллельных проб одной и той же стали, отличаются менее чем на 0,1 % (абс.), то их среднее арифметическое считают равным действительному содержанию ванадия. Если же отличие полученных результатов больше 0,1 %, то необходимо проанализировать еще две-три пробы, а затем выявить и отбраковать грубый промах».
При дальнейшем изложении будем предполагать, что в исходных данных грубые промахи уже выявлены и исключены.
Округление результатов расчета. Результат анализа, вычисленный с помощью калькулятора или компьютера, округляют, чтобы точность результата расчета соответствовала бы точности исходных данных. Округление ведут по общепринятым математическим правилам, но, определяя степень округления, руководствуются следующими рекомендациями:
при сложении и вычитании в результате расчета оставляют столько десятичных знаков, сколько их было в самом неточном слагаемом. Например, 20,3402 г + 0,12 г » 20,46 г. Здесь одно из слагаемых было известно с точностью до четвертого десятичного знака, до 0,0001 г, а другое, менее точно определенное, – лишь до второго, до 0,01 г, поэтому и сумму округляют до второго знака, до сотых долей грамма.
при умножении и делении в результате расчета оставляют столько значащих цифр, сколько их было в наименее точном из исходных сомножителей (содержащем наименьшее число значащих цифр). Например, 25,1645 г / 25,0 мл » 1,01 г/мл. Частное округлено до трех значащих цифр, посколько столько их было в делителе. Если в качестве сомножителей используют постоянные коэффициенты, не являющиеся результатом измерения и известные совершенно точно, то число значащих цифр в этих коэффициентах не учитывают.
при извлечении корня и возведении в степень относительная погрешность и число значащих цифр сохраняются. Следовательно, 0,92 » 0,8 , а не 0,81;  » 17,3, но
» 17,3, но  » 2 !
» 2 !
при логарифмировании и потенцировании в мантиссе должно быть оставлено столько значащих цифр, сколько их имеется в логарифмируемом числе, и наоборот;
при многоступенчатых расчетах промежуточные результаты рекомендуется записывать с лишними значащими цифрами. До нужной степени округляют лишь окончательный результат. Перечисленные выше рекомендации относятся не только к результатам анализа, но и к любым расчетам, включающим результаты измерений.
Расчет доверительных интервалов. Результат анализа желательно выражать в виде доверительного интервала.
Доверительным интервалом называют интервал значений х, в котором в отсутствие систематических ошибок с заданной вероятностьюP находится неизвестное истинное содержание определяемого компонента.
Обычно доверительные интервалы рассчитывают для Р = 0,95. Иногда используют значения доверительной вероятности P = 0,90 или Р = 0,99, а для наиболее ответственных анализов можно даже взять Р = 0,999. Последнее означает, что вероятность нахождения истинного значения (m) измеряемой величины вне границ интервала (так называемый уровень значимости) не превысит 0,001, т. е. будет менее одного шанса из тысячи. При прочих равных условиях ширина доверительного интервала должна быть тем больше, чем больше желаемая вероятность P.
Если значение s для данной методики анализа известно, границы доверительного интервала рассчитать довольно просто. Можно найти эти границы, даже исходя из единичного результата анализа. В этом случае пользуются формулой:
(x – us) < m < (x + us). (2.9)
Коэффициент u зависит от выбранной доверительной вероятности (P). Его находят с использованием таблицы функций Лапласа. Значениям Р, равным 0,90; 0,95; 0,99 и 0,999, в этой таблице соответствуют значения u, равные 1,65; 1,96; 2,58; 3,29.
Лучше рассчитывать границы доверительного интервала, исходя из среднего результата, полученного по выборке из n вариант. При n > 1 применима формула:
( 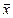 – us /
– us /  ) < m < (
) < m < ( 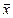 + us /
+ us /  ). (2.10)
). (2.10)
Величину us /  (или us, если n = 1) называют полушириной доверительного интервала. Для оценки истинного значения измеряемой величины часто пользуются двухсигмовым интервалом (x ± 2s), в такой интервал неизвестное значение m попадает с вероятностью, чуть большей 95 %. Если доверительный интервал получается слишком широким, следует увеличить в n раз число параллельных проб или повторных измерений, в этом случае ширина интервала сократится в
(или us, если n = 1) называют полушириной доверительного интервала. Для оценки истинного значения измеряемой величины часто пользуются двухсигмовым интервалом (x ± 2s), в такой интервал неизвестное значение m попадает с вероятностью, чуть большей 95 %. Если доверительный интервал получается слишком широким, следует увеличить в n раз число параллельных проб или повторных измерений, в этом случае ширина интервала сократится в  раз. Можно даже оценить, сколько раз надо повторять анализ, чтобы получить требуемую полуширину доверительного интервала (DX).
раз. Можно даже оценить, сколько раз надо повторять анализ, чтобы получить требуемую полуширину доверительного интервала (DX).
Гораздо сложнее достоверно оценить границы доверительного интервала при неизвестной величине s. Эта задача встает перед аналитиками очень часто: в их распоряжении оказывается лишь небольшая выборка экспериментальных данных (результатов повторных измерений или результатов анализа параллельных проб), и нужно оценить границы, в которых с заданной вероятностью находится неизвестное истинное содержание компонента. Задача решается по-разному, смотря по тому, каково распределение вариант, получаемых с помощью данной методики измерений. Для нормально-распределенных вариант используется способ, предложенный в начале ХХ века английским математиком В. Госсетом (Стьюдентом). Он доказал, что с надежностью Р можно считать, что
( 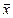 – t s /
– t s /  ) < m < (
) < m < ( 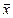 + t s /
+ t s /  ),(2.11)
),(2.11)
где t – коэффициент, зависящий от P и n. При прочих равных условиях величина t снижается по мере роста n и возрастает по мере роста P. Значения t (коэффициентов Стьюдента) приведены в виде таблиц во всех статистических справочниках. При пользовании ими следует учитывать, что вместо P в них часто указывают значения уровней значимости (a), дополняющие P до единицы, а вместо n указывают число степеней свободы df . При расчете доверительных интервалов df = n – 1.
Чтобы обеспечить более высокую вероятность попадания неизвестного истинного значения измеряемой величины в границы доверительного интервала, придется расширять этот интервал. Той же цели можно добиться, увеличивая число повторных измерений, либо переходя к другой методике, дающей лучшую сходимость (меньшее значение s).
Пример 2.5. Получена выборка из пяти вариант 17, 21, 18, 20, 19. Здесь  = 19; s = 1,58. По таблицам Стьюдента находим: t = 2,78 (P = 0,95, n = 5). Отсюда Δх = 1,97, а округляя Δx в большую сторону до одной значащей цифры (при расчете доверительных интервалов обычно поступают именно так), можно считать, что Δх » 2. Тогда истинное значение измеряемой величины с 95 %-ной надежностью должно попасть в доверительный интервал 19 ± 2, т. е. от 17 до 21.
= 19; s = 1,58. По таблицам Стьюдента находим: t = 2,78 (P = 0,95, n = 5). Отсюда Δх = 1,97, а округляя Δx в большую сторону до одной значащей цифры (при расчете доверительных интервалов обычно поступают именно так), можно считать, что Δх » 2. Тогда истинное значение измеряемой величины с 95 %-ной надежностью должно попасть в доверительный интервал 19 ± 2, т. е. от 17 до 21.
Необходимо помнить, что формулы Стьюдента справедливы только при одновременном выполнении трех условий: а) методика измерений не дает систематических погрешностей; б) результаты измерений по данной методике подчиняются нормальному распределению, независимы друг от друга и равноточны; в) отсутствуют дрейф и грубые промахи.
Сопоставление результатов анализа.Статистическое сравнение результатов анализа позволяет химику делать обоснованные выводы. Аналитикам требуется оценивать степень различия результатов анализа, полученных для одного и того же объекта по разным методикам. А другие специалисты таким же образом сравнивают результаты анализа, полученные по одной и той же методике для нескольких однотипных объектов. Выявленные различия могут оказаться статистически достоверными, тогда они будут воспроизводиться при повторении анализов. Если же различия статистически недостоверны, их можно объяснить не действительными отличиями сравниваемых методик или объектов анализа, а случайными факторами и малым объемом сопоставляемых выборок.
Результаты анализов обычно сравнивают по воспроизводимости и по среднему значению. Для этого вначале надо выполнить несколько (не менее двух) серий однотипных анализов и записать полученные выборки. Варианты сравниваемых выборок должны быть однотипными по своей природе, иметь одинаковую размерность и близкую величину. Объем выборок может различаться. Необходимо заранее проверить характер распределения вариант, отбраковать грубые промахи и убедиться в отсутствии дрейфа. Сопоставление выборок по воспроизводимости должно предшествовать сравнению средних
Сравнение двух выборок по воспроизводимости обычно ведут с помощью критерия Фишера. Несколько выборок сопоставляют более сложными способами, пользуясь критериями Бартлета, Кохрена и др. Если хотят использовать критерий Фишера, находят дисперсии обеих сопоставляемых выборок и делят большую на меньшую, независимо от объема той и другой. Полученное значение F =  сопоставляют с табличным значением критерия Фишера для некоторого значения доверительной вероятности (например, для P = 0,95) с учетом числа вариант в той и другой выборке. При F > Fтабл делают вывод о достоверном различии выборок по воспроизводимости измерений.
сопоставляют с табличным значением критерия Фишера для некоторого значения доверительной вероятности (например, для P = 0,95) с учетом числа вариант в той и другой выборке. При F > Fтабл делают вывод о достоверном различии выборок по воспроизводимости измерений.
Сравнение средних значений двух выборок проводят по критерию Стьюдента. Такое сопоставление возможно, если: а) в обеих выборках отсутствуют грубые промахи; б) измеряемая величина имеет нормальное распределение; в) дисперсии обеих выборок близки между собой. Для сравнения средних вначале вычисляют t по формуле:
 , (2.12)
, (2.12)
где в числителе стоят средние арифметические первой и второй выборок, а в знаменателе – обобщенное стандартное отклонение. Последнюю величину считают по-разному:
sd =  при n1 = n2 = n, (2.13)
при n1 = n2 = n, (2.13)
sd »  при n1 » n2. (2.14)
при n1 » n2. (2.14)
Величину t сравнивают с табличным значением для выбранной доверительной вероятности, при этом учитывают число вариант в каждой выборке. Различие средних достоверно, если найденное значение t больше, чем tтабл . Если t меньше, чем tтабл , то различие средних считается статистически недоказанным. Однако в этом случае не следует утверждать, что результаты анализа, представленные данными двух выборок, достоверно совпадают.
Пример 2.6.Содержание вредного вещества в сточной воде до очистки определяли по трем параллельным пробам. Получили следующие результаты (в мг/л): 129, 117 и 136. Отобрали также три пробы очищенной сточной воды и проанализировали по той же методике. Результаты: 98, 111 и 107 мг/л. Достоверно ли уменьшение среднего содержания примеси в результате очистки сточной воды или его можно объяснить случайными погрешностями анализа?
Решение. Прежде всего находим  = 127,
= 127,  = 105. Уменьшение среднего результата невелико и действительно может быть следствием случайных ошибок анализа, поэтому необходима статистическая проверка. Критерий Фишера для P = 0,95 и соответствующего числа вариант равен 19,2. Дисперсии:
= 105. Уменьшение среднего результата невелико и действительно может быть следствием случайных ошибок анализа, поэтому необходима статистическая проверка. Критерий Фишера для P = 0,95 и соответствующего числа вариант равен 19,2. Дисперсии:  = 92,
= 92,  = 44. Отношение дисперсий
= 44. Отношение дисперсий  = 2,08, оно намного меньше, чем Fтабл. Таким образом, воспроизводимость анализов до и после очистки можно считать примерно одинаковой. Это позволяет сравнивать по способу Стьюдента средние содержания примеси до и после очистки воды. Табличное значение t для P = 0,95 и 4 степеней свободы равно 2,78. По формуле (2.13) находим: sd = 6,8. По формуле (2.12) tэксп = (127 – 105) / 6,8 = 3,26, что больше tтабл. Следовательно, различие средних статистически значимо, его нельзя объяснить случайными погрешностями анализа. Эффект очистки невелик, но достоверен (на уровне P = 0,95).
= 2,08, оно намного меньше, чем Fтабл. Таким образом, воспроизводимость анализов до и после очистки можно считать примерно одинаковой. Это позволяет сравнивать по способу Стьюдента средние содержания примеси до и после очистки воды. Табличное значение t для P = 0,95 и 4 степеней свободы равно 2,78. По формуле (2.13) находим: sd = 6,8. По формуле (2.12) tэксп = (127 – 105) / 6,8 = 3,26, что больше tтабл. Следовательно, различие средних статистически значимо, его нельзя объяснить случайными погрешностями анализа. Эффект очистки невелик, но достоверен (на уровне P = 0,95).
Рассмотренный выше алгоритм используют и при выявлении дрейфа. В этом случае всю совокупность результатов (в порядке их получения) делят на две части. Затем оценивают различие средних значений обеих групп. Если они достоверно различаются, дрейф считают статистически доказанным. Однако этот способ применим не всегда, существуют и другие способы проверки. Статистические алгоритмы позволяют сравнивать результаты анализа не только друг с другом, но и с некоторыми нормативами. Этот прием широко применяется в аналитическом контроле производства.
2.6. Априорная оценка точности анализа
и пути ее повышения*
Точность любой методики анализа можно оценить двумя разными методами, хорошо дополняющими друг друга.
1. Можно оценить погрешности всех исходных данных (элементарные погрешности), а затем сложить их по специальным правилам. Способ применим для любых косвенных измерений, он позволяет еще до проведения анализа (заранее, априорно) быстро оценить общую погрешность будущего анализа. Однако обычно ее реальная величина оказывается выше ранее сделанных прогнозов. Это связано с появлением дополнительных систематических погрешностей, связанных с «химическими» факторами (неверно выбранным индикатором, неполным переводом вещества в осадок, наложением сигналов разных компонентов пробы и т. п.). Впрочем, дополнительные погрешности можно заранее оценить, а затем исключить.
2. Можно математически обработать результаты множества анализов, уже проведенных по исследуемой методике. Результаты сопоставляются с данными, относящимися к некоторым эталонам или стандартной методике. Соответствующие анализы и расчеты проводятся по строго определенным правилам, в рамках процедуры, называемой метрологической аттестацией методики. Такой способ длителен и трудоемок, но дает гораздо более надежные результаты, чем априорные оценки.
Оценка элементарных погрешностей. Часто в описании методик измерений (взвешивания, измерения объема и т. п.) величины соответствующих элементарных погрешностей (далее – D) не указаны. Тогда для оценки D сравнивают результат измерения с другим, полученным с помощью иного прибора или по иной методике, для которых погрешность измерений пренебрежимо мала. Расхождение результатов, полученных по проверяемой и по эталонной методикам, считают равным искомой величине D. Если же эталонных способов измерения в нашем распоряжении нет, можно приблизительно оценить D с помощью ряда простых приемов.
· Самый простой и распространенный способ – по цене деления измерительного прибора. Так, желая отмерить 250 мл раствора с помощью цилиндра, у которого деления нанесены через 10 мл, можно ошибиться на 10 мл. Это значение и берут в качестве оценки элементарной погрешности[2]. Данный способ не учитывает ни воспроизводимости измерений, ни систематических ошибок, т. е. дает заниженную оценку D.
· Можно вычислить D, если измерить по той же методике или с помощью того же прибора другой образец, однотипный исследуемому, но c точно известным значением m. Абсолютные погрешности измерений для обоих образцов считают одинаковыми. Этот способ оценки также не учитывает воспроизводимость измерений.
· Проводят несколько повторных измерений соответствующей величины для одного и того же объекта и оценивают расхождения полученных результатов. Так, если на одних и тех же весах одна и та же масса оказалась при повторных взвешиваниях 0,6547 г; 0,6608 г; 0,6531 г; 0,6472 г, то с учетом разброса результатов следует считать, что абсолютная погрешность этих весов имеет величину порядка 0,01 г. Этот способ оценки также дает заниженное значение D, не включающее систематическую составляющую общей погрешности. Не исключено, что при использования подходящего эталона абсолютная погрешность весов оказалась бы большей, например 0,10 г.
Правила сложения погрешностей.Чтобы оценить возможную погрешность косвенных измерений, надо складывать погрешности всех исходных данных (элементарные погрешности) по специальным правилам. При этом следует учитывать как характер элементарных погрешностей (случайные или систематические, независимые или взаимосвязанные), так и то, какие именно математические действия производятся над исходными данными при расчете результата анализа. Пусть y – результат анализа (или другого косвенного измерения), рассчитываемый на основе нескольких x – результатов прямых измерений, отягощенных погрешностями. Допустим, что известны только максимально возможные значения каждой из элементарных погрешностей (по абсолютной величине). Знаки каждой погрешности не учитывают. Допустим также, что при получении каждого x основную роль играют систематические погрешности (эта ситуация весьма типична). В таких случаях результирующую погрешность (Dy) рассчитывают по формулам:
при y = x1 + x2 или при y = x1 – x2
½Dy½ = ½D x1½ + ½ D x2 ½, (2.15)
при y = x1 x2 или при y = x1 / x2
½Dy / y½ = ½D x1 / x1½ + ½D x2 / x2½. (2.16)
Как видно из формулы (2.15), при оценке точности сумм и разностей суммируют модули абсолютных погрешностей всех слагаемых. Как видно из (2.16), при оценке точности произведений или частных суммируют модули относительных погрешностей сомножителей.
Если погрешности измерения разных x в основном носят случайный характер, то при y = x1 x2 или y = x1 / x2следует заранее оценить относительное стандартное отклонение каждого аргумента, а затем использовать формулу:
(sy / y)2 = (sx1/ x1)2 + (sx2/ x2)2. (2.17)
Пример 2.7.Погрешность аналитических весов Dg по модулю не превышает 0,001 г, масса тары с навеской (m) – 10,192 г, а масса пустой тары (m0) – 10,002 г. Определить абсолютную (Dm) и относительную (Dm, %) погрешность определения массы навески (mн).
Решение. Используем формулу (2.15), это приводит к Dm = 2 Dg = 0,002 г. Масса навески равна 0,190 г. Относительная погрешность взятия навески «по разности»: 0,002 г · 100 % / 0,190 г » 1 %. Заметим, что массу навески мы определили с довольно большой относительной погрешностью, тогда как единичное взвешивание тары давало очень небольшую относительную погрешность (порядка 0,01 %)! Здесь проявляется общее правило: относительная погрешность разности двух близких величин гораздо больше относительной погрешности исходных измерений.
Пример 2.8.В мерной колбе готовят по точной навеске раствор некоторого вещества. Концентрацию (С) рассчитывают по результатам прямых измерений массы реактива (m), объема колбы (V) и содержания (m) основного вещества в реактиве. Это содержание известно с точностью до 1 % и равно 99 %. Навеска реактива массой 5,000 г взята на весах, дающих погрешность порядка 0,001 г. Объем мерной колбы на 50 мл известен с точностью до 0,1 мл. Оценить относительную погрешность концентрации полученного раствора.
Решение. Концентрацию раствора рассчитываем по формуле С = mm / V, которая приводит к значению С = 0,100 г/мл. Так как в ходе расчета проводили действия умножения и деления, сложение элементарных погрешностей требует применения формулы (2.16). Прогнозируемая относительная погрешность концентрации равна:
DC /C = Dm /m + Dm/m + DV/V = (1/99) + (0,001/5) + (0,1/50) »
» 0,01 + 0,0002 + 0,002 » 0,012, т. е. 1,2 %.
Сопоставление слагаемых по величине показывает, что основную роль в данном случае играет неопределенность состава реактива, гораздо меньшее значение имеет неточность объема мерной колбы, а влиянием погрешности взвешивания можно пренебречь. Так поступают, когда одно слагаемое на порядок (в 10 и более раз) меньше других.
В случаях, не требующих высокой точности расчетов, можно считать, что точность конечного результата анализа (y) определяется лишь одним – наименее точным – слагаемым или сомножителем. В этом случае также следует сопоставлять либо абсолютные, либо относительные погрешности всех исходных данных. А именно: при сложении и вычитании наименее точным слагаемым считают то, у которого была самая большая абсолютная погрешность, тогда можно считать, что Dy » Dx. При умножении или делении наименее точным сомножителем считают тот, у которого самая большая относительная погрешность. В этом случае Dy/y » Dx/x . Если же y получают, умножая результат прямого измерения x на постоянный, точно известный коэффициент К, не являющийся результатом измерения, относительная погрешность y равна относительной погрешности x и не зависит от К.
Учет дополнительных погрешностей. Допустим, железо в руде определяют титриметрическим методом. Вначале отбирают некоторую пробу руды и точно измеряют ее массу (m, г), взвешивая пробу на аналитических весах. Затем пробу растворяют в кислоте, переводят соединения железа в ионы Fe2+. К полученному раствору постепенно прибавляют из бюретки раствор KMnO4 с точно известной концентрацией (С), прекращая этот процесс (титрование) при появлении розовой окраски, свидетельствующей о достижении точки эквивалентности. Объем затраченного раствора KMnO4 (титранта) точно измеряют (V, мл). Наконец, подставляют V, C и m в соответствующие расчетные формулы (см. раздел 5.2) и вычисляют массовую долю железа в руде (w), основываясь на известном уравнении реакции между Fe2+ и KMnO4. Затем суммируют погрешности измерения V, C и m по формуле (2.16), аналогично примеру 9.
Дополнительные погрешности анализа по изложенной методике могли быть связаны с неоднородностью состава руды, погрешностями пробоотбора, неполным переводом железа в ионы Fe2+, неверно установленным моментом окончания титрования и т. п. В пробе могли присутствовать другие вещества, которые реагировали с титрантом (чтобы проверить это предположение, потребовалось бы провести качественный анализ руды).
Некоторые дополнительные погрешности можно исключить, изменив методику анализа. Другие можно оценить расчетным путем, а затем исключить их, введя соответствующие поправки в результат анализа. Можно, в частности, учесть неполное осаждение определяемого вещества («потери при осаждении»), неточный подбор индикатора («индикаторные погрешности»), влияние примесей в реактивах («холостой опыт») и т. п. Так, если основным источником погрешности будет неполное осаждение Fe(OH)3 из-за проведения осаждения в слишком кислой среде или в присутствии веществ, связывающих Fe3+ в растворимые комплексные соединения, следует ожидать получения заниженных результатов анализа. Можно даже рассчитать, какова будет ошибка анализа, если проводить осаждение при том или другом значении рН. Вместе с тем, если в пробе железной руды, которую анализируют гравиметрическим методом, имеется примесь алюминия или титана, то гидроксиды этих элементов будут осаждаться вместе с гидроксидом железа. После прокаливания осадка его масса окажется больше массы оксида железа, результат определения железа будет завышенным. Тот же эффект дадут примеси железа в растворителях и химических реактивах, используемых в ходе анализа. Такие погрешности можно и нужно исключить, введя в результат анализа поправку на холостой опыт.
К сожалению, многие дополнительные погрешности (например, погрешности пробоотбора или персональные) заранее рассчитать и исключить очень трудно, их влияние оценивается только в ходе метрологической аттестации методики.
Метрологическая аттестация методики.Чтобы результаты количественного химического анализа были официально признаны («имели юридическую силу»), соответствующая методика анализа должна быть заранее согласована с органами Госстандарта, а для этого требуется провести ее метрологическую аттестацию. При этом можно использовать разные способы, в частности: анализ стандартных образцов, сравнение с более точной методикой, имеющей известные метрологические характеристики (стандартной методикой), а также метод добавок («введено – найдено»).
Принципы этих методов уже были охарактеризованы в разделе 2.4. Метрологическая аттестация требует определенного (весьма большого) объема экспериментальных данных и проводится по детально разработанным правилам, изложенным в нормативных документах Госстандарта. В качестве примера рассмотрим метод аттестации, основанный на применении стандартных образцов. В этом случае в лаборатории надо будет проанализировать не менее трех однотипных СО, близких по свойствам и составу, но существенно различных по содержанию определяемого компонента (Х). Содержание Х должно охватывать интервал концентраций, в котором планируется применять аттестуемую методику. Каждый СО анализируют не менее 10 раз, причем аналитический сигнал в каждом случае также измеряют несколько раз. Затем массив полученных данных обрабатывают с помощью специальных компьютерных программ, получая для каждого СО значения четырех статистических показателей. Это показатель сходимости sсх , показатель воспроизводимости sвоспр , показатель правильности Dс и показатель точности D. Все четыре показателя получают в тех же единицах, в которых представлены сами результаты. Два первых показателя характеризуют случайную составляющую общей погрешности (без учета и с учетом пробоотбора), третий – систематическую составляющую, четвертый – общую погрешность. Результаты аттестации позволяют понять, одинакова или различна погрешность анализа для разных содержаний определяемого компонента. Если эти погрешности достаточно малы, методика утверждается. Полученные в ходе аттестации показатели методики используют для расчета допустимых расхождений между результатами повторных анализов, а также для статистического контроля работы лаборатории.
Способы повышения точности анализа. Для достижения этой цели надо прежде всего понять, какая из составляющих общей погрешности – случайная или систематическая – в данном случае является основной. Именно ее и следует снижать в первую очередь, а затем перейти к устранению другой составляющей, меньшей по величине. Добиться высокой точности только путем повышения правильности или только путем повышения воспроизводимости анализа нельзя, надо использовать оба направления. Способы устранения случайных и систематических погрешностей различны. Разумеется, существуют и общие рекомендации, при выполнении которых уменьшаются обе погрешности (тщательное выполнение операций, описанных в методике; сокращение числа операций; использование приборов высокого качества, поверенных с помощью надежных эталонов; оптимизация условий проведения анализа и т. п.), но этого недостаточно, нужны специализированные способы, которые мы и рассмотрим по отдельности.
Снижение влияния случайных погрешностей достигается тремя основными способами: а) стабилизация условий проведения анализа; б) увеличение числа повторных измерений; в) повышение количества и размера проб исследуемого материала.
Стабилизация условий требует, чтобы все операции, выполняемые по ходу анализа, и особенно измерение аналитического сигнала проводились на одних и тех же приборах, с применением одной и той же мерной посуды, одних и тех же растворов и реагентов, одним и тем же человеком (этот подход иногда снижает не только случайную, но и систематическую погрешность). Даже порядок смешивания реактивов должен быть одним и тем же. Влияние колебаний рН при переходе от пробы к пробе можно устранить с помощью буферных растворов; влияние колебаний температуры – путем термостатирования исследуемых проб. Колебания напряжения в сети не скажутся на результатах анализа, если включать измерительный прибор через дополнительный стабилизатор. Список подобных рекомендаций можно продолжить, они специфичны для каждого метода анализа. Стабилизация условий достигается и путем автоматизации анализа – компьютерная программа, в отличие от человека-оператора, обеспечит для всех проб строго одинаковую методику проведения анализа.
Увеличение числа повторных измерений аналитического сигнала существенно снижает влияние случайных погрешностей. Современные автоматизированные аналитические приборы оснащают программным обеспечением, в котором предусматривается интегрирование и усреднение результатов многократных измерений. Например, потенциал электрода измеряется ежесекундно в течение 100 секунд, а затем по сохраненным в памяти прибора результатам повторных измерений автоматически вычисляется среднее арифметическое. Именно оно затем высвечивается на шкале прибора или используется для автоматического расчета концентрации.
Если основной вклад в общую дисперсию результатов анализа вносит не стадия измерения сигнала, а пробоотбор (так бывает нередко, особенно при анализе твердых и неоднородных материалов), то многократные измерения сигнала не помогут добиться высокой воспроизводимости результатов анализа в целом. Необходимо случайным образом отбирать большее число проб исследуемого материала, а затем усреднять полученные результаты. Так как неоднородность состава твердых материалов (например, горных пород или почвы) выражена преимущественно на микроуровне, следует брать пробы по возможности большего объема, а затем измельчать их, тщательно перемешивать и лишь затем уменьшать массу пробы.
Для профилактики систематических погрешностейособенно важны: выбор оптимальной методики, отделение и маскирование мешающих веществ, правильная настройка измерительных приборов, применение чистых реактивов, выбор наиболее подходящих эталонов, а также использование оптимальных способов расчета. Есть способы, специфичные для каждого метода анализа, они будут рассмотрены при изучении этих методов. Однако есть и общие способы, т. е. приемы, применимые для любых объектов и методов анализа. Одним из таких приемов является рандомизация. Этот терминозначает перевод систематической погрешности в разряд случайных, а затем ее уменьшение путем усреднения. Так, определение концентрации ионов кадмия можно проводить по нескольким разным методикам. Каждая из них дает некоторую систематическую погрешность, одни методики будут давать завышенное, другие – заниженное содержание кадмия. В серии результатов, полученных по разным методикам, погрешности приобретут случайный характер, будут компенсировать друг друга при усреднении. Среднее арифметическое окажется близким к истинному содержанию кадмия. Выигрыш будет тем большим, чем больше разных методик используют.
Контрольные вопросы
1. Что обозначают термины «количество вещества», «молярная концентрация», «мольная доля», «эквивалент»? Как связаны друг с другом молярная и нормальная концентрация одного и того же раствора? Как рассчитать молярную концентрацию раствора, если известна его процентная концентрация (массовая доля) и плотность?
2. Приведите 3–4 примера прямых измерений и столько же примеров косвенных измерений, которые можно провести в химической лаборатории. Какие средства измерений применяют при выполнении химических анализов?
3. Что такое «абсолютная погрешность»? Какую размерность может она иметь при проведении количественного химического анализа? С какой абсолютной погрешностью измеряют объем раствора, если пользуются: а) мерной колбой на 200,0 мл; б) пипеткой на 5,00 мл; в) бутылкой на 0,5 л ?
4. Что такое «относительная погрешность»? Оцените относительную погрешность, с которой взвешивают продукты (~ 0,5 кг) на торговых весах. Оцените относительную погрешность, с которой берут навески анализируемых веществ (~ 0,25 г) на аналитических весах. C какой относительной погрешностью нам известны атомные массы элементов, если судить по тому, как они записаны в таблице атомных масс?
5. Чем отличаются друг от друга систематическая и случайная погрешности измерений? Как оценить ту и другую? Когда можно считать одну из этих величин незначимой по сравнению с другой?
6. Почему результат химического анализа можно считать случайной величиной? Какие Вам известны теоретические распределения случайных величин? Чем отличается нормальное распределение случайных величин от других распределений?
7. Что такое воспроизводимость, сходимость, правильность, точность? Как Вы понимаете термины «выборка», «дисперсия», «варианта», «математическое ожидание»?
8. Как рассчитать стандартное отклонение некоторой выборки? Где в химическом анализе используется эта величина? Как связана воспроизводимость результатов анализа с концентрацией определяемого компонента? Что такое НГОС и как можно оценить ее величину?
9. Как можно проверить правильность результатов анализа? Какой из известных Вам способов проверки наиболее надежен?
10. Проверьте с помощью Q-теста, является ли результат единичного анализа – 37,6 % – грубым промахом, если при повторении анализа того же материала получены результаты 37,2 %, 36,9 %, 37,4 % 37,0 %. В каких случаях такая проверка может привести к ошибочным выводам?
11. Как правильно записать молярную концентрацию раствора NaCl, если навеску хлорида натрия массой 1,763 г растворили в мерной колбе на 25,0 мл и довели полученный раствор водой до метки?
12. Расставьте несколько величин в порядке возрастания точности их измерения: 0,002 м3; 920; 2100; 8100 г; 2,10 мл; 2100,0; 2,0·105 мин. Все величины записаны правильно, с учетом абсолютной погрешности соответствующих измерений.
13. Сформулируйте известные вам по школьному курсу математики правила округления. Сколько значащих цифр следует оставить в результате анализа, если его вычисляли путем умножения и деления результатов некоторых прямых измерений? Сформулируйте правила записи результатов косвенных измерений при сложении и вычитании.
14. Рассчитайте по Стьюденту доверительный интервал для влажности некоторого образца (в %), если три повторных результата анализа этого образца оказались равны 67, 64 и 66 %. Доверительную вероятность выберите самостоятельно. В каких случаях Ваш расчет привел бы к ошибочной оценке измеряемой величины?
15. В каких случаях после получения результата анализа можно внести численную поправку к этому результату? Как это можно сделать и почему этого лучше не делать?
16. Как сравнить между собой результаты анализа одного и того же материала по двум разным методикам, если анализ по каждой методике повторяли несколько раз?
[1] Метрологи считают, что систематической погрешностью можно пренебречь, если çq ç < 0,8 s. И, напротив, случайной погрешностью можно пренебречь, если çq ç > 8 s. В данном случае это условие выполняется.
[2] Поэтому в этом случае надо было записать отмеренный объем как 0,25 л или 2,5·102 мл, но не как «250 мл»!
