Растяжение и сжатие в конструкциях

В течение многих веков инженеры и архитекторы старались по возможности не нагружать материал растяжением. И это делалось не столько потому, что не было достаточно прочных на разрыв материалов (древесина, например, в этом отношении прекрасный материал), сколько из-за того, что очень трудно сделать достаточно прочное на разрыв соединение. (Большинство из нас интуитивно чувствует, что сжатая конструкция безопаснее растянутой; например, нам кажется, что кирпичная стена безопаснее подвесной канатной дороги.) Но когда все-таки приходилось соединять детали, работающие на растяжение, например на кораблях, места стыков всегда были наиболее уязвимым местом конструкции. Теперь мы научились делать надежные стыки с помощью болтов, заклепок, клея и сварки, и уже нет особых оснований не доверять таким конструкциям.

Однако в древности проблема соединений в сжатых конструкциях решалась намного проще, чем в растянутых. В самом простом случае это была укладка камней или кирпичей один к другому без применения раствора, и такое сооружение не рушилось. Эта работа требует навыка, но он не многим сложнее того, который приобретают дети, складывая картинки из кубиков. Однако с развитием архитектуры росла и высота стен, появилась необходимость надежнее связывать кирпичи и камни между собой. Иначе стены с грохотом превращались в груды камня: не связанные между собой камни расползались под весом верхней части кладки.

До наших дней сохранились великолепные образцы соединений в античных постройках. Правда, не ясно, насколько необходима была та тщательность, с которой выполнены большие каменные блоки этих сооружений. Вероятно, отчасти она определялась соображениями престижа. Но как бы то ни было, многие из древних построек поражают наше воображение.

Однако какой высокой и впечатляющей ни была бы стена, технически это не очень мудреная конструкция; ее создатель должен был думать лишь о напряжениях, действующих в одном направлении, по вертикали. Правда, перекрытия, двери, окна всегда вносят дополнительные трудности. А как только мы начинаем рисовать в своем воображении системы напряжений в двух и трех направлениях, перед нами открываются колоссальные возможности. Примером может служить арка. Самая простая арка (рис. 6) работает на сжатие одновременно в двух направлениях, хотя на первый взгляд это кажется невозможным. Кирпичной аркой можно без особых ухищрений перекрыть пролет длиной около 50 м (чаще встречаются пролеты в 25–50 м). Это намного больше того, чего удается добиться с помощью любого простого балочного перекрытия. Арки очень долговечны, и до наших дней в отличном состоянии сохранилось много древ неримских арок, с их помощью, например, перебрасывали водопроводы через овраги.

Рис. 6. Арка, представляющая собой конструкцию, работающую на сжатие в двух направлениях

Формирование представлений о сложном напряженном состоянии стимулировало громадный скачок в раз витии не только архитектуры, но и техники. Как только была принята концепция двумерной арки, а вслед за этим сделан следующий логический шаг - к трехмерному куполу, - архитектура стала творить чудеса. Центральная часть собора св. Софии, построенного в Константинополе около 530 года при императоре Юстиниане, представляет собой огромный купол, диаметр которого достигает 33 м. Для легкости он сложен из пемзы и покоится на громадных арках, которые в свою очередь опираются на вспомогательные полукупола (рис. 7). Раз меры свободного от каких-либо колонн пространства площадью более чем 60x30 и высотой около 80 м были, вероятно, непревзойденными вплоть до постройки современных вокзалов, крыши которых держатся на металлических стропилах.

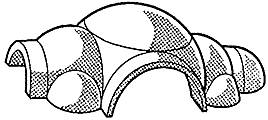
Рис. 7. Макет куполов собора св. Софии в Константинополе.

Формы византийских зданий, как правило, просты. Готические же архитекторы, давая волю своему воображению, создавали перекрытия, боковые приделы, витражи. И хоть это, надо думать, обходилось недешево, такие постройки, если они были сделаны со вкусом и знанием дела, могли служить образцами инженерного искусства и художественного мастерства. Что же касается каменной кладки, то она должна быть выполнена так, чтобы напряжения во всех точках конструкции были сжимающими: ведь кладка совсем не сопротивляется растяжению, под действием которого она разваливается по швам.

Готические архитекторы, пытаясь заставить конструкцию работать на сжатие, не прибегали к математике, и поэтому в трехмерные лабиринты соборных крыш чертом прокрадывалось растяжение. Так обрушилась башня одного из самых больших готических соборов - собора в Бове (1247), крыша его проваливалась дважды. Архитекторы знали лишь качественную сторону подобных катастроф и пытались предупредить их, подкрепляя конструкции частоколом контрфорсов (рис. 8).

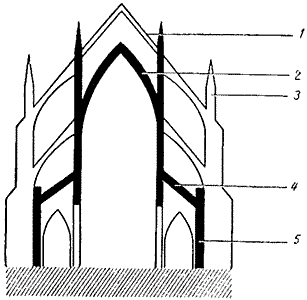Рис. 8. Типичная конструкция готического собора с контрфорсами 1 - деревянная крыша; 2 - арочный свод; 3 - контрфорс; 4 - деревянная крыша бокового придела; 5 - стена придела.

В соборе св. Софии эта задача решалась и рациональнее и успешнее: там вспомогательные купола давили на главный купол и создавали сжатие в опасной области. Однако иногда готические зодчие перебарщивали: создавая слишком большие боковые давления, они должны были ставить подпорки изнутри, чтобы предотвратить разрушение крыш. Эти подпорки чаще всего делались в виде перевернутых арок, подобных аркам собора в Уэлсе (Великобритания), который, как бы ни оценивали его в эстетическом плане, технически построен неграмотно (рис. 9). Не удивительно, что крыши церквей довольно часто рушились на головы коленопреклоненных прихожан.

Рис. 9. Собор в Уэльсе (Великобритания).

Каменная кладка остается целой благодаря силам тяжести, то есть при правильно спроектированной кладке вес камня создает безопасную сжимающую нагрузку во всех ее точках. А если этого веса не хватает, к зданию всегда можно добавить бельведеры или башни. Если же в конструкции появляются растянутые области, то, безусловно, растягивающие и сжимающие нагрузки (в том числе нагрузки от веса сооружения) должны быть уравновешены. Так, канаты подвесного моста (рис. 10) находятся в растянутом состоянии, а грунт под мостом оказывается сжатым. Растяжение в брезенте и растяжках палатки уравновешивается сжатием в центральной подпорке и на той земляной площадке, где установлена палатка. На плывущем корабле растяжение в парусах и оснастке вызывает сжатие мачт и рангоутов. В теле животных сжимающие нагрузки воспринимаются скелетом, в основном позвоночником; эти напряжения возникают не только под действием собственного веса, но и вследствие растяжения в мышцах и сухожилиях. Сокращая мышцу, я поднимаю руку, в это время мышца передает сжимающую силу кости, а кость легко выдерживает сжатие. Если нога попадает в условия, когда на нее действует изгиб - а изгиб включает растяжение, - нога может сломаться.

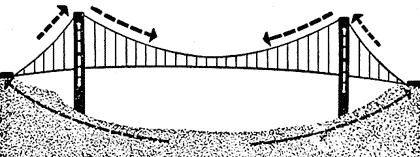
Рис. 10. Растяжение в тросах балансируется сжатием в грунте

Когда мы располагаем материалами, одинаково хорошо работающими и на сжатие и на растяжение, наши конструкции оказываются проще и безопаснее. Именно поэтому в строительстве удобны железобетон и стальные конструкции.
Инженерам повезло, в их распоряжении есть железо и сталь - ведь мы часто и не знаем, какого рода напряжения придется выдержать машине во время работы. Например, стенки парового котла работают на растяжение, но если по какой-то причине давление пара упадет ниже атмосферного, котел будет сжат разностью давлений, однако со стальным котлом ничего страшного не произойдет.

К довольно неожиданным эффектам, с которыми приходится бороться, могут привести сжимающие напряжения в корпусе подводной лодки. Когда лодка находится в надводном положении, она плавает, как любое другое судно, поскольку ее вес меньше веса воды, которая может быть вытеснена объемом лодки. Чтобы лодка погрузилась, балластные цистерны заполняют водой настолько, чтобы вес лодки был равен весу воды в ее объеме. Тогда "удельный вес" лодки будет равен удельному весу воды, и лодка не будет иметь запаса плавучести.

Теперь лодка может опускаться на глубину и маневрировать примерно так же, как это проделывает дирижабль в воздухе. Однако, погружаясь глубже, лодка испытывает все большее и большее давление воды, и сжимающие напряжения в ее корпусе растут. Поскольку давление внутри лодки остается примерно постоянным, корпус ее сжимается, уменьшается объем, а следовательно, уменьшается и выталкивающая сила. Если вес лодки вместе с балластом не изменяется, она стремится провалиться глубже, и при некоторых обстоятельствах этот процесс может стать опасным. На предельной для подводной лодки глубине погружения величина деформации сжатия может составить около 0,7%. Деформация происходит во всех трех направлениях, поэтому объем лодки может уменьшиться примерно на 2%. Так как сжимаемость воды очень невелика, то для лодки весом 1000 т это будет означать потерю выталкивающей силы примерно 20 т *. Если эту силу не компенсировать, частично опорожняя балластные цистерны от воды, подводная лодка будет опускаться все глубже и глубже, пока ее не раздавит давлением воды. В этом, между прочим, заключается одна из трудностей постройки подводной лодки из стеклопластиков, которые всем, пожалуй, хороши, кроме модуля упругости: он слишком мал.

* Общий вес балластной воды, необходимой для погружения такой лодки, будет около 100 т. Следовательно, упругая деформация корпуса потребует заметного изменения балласта.

Иногда думают, что затонувшие подводные лодки "висят" где-то поблизости от океанского дна. Это, конечно, нелепое представление: если корпус потерпевшей аварию лодки и не сомнет давлением воды, что случается чаще всего, то он будет непрерывно сжиматься, выталкивающая сила будет падать и лодка будет опускаться на дно все быстрее и быстрее.

Воздушные шары, пневматические шины и т. п. представляют особый случай конструкции, в которой растягивающие напряжения в оболочке уравновешены давлением наполняющего их газа или жидкости. Поэтому большие баржи-мешки и надувные лодки обычно очень легкие и эффективные конструкции. Изобретение крыш, поддерживаемых изнутри воздухом, заставляет пересмотреть прежние архитектурные традиции, в этих конструкциях все элементы работают на растяжение, лишь воздух внутри здания сжат.

Балки и изгиб

Итак, мы знаем теперь, что понять, как работает конструкция на растяжение и сжатие, довольно легко. Но вот как те же самые растяжение и сжатие позволяют балкам выдерживать нагрузки - это далеко не очевидно. А между тем разного рода балки (рис. 11) составляют львиную долю всех конструкций, с которыми мы повседневно сталкиваемся. Самая обычная половая доска - наглядный пример балки, и таких примеров можно привести огромное множество. Мы уже говорили, что задача этой самой доски заключается в том, чтобы давить на наши подошвы вверх с силой, в точности равной нашему весу. Естественно, эту роль пол должен играть постоянно, в том числе и тогда, когда мы стоим посреди комнаты, далеко от стены, которая в конечном счете будет воспринимать силу нашего веса. Но позвольте, как эта сила передается от стены на наши ноги, и обратно?

Рис. 11. Свободно опертая балка.

Ответ на этот вопрос дает так называемая теория балок, которую, пожалуй, можно назвать становым хребтом техники. Но, к сожалению, этот "хребет" представляет собой pons asinorum * для студентов технических вузов. Большинство из них механически заучивают формулы теории балок лишь для того, чтобы проскочить на экзаменах; понимать эти формулы они начинают гораздо позже, когда настает время мучаться над собственными проектами. Поэтому давайте пока оставим всю эту кухню интегрирования эпюр и попытаемся подступиться к существу проблемы.

* Мост для ослов (лат.). Так говорят о том, что, не являясь сложным само по себе, представляет тем не менее затруднение для начинающего. Источник выражения - "Геометрия" Евклида (III век до н.э.). - Прим. перев.

Начнем с того, что вспомним высказанную ранее мысль об отсутствии четкого различия между понятиями "материал" и "конструкция". Большие балки, например перекрытия железнодорожных мостов, подобно детскому конструктору, собираются из многих малых стержней. Эти стержни работают как на растяжение, так и на сжатие. Способ передачи нагрузки в такой решетчатой балке, или ферме, по существу не отличается от того, как передается нагрузка в сплошной балке, даже такой, как половая доска. В решетчатой балке вся нагрузка передается только путем сжатия и растяжения стержней. В сплошной балке такой решетки нет, но мы можем представить себе ее как бы прошивающей всю балку.

Для определенности начнем анализ с консольной балки, то есть с балки, один конец которой встроен в стену или жестко закреплен каким-либо другим способом на любом основании (на языке инженеров это называется "заделка"): к другому концу консоли приложена нагрузка. Такую консоль рисовал еще Галилей (рис. 12); правда, он неверно рассчитал прочность своей консоли, что, впрочем, ему простительно. Мы же построим нашу консоль только из стержней и натянутых струн.

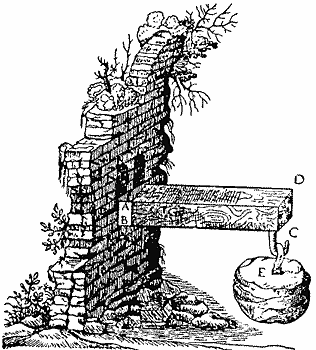Рис. 12. Рисунок Галилея, иллюстрирующий испытания консольной балки.

Рассмотрим простую конструкцию типа крана, изображенную на рис. 13, а. Сжатый стержень 2 опирается на стену и поддерживается струной 1, таким образом он может воспринимать внешнюю нагрузку (назовем ее W). Очевидно, сила, противодействующая нагрузке W, возникает вследствие сжатия наклонного стержня 2. Натяжение горизонтальной струны 1 лишь предохраняет сжатый стержень 2 от поворота и падения.

С таким же успехом мы можем воспользоваться другой треугольной конструкцией (рис. 13, б), в которой сжатый стержень 4 занимает горизонтальное положение и удерживается от падения наклонной растянутой струной 3. В этом случае сила, удерживающая вес W, обеспечивается струной, а горизонтальный сжатый стержень необходим лишь для того, чтобы струна не прижималась к стене.

Обе эти конструкции одинаково хороши, и мы можем объединить их в одну, способную выдержать вес 2W, как показано на рис. 13, в. Ясно, что нагрузка 2W непосредственно воспринимается наклонными элементами 2 и 3, один из которых сжат, а другой растянут. Горизонтальные элементы 1 и 4 воздействуют на стену, один из них давит, другой - тянет, вместе они обеспечивают целостность конструкции, но не поддерживают вес груза непосредственно.

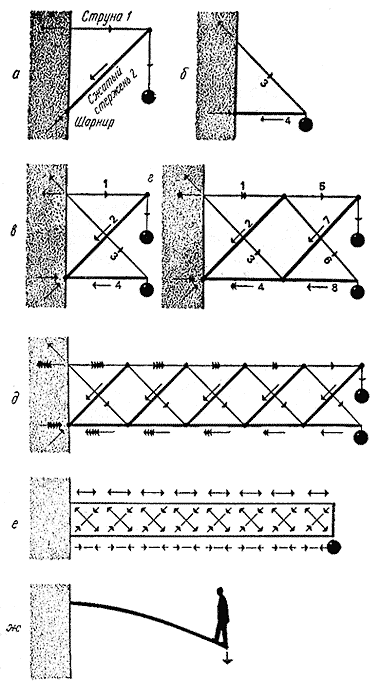Рис. 13. Сопоставление напряженного состояния в сплошной балке и решетчатой ферме.

Пристроив к полученной конструкции еще одну, точно такую же, мы получим новую ферму, показанную на рис. 13, г. В этом случае тот же самый груз 2W поддерживается сжатыми и растянутыми наклонными элементами 2, 3, 6 и 7, в то время как элементы 1, 5, 4 и 8 сжаты и растянуты в горизонтальном направлении и, хотя они не поддерживают внешнюю нагрузку непосредственно, благодаря им ферма не рушится. Получается, что каждый элемент выполняет свою функцию и, если хотя бы один стержень или одна струна выйдет из строя, катастрофа неизбежна: каждый элемент по-своему важен.

Теперь посмотрим, как передается в нашей ферме нагрузка от элемента к элементу. Правая ячейка на рис. 13, г работает точно так же, как единственная ячейка на рис. 13, в. Однако в левой (внутренней) ячейке на рис. 13, г дело обстоит иначе. Растягивающее напряжение в струне 1 вдвое больше напряжения в струне 5, а сжатие в стержне 4 в два раза превышает сжатие в стержне 8. Это происходит потому, что диагональные элементы (назовем их "сдвиговыми") добавляют нагрузку на элементы, расположенные по направлению к месту заделки консоли. Однако во всех сдвиговых элементах независимо от длины фермы нагрузка одинакова.

Мы можем продолжать нашу ферму, пристраивая к ней все новые и новые ячейки, как это показано на рис. 13, д. Внимательно посмотрев на рисунок, мы поймем, что и здесь напряжения во всех диагональных элементах одинаковы. С другой стороны, напряжения сжатия и растяжения в нижних и верхних горизонтальных элементах от ячейки к ячейке возрастают (если двигаться от точки приложения нагрузки к месту заделки консоли). Нетрудно доказать, что это возрастание напряжения пропорционально номеру элемента (опять-таки считая от точки нагружения). Именно поэтому консоль всегда ломается в месте заделки, у стены, где возникают наибольшие напряжения, если, конечно, заранее не позаботиться о ее прочности и не подобрать все стержни соответственно действующей нагрузке. Если такой подбор сделан строго пропорционально нагрузке, то ферма становится равнопрочной, то есть может сломаться в любом месте, а это идеальный случай, составляющий цель многих расчетов на прочность. Совершенно ясно, почему мы хотим, чтобы материал был напряжен во всех точках одинаково; в этом случае материал используется с максимальной эффективностью, а конструкция имеет минимальный вес.

Если теперь мы преобразуем нашу ферму или балочку, построенную из детского конструктора, в сплошную балку, то получим систему напряжений, изображенную на рис. 13, е. В средней по высоте части балки под углом 45° к оси действуют главным образом сдвиговые напряжения, неизменные по длине балки. Материал верхней и нижней частей балки нагружен в основном растяжением и сжатием. Горизонтальные напряжения растяжения-сжатия быстро возрастают по длине балки и в наиболее опасном сечении становятся намного больше сдвиговых напряжений. Именно эти напряжения обычно повинны в разрушениях балочных конструкций и тяжелых несчастных случаях, которые за ними следуют. Вот почему вычисления, связанные с расчетом напряжений, - это совсем не сухие академические упражнения, интересные только специалистам, они прямо связаны с безопасностью и благополучием большинства из нас.

Если вся эта охота за напряжениями покажется читателю несколько непонятной, лучше всего сделать модель из детского конструктора или из соломинок для коктейлей, скрепляя их обыкновенными булавками. Поразмыслив над такой моделью, вы поймете, что представляет собой консоль вообще и как она выдерживает нагрузку. Конечно, сколь сложным бы ни было напряженное состояние, мы должны отдавать себе отчет в том, что любое напряжение связано с деформацией, поэтому консоль неизбежно должна в большей или меньшей степени прогибаться под нагрузкой (рис. 13, ж).

Консоли широко распространены в технике, но еще чаще используются обычные балки, вроде тех, которые принято называть "свободно опертыми" (рис. 14). Примером такой балки может служить доска, переброшенная через канаву или ручей. Как же такая балка соотносится с консольной? Наглядный ответ на этот вопрос дает рис. 14. Дело в том, что свободно опертую балку можно рассматривать как две консоли, жестко связанные друг с другом в местах заделки и перевернутые на 180°. В то время как наибольшее напряжение в консоли возникает в месте ее заделки, в нашей новой балке оно будет в центре. Поэтому такие балки обычно ломаются пополам.

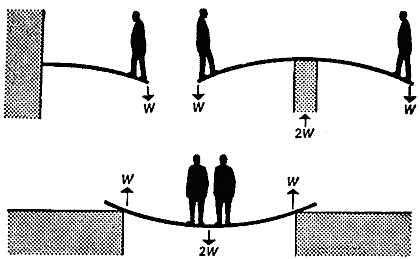
Рис. 14. Свободно опертая балка, которую можно рассматривать как две консоли, сложенные вместе у заделок и перевернутые на 180 градусов.

Теперь нам понятно, почему мы не проваливаемся сквозь пол: напряжения в досках передаются зигзагами, под углом 45° к поверхности, от наших подошв до стены, обеспечивая в результате силу, направленную вверх, которая нас и держит. Вместе с этими сдвиговыми напряжениями в доске вблизи верхней и нижней ее поверхностей возникают напряжения растяжения - сжатия, направленные горизонтально. Если по какой-либо причине эти напряжения окажутся слишком большими (на доску наступил чересчур грузный человек или сама доска слишком тонка), мы сначала обнаружим тревожный прогиб доски, а уж затем раздастся треск.

Каждый может поставить простой эксперимент, который покажет, что напряжения и перемещения, вызванные изгибом, намного опаснее тех - при прочих равных условиях, - которые вызваны растяжением или сжатием. Действительно, возьмите какую-нибудь деревянную планку или стержень и попробуйте разорвать ее руками. Как правило, этого вам сделать не удастся, как не удастся и заметить на глаз удлинение вашего образца. Теперь начинайте гнуть стержень, и вы тут же заметите вполне ощутимый прогиб, а возможно, и без особого труда сломаете образец. Этим объясняется то обстоятельство, что балки почти всегда требуют тщательной расчетной проверки прочности и жесткости. Такой расчет может сделать каждый, кто знаком с элементарной алгеброй, по стандартным формулам, приведенным в конце книги.

Мы уже говорили, что разобраться в теории изгиба балок не так-то просто, но, откровенно говоря, особого напряжения интеллекта для этого не требуется, да и многое в технике станет гораздо яснее. По правде сказать, проектируя даже весьма внушительные конструкции, инженеры зачастую пользуются почти элементарной теорией изгиба. Далее мы увидим, что такая практика иногда может быть опасной, поскольку элементарная теория, будучи чрезвычайно полезной, все же не дает нам достаточно полного представления о прочности сложных конструкций. Тем не менее она очень широко используется для прикидочных оценок прочности любых конструкции, от коленчатого вала до морских судов.

Большие балки начали использовать в технике по существу не столь давно, немногим более столетия назад. Английскому инженеру Телфорду (1757–1834) дали много лестных прозвищ за искусство строить мосты, он построил их, вероятно, больше, чем кто-либо другой. Обычно Телфорд применял каменные или чугунные арки, работающие на сжатие, а для больших пролетов первым стал строить подвесные мосты, используя железные цепи (мост через пролив Менай - 1819 год). Вряд ли Телфорд когда-либо применял большие балки, отчасти из-за отсутствия подходящего материала - кованых железных плит, а отчасти оттого, что не было надежной теории балок. Между прочим, об уровне расчетов на прочность в то время можно судить по тому, что форма линии цепей для упомянутого моста определялась не расчетным путем, а на специально построенной большой модели моста, переброшенной через овраг.

Лет тридцать спустя Роберт Стефенсон (1803–1859) уже имел в своем распоряжении листы котельной стали; кроме того, он верил своим расчетам. Ему принадлежит блестящая идея * изготовить из листов железа балку в виде полого короба и пустить внутри нее поезда. Так, в 1850 году был построен недалеко от телфордова моста железнодорожный мост через Менай. Каждая балка Стефенсона весила 1500 т, они были собраны на берегу, за тем спущены на плотах на воду, установлены на плаву поперек узкого бурлящего потока между опорами, после чего примитивные гидравлические домкраты за несколько приемов подняли всю конструкцию метров на тридцать к опорам. Хотя вся операция проводилась с полным пониманием дела, она не лишена была элементов риска; по тем временам это был выдающийся подвиг.

* В действительности эту честь он должен разделить со своим коллегой Вильямом Фэйрбэрном.

Несколько позже Стефенсона одолели сомнения, и было предложено укрепить мост, подвесив трубу на цепях, но это оказалось совершенно излишним. Оба моста по сей день стоят рядом - превосходные образцы использования растяжения и изгиба в технике. Подвесной мост Телфорда вначале был недостаточно жестким, штормовые ветры, гулявшие вдоль пролива, угрожающе раскачивали его. Рассказывают, как однажды зимней ночью лошади почтовой кареты не смогли удержаться на ногах, и во избежание неприятностей пришлось срочно пережигать постромки огнем фонаря. После этого случая мост был укреплен, и в таком виде он служит до сих пор. Недостаточная жесткость подвесных мостов делает их непригодными для железнодорожных целей: поезд может сойти с рельсов. Именно поэтому Стефенсон и Брюнель (1806–1859) разработали для больших пролетов балочные мосты. Но хотя трубчатый мост через Менай имеет великолепную жесткость и никогда не вызывал беспокойства, в настоящее время подобные мосты имеют решетчатую конструкцию. Такие мосты экономичнее как в постройке, так и в эксплуатации.

Корабль также представляет собой длинную закрытую с двух сторон трубу, которой назначено плавать. Отличие такой конструкции от стефенсонова моста по существу невелико. Корпус корабля порой не выдерживает веса двигателей, груза, топлива, которые он несет, и изгибается. Глядя на стоящее у причала судно трудно себе представить, что его можно разрушить неосторожной или неравномерной загрузкой трюмов и цистерн. Однако такие трагедии случались довольно часто и, судя по всему, не исключены и в будущем. В сухом доке корабль тщательнейшим образом устанавливается на специальные килевые подставки, чтобы корпус опирался на них равномерно, но в плавании такие равномерные опоры отсутствуют. Корабль может быть поднят двумя мощными волнами за нос и корму, а его середина окажется без опоры. Бывает и так, что самая мощная волна может оказаться под центральной частью корпуса.

Рис. 15. Корабль "Скенектеди". Трещина началась у острого угла люка на палубе и "побежала" до самого киля

Корабли становились все больше, длиннее, а инженеры стремились сделать их легче. В 1903 году Британское Адмиралтейство решило провести специальные испытания судов на прочность. С этой целью эскадренный миноносец "Волк" был заведен в сухой док. После откачки воды подпорки были оставлены сначала только посредине, а затем лишь по краям судна. При этом с помощью тензометров - приборов для измерения удлинений, а следовательно, и деформаций материала - измерялись напряжения в различных частях корпуса. Затем "Волк" вышел в открытое море для продолжения испытаний в плохую погоду. Легко себе представить экспериментаторов, в темных трюмах борющихся с морской болезнью и тогдашними не очень покладистыми тензометрами, - в официальном отчете состояние моря называлось "чрезвычайно бурным с сильным ветром". Капитан делал все, что было в его силах, чтобы этот поход был худшим для "Волка". Но как он ни старался, а напряжения в корпусе нигде не превышали 9 кг/мм², в то время как прочность сталей, используемых в кораблях, была примерно 40–45 кг/мм².

После этих двух испытаний кораблестроители решили, что стандартный метод расчета прочности судов по простой теории изгиба балок вполне их устраивает, поскольку он обеспечивает достаточно большой запас прочности. Порой никто не бывает так слеп, как эксперты.

Корабли продолжали время от времени ломаться по полам. Такое стряслось, например, со стометровым пароходом, груженным рудой, на одном из Великих озер в Америке во время шторма. Максимальное напряжение в таких условиях по расчетам должно было составлять не более одной трети от предела прочности материала судна.

Даже когда не случалось самого страшного, появлялись трещины вокруг люков и других отверстий в корпусе *. Безусловно, корень зла крылся именно в этих отверстиях. Трубчатый мост Стефенсона оказался исключительно надежным, потому что представлял собой сплошную оболочку, если не считать отверстий под заклепки. Конечно же, британские кораблестроители не могли не принять во внимание возможность увеличения напряжения пропорционально уменьшению площади поперечного сечения за счет всех этих отверстий. Однако профессор Инглис в своей знаменитой статье, написанной в 1913 году, показал, что такой подход не очень хорош **. Он ввел понятие "концентрации напряжений", которое, как мы увидим ниже (глава 4), имеет жизненно важное значение в расчетах прочности конструкций.

* В 1966 году почетный вице-президент Королевского общества кораблестроителей Дж. Муррей заявил: "С 1950 года лишь 26 судов разрушились в открытом море. Из большого числа судов, благополучно проплававших в море и затем обследованных в доках, примерно 20% имели трещины в главной корпусной ферме" ("Таймс" от 23 марта 1966 года). Несколько дней спустя пришло известие о двадцать седьмом судне, сломавшемся пополам в штормовую погоду на Тихом океане.

* Впервые задача о концентрации напряжений была решена русским ученым Г.В. Колосовым. - Прим. перев.

Что показал Инглис? Он нашел, что если мы, вырезав в пластинке отверстие, уменьшим сечение, скажем, на од ну треть, то напряжение на кромке отверстия не будет составлять 3/2 от первоначального, а может быть во много раз больше. Число, показывающее, во сколько раз местное напряжение превышает среднее значение напряжения - коэффициент концентрации напряжений, - зависит от формы отверстия, или надреза, и от свойств материала. Наихудшая ситуация возникает в случае острых над резов и хрупких материалов.

Этот вывод Инглиса, который он получил чисто математическим путем, был встречен с обычным пренебрежением тем удивительно непрактичным племенем людей, которые сами себя зовут почему-то "практиками". Произошло это в основном потому, что мягкая сталь менее других материалов чувствительна к концентрации напряжений, хотя и ни в коем случае не безразлична к ней.

Глава 2.