Метод валентных связей (МВС).
Метод валентных связей (МВС) иначе называют теорией локализованных электронных пар, поскольку в основе метода лежит предположение, что химическая связь между двумя атомами осуществляется с помощью одной или нескольких электронных пар, которые локализованы преимущественно между ними. В отличие от ММО, в котором простейшая химическая связь может быть как двух-, так и многоцентровой, в МВС она всегда двухэлектронная и обязательно двухцентровая. Число элементарных химических связей, которые способен образовывать атом или ион, равно его валентности. Так же, как и в ММО, в образовании химической связи принимают участие валентные электроны. Волновая функция, описывающая состояние электронов, образующих связь, называется локализованной орбиталью (ЛО).
Отметим, что электроны, описываемые ЛО, в соответствии с принципом Паули должны иметь противоположно направленные спины, то есть в МВС все спины спарены, и все молекулы должны быть диамагнитны. Следовательно, МВС принципиально не может объяснить магнитные свойства молекул.
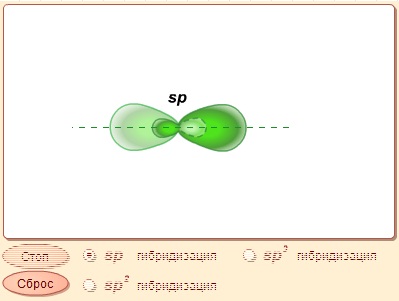
Тем не менее, принцип локализованных связей имеет ряд важных преимуществ, одно из которых – его чрезвычайная наглядность. МВС достаточно хорошо, например, предсказывает валентные возможности атомов и геометрию образующейся молекулы. Последнее обстоятельство связано с так называемой гибридизацией АО. Она была введена для объяснения того факта, что двухэлектронные двухцентровые химические связи, образованные за счет АО в разных энергетических состояниях, имеют одинаковую энергию. Так, Be*(2s11p1), B*(2s12p2), C*(2s12p3) образуют за счет s- и p-орбиталей соответственно две, три и четыре связи, а потому одна из них должна быть прочнее других. Однако опыт показывает, что в BeH2, BCl3, CH4 все связи равноценны. У BeH2 угол связи равен 180°, у BCl3 – 120°, а у CH4 – 109°28'.
| Модель 3.4. Гибридизация орбиталей. |
| В этой модели вы можете наблюдать процесс гибридизации атомных орбиталей. В случае, когда атом устанавливает с другим атомом химическую связь, форма атомных орбиталей не обязательно сохраняется. Особенно интересно поведение s- и p-орбиталей атомов p-элементов второго периода. Рассмотрим гибридизацию этих орбиталей на примере атома углерода. Образованию химической связи углерода должно предшествовать возбуждение одного 2s-электрона на вакантную 2p-орбиталь. Тогда все четыре орбитали становятся эквивалентными по заселенности их электронами, но остаются неэквивалентными по энергии. Гибридизация заключается в том, чтобы превратить разные по симметрии и энергии s- и p-орбитали в эквивалентные по энергии и симметрии, но отличающиеся при этом расположением в пространстве. При комбинации сферически симметричной 2s-орбитали и гантелеобразных 2p-орбиталей образуется две, три или четыре гибридные атомные орбитали в форме несимметричной гантели. Форма гибридной орбитали слабо зависит от того, образована такая орбиталь в результате гибридизации одной s- и одной p-орбитали (sp-гибридизация), одной s- и двух p-орбиталей (sp2-гибридизация) или одной s- и трех p-орбиталей (sp3-гибридизация). Зато расположение гибридных орбиталей друг относительно друга очень сильно зависит от вида гибридизации. sp-гибридизация: Вы увидите, что расположение двух образовавшихся гибридных орбиталей линейно. Это обусловливает линейную форму молекул, в которых такая гибридизация осуществляется (молекулы с тройной связью между атомами углерода, например, молекула ацителена. См. модель «Сигма- и пи-связи»). sp2-гибридизации: Получившиеся три гибридные орбитали расположены на плоскости и повернуты под углом 120°, что обусловливает плоскую структуру молекул с двойной связью, в которых осуществляется такая гибридизация. Пример – молекула этилена (cм. модель «Сигма- и пи-связи»). sp3-гибридизации: Вы увидите, что получившиеся гибридные орбитали направлены к вершинам тетраэдра, центр которого совпадает с ядром атома углерода. Молекула метана имеет форму тетраэдра, в вершинах которого расположены атомы водорода, а в центре – атом углерода. |
Согласно представлению о гибридизации, химические связи образуются смешанными – гибридными орбиталями (ГО), которые представляют собой линейную комбинацию АО данного атома (s- и p-АО Be, B, C), обладают одинаковыми энергией и формой, определенной ориентацией в пространстве (симметрией). Так s- и p-орбитали дают две sp-ГО, расположенные под углом 180° друг относительно друга.
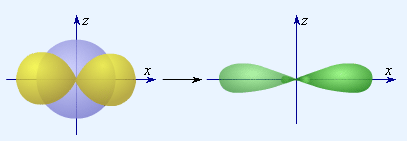 |
| Рисунок 3.16. s-орбиталь + p-орбиталь и две sp-ГО. |
В молекуле CH4 гибридные орбитали из четырех АО углерода (одной s и трех p), называются sp3-орбиталями, они полностью эквивалентны энергетически и пространственно направлены к вершинам тетраэдра.
Таким образом, когда один атом образует несколько связей, а его валентные электроны принадлежат разным орбиталям (s и p; s, p и d), для объяснения геометрии молекул в МВС необходимо привлекать теорию гибридизации атомных орбиталей. Основные положения теории следующие:
1. Введение гибридных орбиталей служит для описания направленных локализованных связей. Гибридные орбитали обеспечивают максимальное перекрывание АО в направлении локализованных σ-связей.
2. Число гибридных орбиталей равно числу АО, участвующих в гибридизации.
3. Гибридизуются близкие по энергии валентные АО независимо от того, заполнены они в атоме полностью, наполовину или пусты.
4. В гибридизации участвуют АО, имеющие общие признаки симметрии.
Согласно табл. 3.3 гибридные орбитали дают молекулы с углами 180°, 120°, 109°28', 90°. Это правильные геометрические фигуры. Такие молекулы образуются, когда все периферические атомы в многоэлектронной молекуле (или ионе) одинаковы и их число совпадает с числом гибридных орбиталей. Однако, если число гибридных орбиталей больше числа связанных атомов, то часть гибридных орбиталей заселена электронными парами, не участвующими в образовании связи, – несвязывающими или неподеленными электронными парами.
| ||||||||||||||||||||||||||||||
| Таблица 3.3. Гибридные орбитали и геометрия молекул. |
В качестве примера рассмотрим молекулы NH3 и H2O. Атомы азота и кислорода склонны к sp3-гибридизации. У азота на sp3-ГО, поимо трех связывающих пар электронов, образующих связь с тремя атомами водорода, остается одна несвязывающая пара. Именно она, занимая одну sp3-ГО, искажает угол связи H–N–H до 107,3°. В молекуле H2O таких несвязывающих пар две, и угол H–O–H равен 104,5° (рис. 3.17).
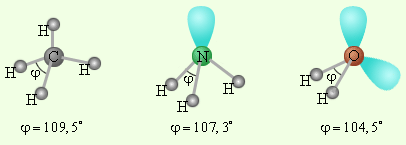 |
| Рисунок 3.17. Несвязывающие электронные пары и углы связи в молекулах NH3 и H2O в сравнении с молекулой CH4. |
Электроны связывающих и несвязывающих пар по-разному взаимодействуют между собой. Чем сильнее межэлектронное отталкивание, тем больше условная поверхность на сфере, занимаемый электронной парой. Для качественного объяснения экспериментальных фактов обычно считается, что несвязывающие пары занимают больший объем, чем связывающие, а объем связывающих пар тем меньше, чем больше электроотрицательности периферийных атомов (метод Гиллеспи).
Метод Гиллеспи–Найхолма.
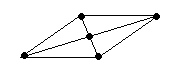
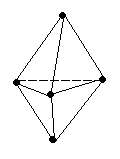
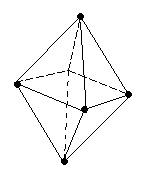
Этот метод основан на том, что реальная геометрия молекулы определяется не только гибридизацией АО, но и числом двухэлектронных двухцентровых связей (связывающих электронных пар) и наличием неподеленных электронных пар (Е). Тогда при одинаковой гибридизации молекула метана соответствует формуле CH4, аммиака – NH3E, воды – H2OE2. При этом каждая молекула представляет собой геометрическую фигуру, вписанную в сферу. Молекула будет иметь минимум энергии, если все связывающие электронные пары будут равноудалены друг от друга на поверхности сферы. Неподеленная электронная пара занимает на сфере большую площадь, что приводит к уменьшению валентного угла тем больше, чем больше в молекуле неподеленных электронных пар E. Рассмотрим структуры молекул от трехатомных до семиатомных (рис. 3.18).
Для трехатомной молекулы AX2 возможно единственное строение – линейное, четырехатомная молекула AX3 будет плоской в форме равностороннего треугольника, пятиатомная AX4 – тетраэдрической, шестиатомная AX5 – иметь форму треугольной бипирамиды, а семиатомная AX6 – форму октаэдра.
Иное дело – наличие в молекуле неподеленных электронных пар. В этом случае геометрия молекулы существенно меняется. Молекула AX2E будет уже не линейной, а угловой, AX3E будет иметь форму треугольной пирамиды, а AX2E2 вновь будет угловой, причем угол будет существенно меньше тетраэдрического (например, H2O). В молекуле AX4E возможная структура – треугольнопирамидальная. Молекула AX5E имеет структуру квадратной пирамиды, а молекула AX4E2 – квадрата.
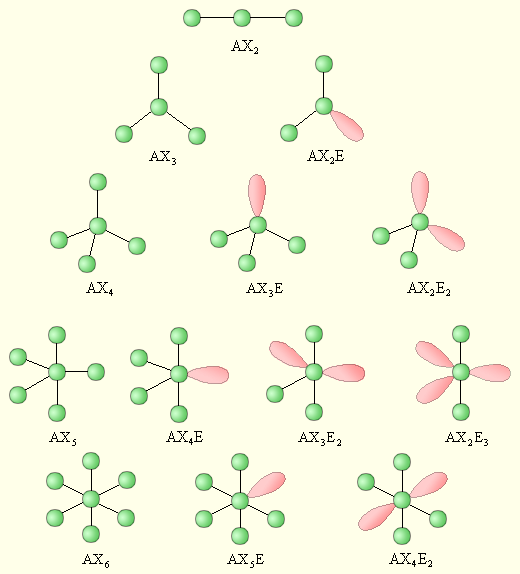 |
| Рисунок 3.18. |

Тема 4: Химическая термодинамика.
Цель:
1. Ознакомиться с определениями энтальпии (H), энтропии (S), потенциала Гиббса (G) и их стандартных величин.
2. Научиться записывать математически уравнения, связывающие следующие величины: ΔG и T, ΔH и ΔS; ΔG и K равновесия; ΔG° и E°.
3. Понимать, что характеризуют равенство ΔG°= 0 и неравенство ΔG°< 0, ΔG°> 0.
4. Знать при каких условиях энтальпийный фактор определяет самопроизвольное протекание химического процесса.
5. Знать при каких условиях энтропийный фактор определяет самопроизвольное протекание химического процесса.
6. Научиться записывать закон Гесса и его следствия.
7. Научиться записывать уравнение изотермы Вант-Гоффа для реакций.
Выполнить вопросы №14, №15 из теста.
Энтальпия (H).
Энтальпия системы (от греч. enthalpo нагреваю), однозначная функция H состояния термодинамической системы при независимых параметрах энтропии S и давлении P, связана с внутренней энергией U соотношением
|
где V – объем системы.
В химии чаще всего рассматривают изобарические процессы (P = const), и тепловой эффект в этом случае называют изменением энтальпии системы или энтальпией процесса:
|
|
Энтальпия имеет размерность энергии (кДж). Ее величина пропорциональна количеству вещества; энтальпия единицы количества вещества (моль) измеряется в кДж∙моль–1.
В термодинамической системе выделяющуюся теплоту химического процесса условились считать отрицательной (экзотермический процесс, ΔH < 0), а поглощение системой теплоты соответствует эндотермическому процессу, ΔH > 0.
Уравнения химических реакций с указанием энтальпии процесса называют термохимическими. Численные значения энтальпии ΔH указывают через запятую в кДж и относят ко всей реакции с учетом стехиометрических коэффициентов всех реагирующих веществ. Поскольку реагирующие вещества могут находиться в разных агрегатных состояниях, то оно указывается нижним правым индексом в скобках: (т) – твердое, (к) – кристаллическое, (ж) – жидкое, (г) – газообразное, (р) – растворенное. Например, при взаимодействии газообразных H2 и Cl2 образуются два моля газообразного HCl. Термохимическое уравнение записывается так:
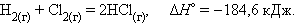 |
При взаимодействии газообразных H2 и O2 образующаяся H2O может находиться в трех агрегатных состояниях, что скажется на изменении энтальпии:
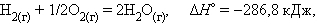 |
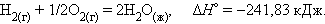 |
Приведенные энтальпии образования веществ и энтальпии реакций отнесены к стандартным условиям (P = 101,325 кПа) и взяты для температуры T = 298 K. Стандартное состояние термодинамической функции, например, энтальпии, обозначается нижним и верхним индексами: 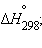 нижний индекс обычно опускают: Δ
нижний индекс обычно опускают: Δ 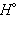 .
.
Стандартная энтальпия образования  – тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.
– тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.
Например, для реакций
| Реакция | Энтальпия образования |
| Na2O(т) + H2O(ж) = 2NaOH(т) | 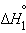 |
| 1/2Na2O(т) + 1/2H2O(ж) = NaOH(т) | 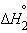 |
| Na(т) + 1/2O2(г) + 1/2H2(г) = NaOH(т) | 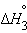 |
| 2Na(т) + O2(г) + H2(г)= 2NaOH(т) | 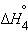 |
только 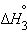 является стандартной энтальпией образования NaOH.
является стандартной энтальпией образования NaOH.
Энтальпия образования простых веществ принята равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298 K. Так, для йода 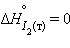 кДж∙
кДж∙ 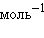 ,
, 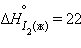 кДж∙
кДж∙ 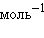 ,
, 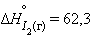 кДж∙
кДж∙ 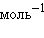 . Для углерода
. Для углерода 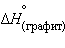 = 0 кДж∙
= 0 кДж∙ 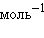 ,
, 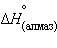 = 1,83 кДж∙
= 1,83 кДж∙ 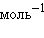 .
.
Стандартная энтальпия сгорания 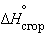 – тепловой эффект реакции сгорания одного моля вещества до образования высших оксидов. Для органических веществ – до
– тепловой эффект реакции сгорания одного моля вещества до образования высших оксидов. Для органических веществ – до 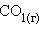 и
и 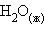 . Теплота сгорания негорючих веществ принимается равной нулю. Теплота сгорания топлива характеризует его теплотворную способность.
. Теплота сгорания негорючих веществ принимается равной нулю. Теплота сгорания топлива характеризует его теплотворную способность.
Энтальпия растворения складывается из теплоты разрушения кристаллической решетки (ΔHреш > 0) и теплоты гидратации (сольвататции для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава – гидратов (сольватов) (ΔHгидр < 0).
В зависимости от соотношения значений ΔHреш и ΔHгидр энтальпия растворения может иметь как положительное, так и отрицательное значение.
Так, энтальпия растворения КОН – отрицательная величина и характеризует экзотермический процесс:
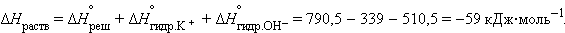 |
Растворение же 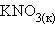 – эндотермический процесс (ΔH = 35,9 кДж∙
– эндотермический процесс (ΔH = 35,9 кДж∙ 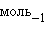 ), так как на разрушение кристаллической решетки (
), так как на разрушение кристаллической решетки ( 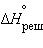 = 684,5 кДж∙
= 684,5 кДж∙ 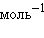 ) затрачивается больше энергии, чем выделяется при гидратации ионов
) затрачивается больше энергии, чем выделяется при гидратации ионов 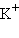 и
и 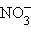 : –339 и –309,6 кДж∙моль–1 соответственно.
: –339 и –309,6 кДж∙моль–1 соответственно.
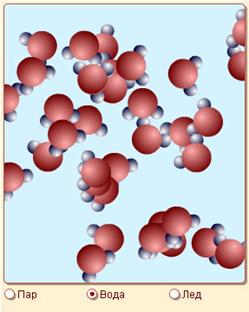 |
| Модель 4.7. Агрегатные состояния. С помощью этой модели вы можете подробно рассмотреть микроструктуру воды в различных агрегатных состояниях. В твердой форме (лед) для молекул воды доступны лишь вращательные и колебательные движения, поступательные движения на заметные расстояния невозможны. Обратите внимание на четкую кристаллическую структуру льда, а также на ориентацию молекул (атомы водорода одних молекул направлены в сторону атомов кислорода других). При этом каждая молекула воды соединена с четырьмя ближайшими к ней другими молекулами. Образуемые при этом пустоты в структуре льда приводят к уменьшению его плотности по сравнению с жидкой водой. В жидкой форме вода все еще существует как единое целое (сохраняет объем), расстояния между молекулами по порядку величины совпадают с размерами самих молекул. Однако возможны далекие по сравнению с этими размерами смещения молекул от своих начальных положений, из-за этого не сохраняются ни взаимные ориентации молекул, ни форма жидкости как целого. Наконец, в газе молекулы максимально обособлены друг от друга, и длина свободного пробега молекулы гораздо больше ее размеров. |
Стандартная энтальпия нейтрализации 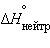 – энтальпия реакции взаимодействия сильных кислот и оснований с образованием одного моля
– энтальпия реакции взаимодействия сильных кислот и оснований с образованием одного моля 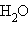 при стандартных условиях.
при стандартных условиях.
| HCl + NaOH = NaCl + H2O; |
| H+ + OH– = H2O, ΔH ° = –55,9 кДж∙моль–1. |
Для концентрированных растворов сильных электролитов 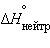 может быть различным из-за изменения значения
может быть различным из-за изменения значения 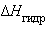 их ионов при разбавлении.
их ионов при разбавлении.
Стандартная энтальпия реакции ΔH ° – тепловой эффект реакции определенного числа молей реагентов, задаваемого уравнением реакции при стандартных условиях. Например, для реакции
| 3H2O(ж) + 2Fe(т) → Fe2O3(т) + 3H2(г), ΔH ° = 34 кДж |
ΔH ° относится целиком к реакции, как она записана.
Стандартная энтальпия разрыва связи 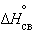 (называемая также энергией связи
(называемая также энергией связи 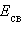 ) – энергия, поглощаемая при разрыве связей двух атомов одного моля вещества, находящегося в газообразном состоянии при 298 К:
) – энергия, поглощаемая при разрыве связей двух атомов одного моля вещества, находящегося в газообразном состоянии при 298 К:
| HCl(г) → H(г) + Cl(г), ΔH ° = 429,7 кДж. |
Средние стандартные энтальпии связи могут быть определены для индивидуального соединения или путем усреднения значений, найденных для целых классов соединений.
Энтропия (S).
Изменение энтальпии системы не может служить единственным критерием самопроизвольного осуществления химической реакции, поскольку многие эндотермические процессы протекают самопроизвольно. Иллюстрацией этого служит растворение некоторых солей (например, NH4NO3) в воде, сопровождающееся заметным охлаждением раствора. Необходимо учитывать еще один фактор, определяющий способность самопроизвольно переходить из более упорядоченного к менее упорядоченному (более хаотичному) состоянию.
Энтропия (S) – термодинамическая функция состояния, которая служит мерой беспорядка (неупорядоченности) системы. Возможность протекания эндотермических процессов обусловлена изменением энтропии, ибо в изолированных системах энтропия самопроизвольно протекающего процесса увеличивается ΔS > 0 (второй закон термодинамики).
Л. Больцман определил энтропию как термодинамическую вероятность состояния (беспорядок) системы W. Энтропия связана с термодинамической вероятностью соотношением:
|
Размерность энтропии 1 моля вещества совпадает с размерностью газовой постоянной R и равна Дж∙моль–1∙K–1. Изменение энтропии в необратимых и обратимых процессах передается соотношениями ΔS > Q / T и ΔS = Q / T. Например, изменение энтропии плавления равно теплоте (энтальпии) плавления ΔSпл = ΔHпл/Tпл Для химической реакции изменение энтропии аналогично изменению энтальпии
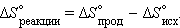 |
Здесь ΔS° соответствует энтропии стандартного состояния. Стандартные энтропии простых веществ не равны нулю. В отличие от других термодинамических функций энтропия идеально кристаллического тела при абсолютном нуле равна нулю (постулат Планка), поскольку W = 1.
Энтропия вещества или системы тел при определенной температуре является абсолютной величиной. В табл. 4.1 приведены стандартные энтропии S° некоторых веществ.
| ||||||||||||||||||||||||||||||||||||||||||||
| Таблица 4.1. Стандартные энтропии некоторых веществ. |
Из табл. 4.1 следует, что энтропия зависит от:
1. Агрегатного состояния вещества. Энтропия увеличивается при переходе от твердого к жидкому и особенно к газообразному состоянию (вода, лед, пар).
2. Изотопного состава (H2O и D2O).
3. Молекулярной массы однотипных соединений (CH4, C2H6, н-C4H10).
4. Строения молекулы (н-C4H10, изо-C4H10).
5. Кристаллической структуры (аллотропии) – алмаз, графит.
Наконец, рис. 4.3 иллюстрирует зависимость энтропии от температуры.
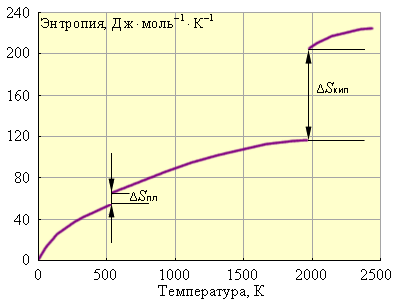 |
| Рисунок 4.3. Зависимость энтропии от температуры для свинца: ΔSпл = 8 Дж·моль–1·К–1; Tпл = 600,5 К; ΔSкип = 88 Дж·моль–1·К–1; Tкип = 2013 К. |
Следовательно, стремление системы к беспорядку проявляется тем больше, чем выше температура. Произведение изменения энтропии системы на температуру TΔS количественно оценивает эту тендецию и называется энтропийным фактором.
Энергия Гиббса (G).
Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным TΔS, обусловленным увеличением беспорядка в системе вследствие роста ее энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж):
|
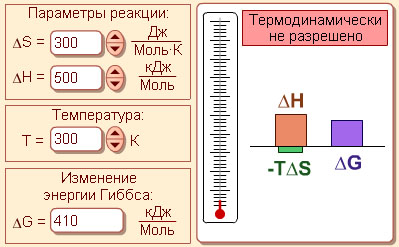 |
| Модель 4.10. Энергия Гиббса. Эта модель демонстрирует понятие термодинамически разрешенной реакции, а также связь этого понятия с основными термодинамическими функциями. Вы можете изменять параметры модельной реакции при помощи полей ввода с кнопками прокрутки и видеть, как в зависимости от них изменяется энергия Гиббса, поглощаемая в реакции или же, наоборот, выделяемая в ней. Все актуальные в данном случае термодинамические потенциалы (энтальпия, энергия Гиббса), а также произведение энтропии и температуры изображены на столбиковой диаграмме в окне в правой части модели. Исследуя модель, вы увидите, что только при отрицательном приросте энергии Гиббса реакция термодинамически разрешена, то есть ее протекание возможно. Однако следует помнить, что скорость протекания реакции в неблагоприятных условиях может быть слишком низкой, так что потребуется повышение температуры или добавление катализатора, чтобы можно было получить заметное количество продуктов реакции. Обратите внимание, что повышение температуры может как сделать реакцию из разрешенной запрещенной, так и наоборот. |
При ΔG < 0 реакция термодинамически разрешена и система стремится к достижению условия ΔG = 0, при котором наступает равновесное состояние обратимого процесса; ΔG > 0 указывает на то, что процесс термодинамически запрещен (рис. 4.4).
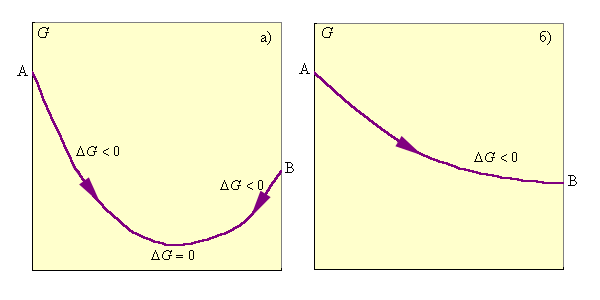 |
| Рисунок 4.4. Изменение энергии Гиббса: а – обратимый процесс; б – необратимый процесс. |
Записав уравнение (4.2) в виде ΔH = ΔG + TΔS, получим, что энтальпия реакции включает свободную энергию Гиббса и «несвободную» энергию ΔS · T. Энергия Гиббса, представляющая собой убыль изобарного (P = const) потенциала, равна максимальной полезной работе. Уменьшаясь с течением химического процесса, ΔG достигает минимума в момент равновесия (ΔG = 0). Второе слагаемое ΔS · T (энтропийный фактор) представляет ту часть энергии системы, которая при данной температуре не может быть превращена в работу. Эта связанная энергия способна лишь рассеиваться в окружающую среду в виде тепла (рост хаотичности системы).
Итак, в химических процессах одновременно изменяются энергетический запас системы (энтальпийный фактор) и степень ее беспорядка (энтропийный фактор, не совершающая работу энергия).
Анализ уравнения (4.2) позволяет установить, какой из факторов, составляющих энергию Гиббса, ответственен за направление протекания химической реакции, энтальпийный (ΔH) или энтропийный (ΔS · T).
· Если ΔH < 0 и ΔS > 0, то всегда ΔG < 0 и реакция возможна при любой температуре.
· Если ΔH > 0 и ΔS < 0, то всегда ΔG > 0, и реакция с поглощением теплоты и уменьшением энтропии невозможна ни при каких условиях.
· В остальных случаях (ΔH < 0, ΔS < 0 и ΔH > 0, ΔS > 0) знак ΔG зависит от соотношения ΔH и TΔS. Реакция возможна, если она сопровождается уменьшением изобарного потенциала; при комнатной температуре, когда значение T невелико, значение TΔS также невелико, и обычно изменение энтальпии больше TΔS. Поэтому большинство реакций, протекающих при комнатной температуре, экзотермичны. Чем выше температура, тем больше TΔS, и даже эндотермические реакции становятся осуществляемыми.
Проиллюстрируем эти четыре случая соответствующими реакциями:
| 1. | ΔH < 0 ΔS > 0 ΔG < 0 | C2H5–O–C2H5 + 6O2 = 4CO2 + 5H2O (реакция возможна при любой температуре) |
| 2. | ΔH > 0 ΔS < 0 ΔG > 0 | реакция невозможна |
| 3. | ΔH < 0 ΔS < 0 ΔG > 0, ΔG < 0 | N2 + 3H2 = 2NH3 (возможна при низкой температуре) |
| 4. | ΔH > 0 ΔS > 0 ΔG > 0, ΔG < 0 | N2O4(г) = 2NO2(г) (возможна при высокой температуре). |
Для оценки знака ΔG реакции важно знать величины ΔH и ΔS наиболее типичных процессов. ΔH образования сложных веществ и ΔH реакции лежат в пределах 80–800 кДж∙ 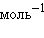 . Энтальпия реакции сгорания
. Энтальпия реакции сгорания 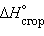 всегда отрицательна и составляет тысячи кДж∙
всегда отрицательна и составляет тысячи кДж∙ 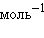 . Энтальпии фазовых переходов обычно меньше энтальпий образования и химической реакции Δ
. Энтальпии фазовых переходов обычно меньше энтальпий образования и химической реакции Δ 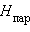 – десятки кДж∙
– десятки кДж∙ 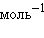 , Δ
, Δ 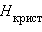 и Δ
и Δ 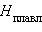 равны 5–25 кДж∙
равны 5–25 кДж∙ 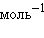 .
.
Зависимость ΔH от температуры выражается соотношением ΔHT = ΔH° + ΔCp · ΔT, где ΔCp – изменение теплоемкости системы. Если в интервале температур 298 К – Т реагенты не претерпевают фазовых превращений, то ΔCp = 0, и для расчетов можно пользоваться значениями ΔH°.
Энтропия индивидуальных веществ всегда больше нуля и составляет от десятков до сотен Дж∙моль–1K–1 (табл. 4.1). Знак ΔG определяет направление реального процесса. Однако для оценки осуществимости процесса обычно пользуются значениями стандартной энергии Гиббса ΔG°. Величина ΔG° не может использоваться в качестве критерия вероятности в эндотермических процессах со значительным возрастанием энтропии (фазовые переходы, реакции термического разложнения с образованием газообразных веществ и др.). Такие процессы могут быть осуществлены за счет энтропийного фактора при условии 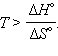
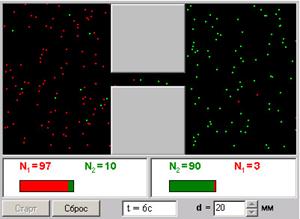 |
| Модель 4.11. Диффузия газов. |
Моделируется процесс диффузии газов через трубку, соединяющую две половины сосуда. Модель позволяет наблюдать диффузию при различных размерах соединительной трубки. Диффузией называется процесс самопроизвольного выравнивания концентраций молекул жидкости или газа в различных частях объема. Диффузия приближает систему к состоянию термодинамического равновесия. Если в двух половинках сосуда находятся разные газы (при одинаковых температуре и давлении) и между ними нет разделяющей перегородки, то вследствие теплового движения молекул возникает процесс взаимопроникновения газов. Этот процесс и называется диффузией. Скорость диффузии сильно зависит от длины свободного пробега молекул, то есть от среднего расстояния, которое пролетают молекулы между двумя последовательными соударениями с другими молекулами. Процесс диффузии протекает достаточно медленно, если длина свободного пробега намного меньше размеров сосуда.
Взаимопроникновение молекул из одной половины сосуда в другую, соединенных трубкой, также называют диффузией. Скорость процесса в этом случае сильно зависит от геометрических размеров соединительной трубки.
В данной компьютерной модели демонстрируется процесс взаимной диффузии двух различных газов, первоначально находящихся в двух сосудах, через соединительную трубку. Пронаблюдайте качественно зависимость скорости диффузии от диаметра соединительной трубки.
Закон Гесса.
Пользуясь табличными значениями 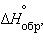
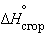 и
и 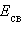 , можно рассчитать энтальпии различных химических процессов и фазовых превращений. Основанием для таких расчетов является закон Гесса, сформулированный петербургским профессором Г. И. Гессом (1841 г.): «Тепловой эффект (энтальпия) процесса зависит только от начального и конечного состояния и не зависит от пути перехода его из одного состояния в другое».
, можно рассчитать энтальпии различных химических процессов и фазовых превращений. Основанием для таких расчетов является закон Гесса, сформулированный петербургским профессором Г. И. Гессом (1841 г.): «Тепловой эффект (энтальпия) процесса зависит только от начального и конечного состояния и не зависит от пути перехода его из одного состояния в другое».
Анализ закона Гесса позволяет сформулировать следующие следствия:
1. Энтальпия реакции равна разности сумм энтальпий образования конечных и начальных участников реакций с учетом их стехиометрических коэффициентов.
| 2. ΔH = ΣΔHобр.конечн – ΣΔHобр.нач |
3. Энтальпия реакции равна разности сумм энтальпий сгорания начальных и конечных реагентов с учетом их стехиометрических коэффициентов.
| 4. ΔH = ΣΔHсгор.нач – ΣΔHсгор.конечн |
5. Энтальпия реакции равна разности сумм энергий связей Eсв исходных и конечных реагентов с учетом их стехиометрических коэффициентов.
6. В ходе химической реакции энергия затрачивается на разрушение связей в исходных веществах (ΣEисх) и выделяется при образованиии продуктов реакции (–ΣEпрод). Отсюда
| 7. ΔH° = ΣEисх – ΣEпрод |
8. Следовательно, экзотермический эффект реакции свидетельствует о том, что образуются соединения с более прочными связями, чем исходные. В случае эндотермической реакции, наоборот, прочнее исходные вещества.
9. При определении энтальпии реакции по энергиям связей уравнение реакции пишут с помощью структурных формул для удобства определения числа и характера связей.
10. Энтальпия реакции образования вещества равна энтальпии реакции разложения его до исходных веществ с обратным знаком.
| 11. ΔHобр = –ΔHразл |
12. Энтальпия гидратации равна разности энтальпий растворения безводной соли 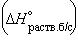 и кристаллогидрата
и кристаллогидрата 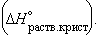
Из вышесказанного видно, что закон Гесса позволяет обращаться с термохимическими уравнениями как с алгебраическими, т. е. складывать и вычитать их, если термодинамические функции относятся к одинаковым условиям.
Например, диоксид углерода можно получить прямым синтезом из простых веществ (I) или в две стадии через промежуточный продукт (II):
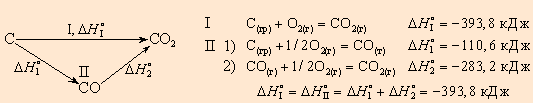 |
| Рисунок 4.1. Энтальпия первого пути равна сумме энтальпий отдельных стадий второго пути. |
Выполнить вопрос из теста №14.
Химическое равновесие.
Для определения величины ΔG в условиях, отличных от стандартных, используют уравнение зависимости изобарно-изотермического потенциала от концентрации и температуры.
Используя соотношения (4.1) и (4.2), получаем:
|

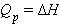
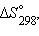 (Дж∙моль–1∙K–1)
(Дж∙моль–1∙K–1)