Водород. Общая характеристика. Взаимодействие водорода с кислородом, галогенами, активными Ме и оксидами. Бинарные соединения водорода.

Водород занимает первое место в ПСМ. Он имеет простейшее строение атома: ядро атома окружено электронным облаком. Электронная конфигурация 1s¹. В одних условиях Н₂ проявляет Ме св-ва (отдает ), в других-неМе (принимает ).

Нахождение: содержится в воде, во все органических соед. Концентрация в организме человека ≈ 10%.

Физические св-ва: Н₂-самый легкий газ, без цвета, запаха и вкуса. Мало растворим в воде. При t-252,8º и атмосферном давлении переходит в жидкое состояние.

Известны три изотопа водорода: протий 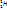, дейтерий 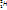, тритий .

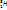Химические св-ва: 1. Р-ции с простыми в-вами.

▪с кислородом: 2Н₂⁰ +О₂=2Н₂О +572кдж

▪с S при нагревании (150-300º): Н₂⁰ +S↔Н₂S

▪cF: Н₂⁰ +F₂=2НF

▪с N при повышенном давлении и нагревании в присутствии kat: 3Н₂⁰+N₂↔2NH₃

▪как окисл-ль взаимод. только с активными Ме, образуя гидриды металлов: 2Na+ Н₂⁰=2NaH

2. Р-ции со сложными в-вами.

▪при ↑ tº водород может восстанавливать оксиды метеллов: CuO+H₂=Cu+ H₂O

▪способен присоединятся ко многим орг соед: CH₂=CH₂+H₂→CH₃-CH₃

Применение: Без воды жизнь не возможна!

Водород образует 2 бинарных соединения с кислородом: H₂O и H₂O₂

Основные положения квантовой механики: квантовый характер поглощения и излучения энергии (Планк), корпускулярно-волновой дуализм микрочастиц (уравнение Де-Бройля), принцип неопределенности, волновая функция и представление о ее расчете на основании уравнения Шредингера.

Квантовый характер излучения и поглощения энергии электромагнитного поля был постулирован Планком в 1900 году для объяснения свойств теплового излучения.

Квантовый характер явлений излучения и поглощения доказывает наличие у микросистем, в том числе у электромагнитного поля, отдельных энергетических уровней и невозможность микросистемы обладать произвольной величиной энергии.

В 1924 г французский физик Луи де Бройль выдвинул смелую гипотезу, согласно которой корпускулярно-волновой дуализм имеет универсальный характер. Согласно гипотезе де Бройля каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы остаются такими же, как и в случае электромагнитного излучения. Напомним, что энергия Eи импульс pфотона связаны с круговой частотой и длиной волны 𝜆соотношениями: E=h𝜔, p=kh=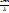

Стационарное уравнение Шрёдингера

Пусть амплитуда вероятности нахождения частицы в точке М. Стационарное уравнение Шрёдингера позволяет ее определить. Функция 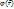удовлетворяет ур-ие: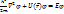

где —оператор Лапласа, аU=U — потенциальная энергия частицы как функция .

Решение стационарного уравнения

Пусть E и U две постоянные, независимые от .Записав стационарное уравнение как:

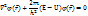
Если E-U>0, то:

Решение стационарного ур-ия в случае, когда E-U>0

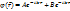
где: 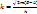— модуль волнового вектора; A и B — две постоянные, определяющиеся граничными условиями.

Если E-U<0, то: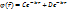

где 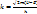— — модуль волнового вектора; C и D — две постоянные, также определяющиеся граничными условиями.