Квантовые числа. Понятия о s,p,d,f-элементах. Порядок заполнения электронных оболочек атомов.

Состояние электрона в атоме характеризуется четырьмя квантовыми числами:

1 Главное квантовое число (n) или радиус круговой боровской орбиты, характеризует с точки зрения квантовой механики энергетический уровень электрона и размеры, и плотность электронного облака. Число

энергетических уровней в атоме равно номеру периода, в котором располагается данный элемент в периодической таблице Д.И. Менделеева. Главное квантовое число принимает целочисленные значения n = 1, 2 ,3 … до

бесконечности. Электроны с одинаковым значением n обладают одинаковой энергией и образуют один и тот же энергетический уровень. Энергетические уровни кроме числового значения обозначаются и буквами

1 2 3 4

K L M N

2 Согласно квантово-механическим расчетам электронные облака отличаются не только размерами, но и формой. Форму электронного облака характеризует орбитальное (азимутальное) квантовое число (l).

Различная форма электронных облаков обуславливает изменение энергии электрона в пределах одного энергетического уровня, т.е. происходит расщепление энергетического уровня на так называемые энергетические подуровни. Орбитальное квантовое число принимает целочисленные значения от 0 … до (n – 1).

n 1 2 3 4

l 0 0, 1 0, 1, 2 0, 1, 2, 3

Кроме числового значения орбитальное квантовое число обозначается и буквами: l = 0 – s-электронное об-

лако, l = 1 – p-электронное облако, l = 2 – d-электронное облако, l = 3 – f-электронное облако.

3 Изучение спектров атомов, показало, что в магнитном и электромагнитном полях спектральные линии в

атомных спектрах расщепляются на более тонкие компоненты. Взаимодействие магнитного поля электрона c

внешним магнитным полем определяет пространственное расположение орбиты электрона. Пространственную

ориентацию электронных облаков характеризует магнитное квантовое число (ml). Магнитное квантовое число принимает целочисленные значения от – l через 0 до + l, т.е. магнитное квантовое число показывает, на сколько энергетических ячеек делится энергетический подуровень.

Квантовые числа n, l, ml – характеризуют движение электрона в около ядерном пространстве. Состояние электрона в атоме, описываемое значениями трех квантовых чисел n, l, ml называют энергетической ячейкой или атомной электронной орбиталью. Атомная орбиталь – это трехмерный объект, это пространство вокруг ядра атома, в котором находится электрон.

4 Помимо движения вокруг ядра, электрон характеризуется собственным внутренним движением, которое очень сложно, но можно сказать, что электрон движется вокруг собственной оси по часовой или против часовой стрелки. Это движение характеризуют спиновым квантовым числом или спином (S). Если электрон движется по часовой стрелке, то S = +1/2. Если против часовой стрелки то S = –1/2. Набор четырех квантовых чисел

определяет положение электрона в атоме. Электрон, находящийся на орбитале один, называется неспаренным.

Следовательно, электронная оболочка атома выглядит следующим образом:

Периодические функции.

Периодическая функция ― функция, повторяющая свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода функции).

Говоря более формально, функция периодична, если существует такое число T≠0 (период), что на всей области определения функции выполняется равенство .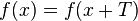

Все тригонометрические функции являются периодическими.

Формальное определение

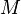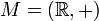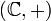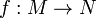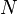Пусть есть абелева группа (обычно предполагается — вещественные числа с операцией сложения или — комплексные числа). Функция (где — произвольное множество её значений) называется периодической с периодом 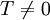, если справедливо

.

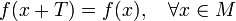Если это равенство не выполнено ни для какого 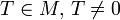, то функция 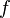называется апериодической.

Если для функции 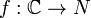существуют два периода 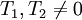, отношение которых не равно вещественному числу, то есть 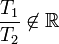, то 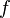называется двоякопериодической функцией. В этом случае значения 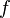на всей плоскости определяются значениями в параллелограмме, натянутом на .

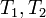Замечание

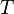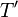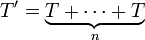Период функции определён неоднозначно. В частности, если — период, то и любой элемент вида (или 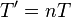, если в области определения функции определена операция умножения), где 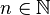— произвольное натуральное число, также является периодом.

Множество всех периодов функции образует аддитивную группу.

Однако если у множества периодов 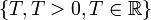имеется наименьшее значение, то оно называется основным (или главным) периодом функции.

Примеры

• Вещественные функции синус и косинус являются периодическими с основным периодом 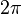, так как

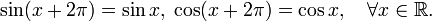
• Функция, равная константе 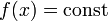, является периодической, и любое ненулевое число является её периодом. Основного периода функция не имеет.

• Функция Дирихле является периодической, её периодом является любое ненулевое рациональное число. Основного периода она также не имеет.

• Функция 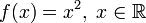является апериодической.