Растворы электролитов. Электролитическая диссоциация.
Буферные растворы
6.1 Электролитическая диссоциация
Законы Рауля и Вант-Гоффа, описывающие свойства идеальных растворов (температуру их кипения, замерзания и др. см. тему «Общие свойства растворов»), оказались для растворов одних веществ вполне удовлетворительными моделями их реальных свойств, для других веществ расчетные и экспериментальные свойства заметно различались.
Для согласования расчетных и экспериментальных данных по осмосу Вант-Гофф ввел коэффициент, названный изотоническим коэффициентом (i):
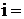 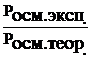 | (6.1.1) |
Т.е., если рассчитанную величину осмотического давления (Росм. теор.) умножить на i, то получим реальную, измеренную величину (Росм. эксп.).
С. Аррениус, сопоставив расчетные и экспериментальные данные по другим коллигативным свойствам одних и тех же растворов, установил, что коэффициенты, подобные i, для них примерно одинаковы:
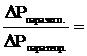
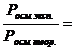
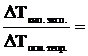
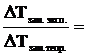 i
i
В таком случае логично было предположить, что причина несоответствия рассчитанных и экспериментальных величин – одна и та же.
Было установлено, что для одних растворов i » 1 (т.е. такие растворы по свойствам близки к идеальным растворам). Для других растворов i < 1, что можно объяснить ассоциацией (связыванием) частиц растворенного вещества. Наибольшее удивление вызвали растворы, для которых изотонический коэффициент был больше единицы, нередко в несколько раз. Каким образом количество растворенного вещества оказалось большим, чем его растворили?
Объяснение могло быть только одно: частицы некоторых веществ (молекулы или др.) при растворении не только распределяются среди молекул растворителя, но и распадаются на более мелкие частицы (диссоциируют). В результате общее число частиц (Nобщее) увеличивается по сравнению с числом растворенных (N0). По этой причине реальные свойства растворов (  Ткип, Росм. и др.) оказываются большими по сравнению с рассчитанными. По-видимому, изотонический коэффициент и показывает, во сколько раз число частиц в растворе (Nобщее) отличается от того, которое растворили (N0), т.е. i = Nобщее/N0.
Ткип, Росм. и др.) оказываются большими по сравнению с рассчитанными. По-видимому, изотонический коэффициент и показывает, во сколько раз число частиц в растворе (Nобщее) отличается от того, которое растворили (N0), т.е. i = Nобщее/N0.
Как оказалось, растворы, для которых i > 1, объединяет еще одно общее свойство – они электропроводны.
Теория электролитической диссоциации Аррениуса (окончательный вариант – 1887 г.) включала три основных положения:
1) В растворах электролитов происходит самопроизвольный распад – диссоциация молекул на ионы, в результате чего раствор становится электропроводным;
2) Осмотическое давление, температуры кипения и замерзания растворов зависят не только от аналитической концентрации электролита, но и от степени его диссоциации (α). Степень диссоциации – это отношение числа частиц растворенного вещества, которые продиссоциировали (Nдис), к исходному числу частиц растворенного вещества (No):
| α = Nдис/No | (6.1.2) |
3) Для одного и того же растворенного вещества степень диссоциации увеличивается по мере разбавления раствора.
Поскольку свойства растворов зависят от концентрации растворенных частиц, а она, в свою очередь, зависит от степени диссоциации растворенного вещества, то, по-видимому, должна быть связь между степенью диссоциации электролита и изотоническим коэффициентом.
Действительно, если растворили N0 молекул вещества, и степень его диссоциации α, то продиссоциируют αN0 молекул. Если каждая молекула при диссоциации образует z ионов, то всего образуется zαN0 ионов. Недиссоциированными останутся (N0 – αN0) молекул. В результате в растворе окажется в виде молекул и ионов растворенного вещества (Nобщее):
Nобщее = (N0 – αN0) + zαN0 = N0(1 + αz – α).
Подставив это выражение в уравнение (6.1.1), получим:
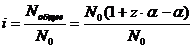 , откуда α =
, откуда α = 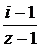
Например, если имеется раствор бинарного электролита (т.е. z = 2), и для него определили I = 1,2; то степень диссоциации этого электролита:
α = (1,2 – 1)/(2 – 1) = 0,2 (или 20 %).
Сильный электролит диссоциирует полностью и для него α = 1.
Изотонический коэффициент для сильного электролита показывает число ионов, на которые он диссоциирует:
HCl ® H+ + Cl– i = 2
Ca(NO3)2 ® Ca2+ + 2NO3– i = 3
Факторы, влияющие на электролитическую диссоциацию веществ.
Природа растворенного вещества
К электролитам относятся вещества с ионной кристаллической решеткой и вещества, состоящие из молекул с полярной или легко поляризуемой связью.
К сильным электролитам относятся большинство солей, гидроксиды щелочных и щелочноземельных металлов, а также некоторые кислоты: галогеноводородные (кроме HF), азотная, хлорная, хлорноватая, серная и др. (подробнее см. далее).
Влияние природы растворителя на диссоциацию электролитов
Источник энергии, необходимой для разрыва химических связей в растворяемом веществе – это взаимодействие растворяемого вещества с растворителем. Одни и те же вещества проявляют свойства сильных электролитов в одних растворителях и слабых – в других. Так, например, в воде хлороводород – сильный электролит, а в бензоле – слабый. Гидроксиды щелочных металлов полностью диссоциируют в воде, но различаются по силе в спиртовых растворах.
Чаще всего наибольшая степень диссоциации проявляется в растворителях с большой диэлектрической проницаемостью (ε), высокой сольватирующей способностью и малой вязкостью. К таким растворителям в первую очередь относится вода.
Влияние температуры на диссоциацию электролитов
«Диссоциация» сопровождается разрывом химических связей (ионных или ковалентных), что требует энергетических затрат, и поэтому увеличение температуры должно способствовать диссоциации, что в большинстве случаев и наблюдается.
На самом деле ситуация более сложная. Ионы – продукты диссоциации электролита – в результате ионно-молекулярного взаимодействия могут образовывать ассоциаты с растворителем (рисунок 6.1.1).
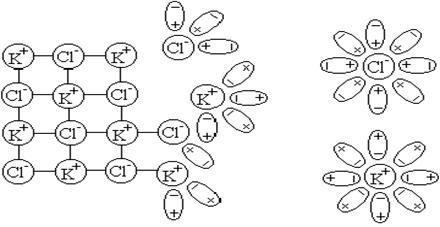
Рисунок 6.1.1 – Схема растворения (гидратации) хлорида калия
Образование сольватов – процесс экзотермический, поэтому при увеличении температуры сольваты разрушаются.
6.2 Диссоциация (ионизация) сильных электролитов
Сильные электролиты в растворах диссоциируют практически полностью (не подчиняются закону действующих масс), что отражают соответствующим знаком «®» в уравнении реакции (односторонний процесс, нет равновесия):
Ca(OH)2 ® Ca2+ + 2OH–
Cr2(SO4)3 ® 2Cr3+ + 3SO42–
H2SO4 ® 2H+ + SO42–
Концентрацию ионов в растворах сильных электролитов рассчитывают по уравнениям их диссоциации как для реакций, протекающих необратимо:
KatxAy ® xKatY+ + yAx–
В этом уравнении KatxAy – структурная (формульная) единица электролита, а KatY+, Ax– – его катион и анион, x, y – число катионов и анионов соответственно в формульной единице электролита.
Пример 1
Рассчитать концентрацию, моль/л, продуктов диссоциации
в 0,1 М растворе серной кислоты.
Решение: уравнение диссоциацииH2SO4 ® 2H+ + SO42–
Из уравнения видно, что при диссоциации 1 моль H2SO4 образуются
2 моль ионов водорода и 1 моль сульфат-ионов; следовательно,
С(H+) = 2∙С(H2SO4) = 0,1·2 = 0,2 моль/л, С(SO42–) = C(H2SO4) = 0,1 моль/л
Пример 2
Рассчитать концентрацию, моль/л, сульфата хрома(III) и ионов Cr3+, если молярная концентрация ионов SO42– равна 0,6 моль/л.
Решение: уравнение диссоциации Cr2(SO4)3 ® 2Cr3+ + 3SO42–
Из уравнения видно, что при диссоциации 1 моль Cr2(SO4)3 образуются 2 моль ионов хрома и 3 моль сульфат-ионов.
Следовательно, С(Cr2(SO4)3) = 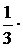 С(SO42–) =
С(SO42–) = 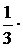 0,6 = 0,2 моль/л;
0,6 = 0,2 моль/л;
С(Cr3+) = 2∙С(Cr2(SO4)3) = 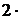 0,2 = 0,4 моль/л.
0,2 = 0,4 моль/л.
6.3 Диссоциация слабых электролитов. Константа диссоциации.
Степень диссоциации
Электролиты, которые диссоциируют не полностью, называют слабыми. При их диссоциации устанавливается равновесие между ионами – продуктами диссоциации и нераспавшимися молекулами (или сложными ионами), подчиняющееся закону действующих масс (см. тему «Химическое равновесие»). Эту особенность отражают в уравнении соответствующим знаком ««» – равновесный процесс:
HA « H+ + A– Kдис. = 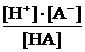 (6.2)
(6.2)
Константу равновесия диссоциации слабого электролита называют константой диссоциации.
Константа диссоциации количественно характеризует силу электролита: чем слабее электролит, тем меньше константа диссоциации.
Для слабых кислот константу принято обозначать Ка (от англ. «acid» кислота), а для слабых оснований – Kb (от англ. «base» – основание).
Примеры
Диссоциация плавиковой кислоты: HF « H+ + F–
Ka = 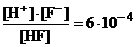
Диссоциация аммиака в водном растворе: NH3·H2O « NH4+ + OH–
Kb = 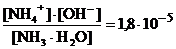
Слабые многоосновные кислоты, HxA, и многокислотные основания, Me(OH)x, диссоциируют ступенчато.
Каждая ступень диссоциации характеризуется своей константой.
Например, в растворе ортофосфорной кислоты устанавливаются следующие равновесия.
Первая ступень диссоциации:
H3PO4 « H+ + H2PO4–
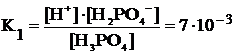
Вторая ступень диссоциации:
H2PO4– « H+ + HPO42–
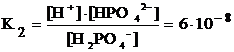
Третья ступень диссоциации:
HPO42– « H+ + PO43–
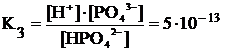
Константы диссоциации слабых электролитов приводятся в справочниках (одновременно это проверка, к сильным или слабым относится электролит: если слабый, то его константа, меньшая единицы, приведена в справочнике).
6.4 Расчет материального баланса в реакциях диссоциации слабых
электролитов. Электролитическая диссоциация воды; pH и pOH водных растворов
Уравнение диссоциации воды H2O « H+ + OH–
Константа равновесия (константа диссоциации воды):
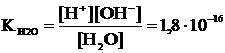 | (6.3.1) |
Из величины константы видно, что степень диссоциации воды очень мала, и поэтому можно считать, что [H2O] » C(H2O) = 1000/18 = 55,6 моль/л.
Тогда постоянной величиной (константой) можно считать
KH2O [H2O] » KH2O ∙C(H2O) » [H+][OH–] » 1,8·10–16·55,6 » 1·10–14
Произведение [H+][OH–] назвали ионным произведением воды и обозначили Kw:
| Kw = [H+][OH–] = 1·10–14 | (6.3.2) |
Из ионного произведения воды следует, что в воде и водных растворах любых веществ произведение равновесных молярных концентраций ионов H+ и OH– – величина постоянная (при постоянстве температуры) и называется ионным произведением воды (закон действующих масс применительно к диссоциации воды). При 298 К (25 0С) Kw = 1·10–14.
В чистой воде [H+] = [OH–] = 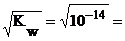 10–7 моль/л. В растворах кислот [H+] > [OH–], т.е. [H+] > 10–7 моль/л, [OH–] < 10–7 моль/л.
10–7 моль/л. В растворах кислот [H+] > [OH–], т.е. [H+] > 10–7 моль/л, [OH–] < 10–7 моль/л.
Примеры
1) Рассчитать концентрацию, моль/л, ионов [H+] и [OH–] в 0,1 М растворе серной кислоты.
Решение: H2SO4 ® 2H+ + SO42–
Из уравнения реакции видно, что концентрация ионов H+ в 2 раза больше концентрации кислоты, т.е. С(H+) = 0,1·2 = 0,2 моль/л (ионами H+ из воды можно пренебречь).
Концентрацию ионов OH–, рассчитаем из ионного произведения воды: Kw = [H+][OH–] = 1·10–14: [OH–]=1·10–14/0,2 = 5·10–14 моль/л.
2) Рассчитать концентрацию, моль/л, ионов [H+] и [OH–] в 0,1 М растворе гидроксида калия.
Решение: KOH ® K+ + OH–
Из уравнения реакции видно, концентрация ионов OH– равна концентрации щелочи, т.е. С(OH–) = С(КОН) = 0,1 моль/л.
Концентрацию ионов H+ рассчитаем из ионного произведения воды:
Kw = [H+][OH–] = 1·10–14: [H+]=1·10–14/0,1 = 1·10–13 моль/л.
Как видно из приведенных примеров, концентрация ионов H+ и OH– может меняться в очень широких пределах. По этой причине в расчетах удобнее использовать не концентрации, а их логарифмы (lg).
Прологарифмировав уравнение (6.4.2), получим:
lgKw = lg[H+] + lg[OH–] = –14
Умножим левую и правую части полученного уравнения на (–1):
–lgKw = – lg[H+] – lg[OH–] = 14
Математическое действие «– lg» обозначим значком «p», и в результате получим логарифмическую форму ионного произведения воды:
| pKw = pH + pOH = 14 | (6.3.3) |
В уравнении (6.3.3) pH – отрицательный десятичный логарифм молярной концентрации ионов водорода:
| pH = – lg[H+] | (6.3.4) |
pOH – отрицательный десятичный логарифм молярной концентрации гидроксид-ионов водорода:
| pOH = – lg[OH–] | (6.3.5) |
pKw – отрицательный десятичный логарифм ионного произведения воды:
pKw = – lgKw
В чистой воде
[H+] = [OH–], поэтому – lg[H+] = – lg[OH–] и соответственно
pH = pOH = pKw/2 = 14/2 = 7
В растворах кислот [H+] > [OH–], поэтому pH <7, pOH > 7.
В растворах оснований [H+] < [OH–], поэтому pH >7, pOH < 7.
Пример1
Рассчитать pH и pOH в 0,15 М растворах:
а) серной кислоты
Решение: H2SO4 ® 2H+ + SO42–
C(H+) = 2C(H2SO4) = 0,15·2 = 0,3 моль/л; pH = – lgС(H+) = 0,3 = 0,52;
pOH = 14 – 0,52 = 13,48.
б) 0,15 М гидроксида калия
Решение: KOH® K+ + OH–
С(OH–) = С(KOH) = 0,15; pOH = 0,82; pH = 14 – 0,82 = 13,18.
Диссоциация слабых одноосновных кислот и однокислотных оснований
HA « H+ + A– 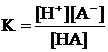
Пример 2
Рассчитать равновесную концентрацию ионов и недиссоциированных молекул в растворе кислоты концентрации С(HA), моль/л,имеющей константу диссоциации К.
Решение: из уравнения диссоциации видно, что
[H+] = [A], и [HA] = С(HA) – Сдис.(HA) = С(HA) – [H+].
Тогда выражение константы преобразуется в следующее: 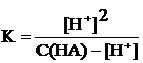 или [H+]2 + K[H+] – KC(HA) = 0
или [H+]2 + K[H+] – KC(HA) = 0
Решая это уравнение, определим [H+], [A–] и [HA], моль/л.
Довольно часто полученное расчетное уравнение можно упростить: если электролит очень слабый, то [H+] << С(HA), и величиной [H+] в знаменателе можно пренебречь. Тогда получим: 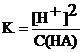 , откуда
, откуда
[H+] = [A–]= 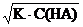 | (6.3.6) |
Эти уравнения применимы для расчетов в тех случаях, когда 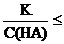 10–2.
10–2.
Пример 3
Рассчитать концентрацию продуктов диссоциации и pH в 0,15 М растворе кислоты, имеющей константу диссоциации Ка = 5·10–7.
Решение: HA « H+ + A– 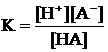 = 5·10–7
= 5·10–7
Проверим, выполняется ли условие 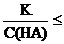 10–2:
10–2:
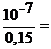 6,6·10–7 < 10–2, т.е. условие выполняется, и расчет можно вести по упрощенным формулам:
6,6·10–7 < 10–2, т.е. условие выполняется, и расчет можно вести по упрощенным формулам: 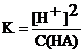 ,
,
[H+] = [A–] =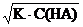 =
= 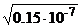 =1,07·10–4 моль/л
=1,07·10–4 моль/л
pH = – lg[H+] = – lg(1,07·10–4) = – lg1,07 – lg10–4 = 3,97.
Пример 4
Рассчитать концентрацию продуктов диссоциации и pH в 0,15 М растворе основания (KatOH), имеющего константу диссоциации Кb = 3·10–9.
Решение: KatOH « Kat+ + OH– 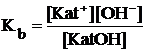 = 3·10–9
= 3·10–9
Проверим, выполняется ли условие 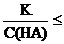 10–2:
10–2:
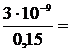 2×10–8 < 10–2, т.е. условие выполняется, и расчет можно вести по упрощенным формулам:
2×10–8 < 10–2, т.е. условие выполняется, и расчет можно вести по упрощенным формулам: 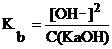 и
и
[Kat+] = [OH–] =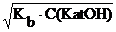 =
= 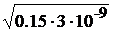 =2,12·10–5 моль/л
=2,12·10–5 моль/л
pOH = – lg[OH–] = – lg(2,12·10–5) = 4,68
pH = 14 – pOH = 14 – 3,68 = 10,32.
6.5 Диссоциация слабых многоосновных кислот
Пример
Рассчитать концентрации продуктов диссоциации в 0,1 М растворе фосфорной кислоты (K1 = 7,5·10–3, K2 = 6,3·10–8, K3 = 1,3·10–12).
Уравнения диссоциации:
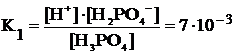
H3PO4 « H+ + H2PO4–
H2PO4– « H+ + HPO42–
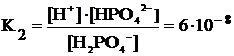
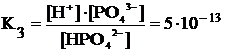
HPO42– « H+ + PO43–
Как следует из уравнений диссоциации, в растворе имеются недиссоциированные молекулы H3PO4, а также ионы (в порядке уменьшения их концентраций): H+, H2PO4–, HPO42–, PO43–.
Полный расчет материального баланса для сопряженных равновесий довольно сложен. В то же время для практических задач его часто можно упростить. Дело в том, что если константы ступенчатой диссоциации различаются на 4 порядка и более (что в нашем примере выполняется), то концентрацию ионов H+ можно рассчитывать с учетом только первой ступени диссоциации, как для одноосновной кислоты (см. пример 2). На том же основании можно не учитывать уменьшение концентрации ионов H2PO4– за счет их диссоциации по второй ступени, т.е. можно принять, что [H+] » [H2PO4–]. На основании этого получим исходное расчетное уравнение для первой ступени диссоциации:
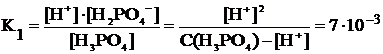
В отличие от примера, рассмотренного ранее, в данном случае не выполняется условие 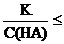 10–2, и поэтому необходимо решать полное квадратное уравнение, выведенное из константы равновесия:
10–2, и поэтому необходимо решать полное квадратное уравнение, выведенное из константы равновесия:
[H+]2 + K×[H+] – K×C(HA) = [H+]2 + 7,5·10–3·[H+] – 7,5·10–4 = 0, откуда
[H+] = [H2PO4–] = 0,024 моль/л.
Подставим полученные величины в константу диссоциации по второй ступени:
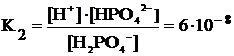
В числителе и знаменателе дроби оказались равные величины
[H+] = [H2PO4–], из чего следует, что [HPO42–] = K2 = 6·10–8 моль/л.
Таким образом, равновесная молярная концентрация двухзарядных анионов слабой многоосновной кислоты равна второй константе диссоциации.
Еще раз подчеркнем, что последний вывод справедлив при условии, что константы ступенчатой диссоциации различаются не менее чем на четыре порядка (для большинства неорганических кислот – сернистой, сероводородной, угольной и др. – это условие выполняется).
Наконец, из константы диссоциации по третьей ступени рассчитаем равновесную молярную концентрацию фосфат-ионов:
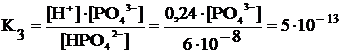
[PO43–] = 5·10-13·6·10–8/0,024 = 1,25·10–18 моль/л.
6.6 Степень диссоциации слабых электролитов
Степень диссоциации (α) показывает, какая часть электролита продиссоциировала:
| α = Nдис./Nнач. = nдис./nнач. = Сдис./Снач. | (6.4.1) |
Для расчета степени диссоциации слабой кислоты HA « H+ + A–
в растворе с концентрацией Снач = С(HA) можем записать, что Сдис = α ∙ С(HA).
Учитывая, что Сдис. = [H+] = [A–], получим: Сдис. = [H+] = [A–] = α∙ С(HA).
Подставив эти обозначения в выражение константы диссоциации, получим следующее уравнение для расчета степени диссоциации:
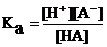 =
= 
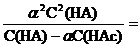
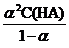 .
.
Если α << 1, то в полученном уравнении можно считать, что (1 – α) » 1;
тогда Ka = α2С(HA), и
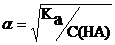 | (6.4.2) |
Таким образом, степень диссоциации слабого электролита обратно пропорциональна корню квадратному из его концентрации. Зависимость (6.4.2)была выведена Оствальдом и носит его имя – закон разбавления Оствальда.
Закон разбавления можно вывести также из ранее полученного уравнения [H+] = 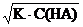 , подставив в него [H+] = α∙C(HA), получим то же уравнение (6.4.2):
, подставив в него [H+] = α∙C(HA), получим то же уравнение (6.4.2):
α = 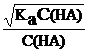 =
= 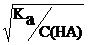
Аналогичные уравнения можно вывести для степени диссоциации слабого основания. Отличие будет только в том, что вместо константы диссоциации кислоты (Ка) в уравнении будет константа основания (Kb). Еще раз отметим, что упрощенный расчет допустим при условии, что α << 1 (при 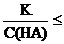 10–2); при невыполнении этого условия решается полное квадратное уравнение.
10–2); при невыполнении этого условия решается полное квадратное уравнение.
6.7 Смещение равновесий диссоциации слабых электролитов (влияние одноименных ионов на диссоциацию)
В соответствии с принципом Ле Шателье равновесие диссоциации слабой кислоты HA « H+ + A– можно изменить, если изменить температуру или концентрации веществ, участвующих в равновесии.
Диссоциация – процесс эндотермический, поэтому при увеличении температуры равновесие сместится вправо (степень диссоциации и концентрация ионов в растворе увеличивается); при охлаждении раствора равновесие сместится в обратном направлении.
При увеличении концентрации кислоты равновесие сместится в прямом направлении (концентрация ионов в растворе увеличится, но степень диссоциации уменьшится – см. закон разбавления Оствальда).
Если в раствор добавить сильную кислоту, увеличив тем самым концентрацию ионов H+, то равновесие сместится влево (степень диссоциации и концентрация анионов A– уменьшатся, но концентрация ионов H+ будет большей, чем до добавления сильной кислоты).
Если в раствор добавить растворимую соль слабой кислоты (KatA), увеличив тем самым концентрацию анионов A–, то равновесие сместится в сторону их связывания, т.е. влево (степень диссоциации и концентрация ионов H+ уменьшатся, а концентрация анионов A– будет больше, чем до прибавления соли).
Пример 1. В 0,1 М раствор кислоты, имеющей константу диссоциации Ка = 2·10–7, добавили соляную кислоту, С(HCl) = 0,5 моль/л. Рассчитать степень диссоциации слабой кислоты в полученном растворе и его pH.
Решение: HA « H+ + A– HCl ® H+ + Cl–
1) После добавления сильной кислоты диссоциация слабой кислоты будет подавлена, и концентрацией ее «собственных» ионов водорода можно пренебречь, считая, что в полученном растворе С(H+) = С(HCl) = 0,5 моль/л.
Тогда pH = – lg С(H+) = – lg 0,5 = 0,3.
2) Вследствие того, что ионы водорода в растворе, в основном, из соляной кислоты, их концентрация теперь не может быть показателем степени диссоциации слабой кислоты – это отражает только концентрация ее анионов A–. Последнюю можно рассчитать через константу диссоциации, с учетом того, что [H+] = С(HCl) и [HA] » С(HA):
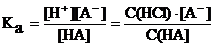 = 2·10–7 [A–] = 2·10-7·0,1/0,5 = 4·10–8 моль/л
= 2·10–7 [A–] = 2·10-7·0,1/0,5 = 4·10–8 моль/л
Тогда степень диссоциации кислоты α = [A–]/С(HA) = 4·10–8/0,1 = 4·10–7.
6.8 Буферные растворы
«Буферными» называют системы и устройства, смягчающие внешние воздействия на систему, устройства и т.д. Вспомните буферные устройства между железнодорожными вагонами; бамперы автомобилей – те же буферы; «буферные зоны» при международных конфликтах и т. д.
Буферными называют растворы, при добавлении к которым кислот или щелочей их pH меняется незначительно. Механизм буферного действия основан на том, что в состав раствора входят анионы слабых кислот или (и) катионы слабых оснований, способные превращать сильные кислоты или основания в слабые. В соответствии с изложенным выше буферными свойствами обладают:
а) растворы, содержащие слабые кислоты (HA) и их соли (KatA) – кислотные буферные растворы: HA « H+ + A– KatA ® Kat+ + A–
Если в такой раствор добавить, например, соляную кислоту
HCl ® H+ + Cl–, то ее ионы водорода будут связывать анионы соли, образуя слабую кислоту (HA): H+ + A–®HA.
Если в раствор добавить, например, гидроксид натрия NaOH ® Na+ + OH–, то гидроксид-ионы свяжутся ионами водорода кислоты, образуя воду: HA + OH– « H2O + A–
б)растворы, содержащие слабые основаня (KatOH) и их соли (KatA) – основные буферные растворы:
KatOH « Kat+ + OH– KatA ® Kat+ + A–
Если в такой раствор добавить, например соляную кислоту
HCl ® H+ + Cl–, то ее ионы водорода будут связывать гидроксид-ионы основания, образуя воду: KatOH+H+ «H2O+Kat+
Если в раствор добавить, например гидроксид натрия
NaOH ® Na+ + OH–, то его гидроксид-ионы свяжут катионы соли, образуя слабое основание: Kat+ +OH–®KatOH
в) растворы кислых солей слабых кислот (гидрокарбонаты, гидрофосфаты и др.), а также растворы аминокислот.
Буферные свойства кислых солей обусловлены тем, что их анионы в кислотно-основных реакциях могут выполнять двойную функцию: за счет имеющихся ионов водорода нейтрализовать щелочь или связывать ионы водорода с образованием слабых кислот.
Например, в растворе гидрофосфата натрия протекают следующие реакции электролитической диссоциации:
Na2HPO4 ® 2Na+ + HPO42–, HPO42– « H+ + PO43–
Если в такой раствор добавить, например, соляную кислоту
HCl ® H+ + Cl–, то ее ионы водорода будут связывать фосфат-ионы, образуя слабые кислоты (гидрофосфат-ионы или молекулы фосфорной кислоты):
PO43–+H+ «HPO42–, HPO42– + H+ «H2PO4–, H2PO4– + H+ «H3PO4
Если в раствор добавить щелочь, например NaOH: NaOH ® Na+ + OH–, то гидроксид-ионы свяжутся с гидрофосфат-ионами соли, образуя воду:
HPO42– + OH– «PO43– + H2O
Расчет pH буферных растворов
а) кислотные буферные растворы.
Как отмечалось выше, в их состав входят слабые кислоты и их соли:
HA « H+ + A– KatA ® Kat+ + A–
Напишем выражение константы диссоциации кислоты:
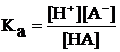
С учетом того, что кислота слабая, к тому же ее диссоциация подавлена в присутствии одноименных анионов ее соли, можно считать, что [HA] = С(HA) и [A–] = Ссоли. Тогда выражение константы преобразуется в следующее:
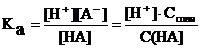 , откуда
, откуда
[H+] = Ka  | (6.8.1) |
Соответственно pH такого раствора:
pH = – lg[H+] = pKa + pС(HA) – pСсоли
Пример. Рассчитать pH раствора при С(HF) = 0,2 M и С(KF) = 0,1 M.
Решение: буфер кислотный, следовательно
[H+] = Ka  ; [H+] = KHF
; [H+] = KHF 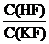 = 6
= 6 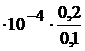 = 1,2
= 1,2 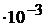 M, тогда pH = 2,92.
M, тогда pH = 2,92.
б) основные буферные растворы.
В их состав входят слабые основания и их соли:
KatOH « Kat+ + OH– KatA ® Kat+ + A–
Напишем выражение константы диссоциации слабого основания:
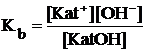
С учетом того, что основание слабое, к тому же его диссоциация подавлена в присутствии одноименных анионов его соли, можно считать, что [KatOH] = С(KatOH) и [Kat+] = Ссоли. Тогда выражение константы преобразуется в следующее:
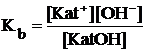 =
= 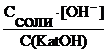 , откуда
, откуда
[OH–] = 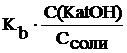 , , | (6.8.2) |
тогда pOH = – lg[OH–] = pKb + pC(KatOH) – pCсоли
pH = 14 – pOH = 14 – pKb – pC(KatOH) + pCсоли
Пример. Рассчитать pH буферного раствора, состоящего из аммиака с молярностью 0,2 М и хлорида аммония, С(NH4Cl) = 0,2 M.
Решение
Для основного буфера:
[OH–] = 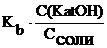 =
= 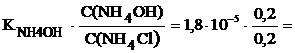 =1,8
=1,8  , тогда pOH = 4,74; pH = 10,26.
, тогда pOH = 4,74; pH = 10,26.
Из формул (6.8.1) и (6.8.2) следует еще одно свойство буферных растворов: их кислотность не меняется при разбавлении. Действительно, при разбавлении растворов концентрации веществ, входящих в числитель и знаменатель дроби в выражениях (6.8.1) и (6.8.2), меняются в равное число раз.
Гидролиз солей
Гидролиз – это частный случай обменных реакций, в которых реальные или потенциальные ионы растворенного вещества заменяются на ионы воды.
Обменные реакции, в которых в которых составные части растворенного вещества связываются с ионами воды, образуя слабые кислоты и (или) слабые основания, называют реакциями гидролиза.
Как и другие реакции обмена, гидролиз возможен в случае, если его продуктами оказываются слабые электролиты (или неэлектролиты), а также малорастворимые продукты (твердые или газообразные).
Гидролизу подвергаются многие вещества, как органические, так и неорганические: соли, галогенангидриды, эфиры, жиры и др.
При растворении солей в воде большинство их под влиянием молекул растворителя полностью диссоциируют на катионы и анионы:
KatxAy 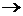 xKaty+ + yAx–
xKaty+ + yAx–
Вода – один из слабейших неорганических электролитов – хотя и в малой степени, но также диссоциирует на ионы, при этом одновременно с реакцией диссоциации протекает обратная реакция – ассоциация ионов H+ и OH– с образованием молекул воды:
HOH 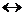 H+ + OH–
H+ + OH–
В чистой воде молярные концентрации ее ионов одинаковы, поэтому pH = 7 (см. тему «Диссоциация электролитов»). Если в растворе появляются ионы соли, то баланс между ионами H+ и OH– может нарушиться. Так, если катионам соли соответствует слабое основание, то они могут конкурировать с ионами водорода за связывание гидроксид-ионов, в результате чего ионы H+ окажутся в избытке, и раствор будет подкисляться:
Katy+ + H–OH 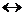 (Kat–OH)(y–1)+ + H+
(Kat–OH)(y–1)+ + H+
Если анионам соли соответствует слабая кислота, то они могут конкурировать с гидроксид-ионами за связывание ионов водорода, в результате чего ионы OH– окажутся в избытке, раствор будет подщелачиваться:
Ax– + H–OH 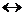 (H–A)(x–1)– + OH–
(H–A)(x–1)– + OH–
Таким образом, из солей гидролизуются те, в состав которых входят катионы слабого основания и (или) анионы слабой кислоты. Чем слабее электролит, образующийся при гидролизе, тем более полно протекает гидролиз.
Если заряды (x, y) гидролизующихся ионов соли больше единицы, то такие реакции протекают в несколько стадий (ступеней).
Например, катионы алюминия, связывая гидроксид-ионы воды, могут образовать гидроксоалюминат-, дигидроксоалюминат-катионы и молекулы гидроксида:
Al3+ + HOH 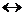 AlOH2+ + H+ – первая ступень;
AlOH2+ + H+ – первая ступень;
AlOH2+ + HOH 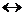 Al(OH)2+ + H+ – вторая ступень;
Al(OH)2+ + H+ – вторая ступень;
Al(OH)2+ + HOH 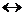 Al(OH)3 + H+ – третья ступень.
Al(OH)3 + H+ – третья ступень.
Сульфид-ионы могут связывать ионы водорода, образуя гидросульфид- ионы и молекулы сероводорода:
S2– + HOH 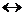 HS– + OH– – первая ступень;
HS– + OH– – первая ступень;
HS– + HOH 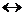 H2S + OH– – вторая ступень.
H2S + OH– – вторая ступень.
Уравнения реакций гидролиза
При написании ионных и молекулярных реакций гидролиза рекомендуется следующая последовательность их составления:
а) написать уравнение диссоциации соли и выделить ионы, способные участвовать в гидролизе;
б) написать уравнение реакции этих ионов с молекулами воды (сокращенное ионно-молекулярное уравнение гидролиза);
в) добавить в уравнение (б) ионы соли, не участвующие в гидролизе (получится полное ионно-молекулярное уравнение);
г) соединить катионы и анионы в левой и правой частях уравнения (в) с образованием соответствующих электролитов (получится молекулярное уравнение гидролиза).
Примеры
Гидролиз солей слабых оснований:
– соли, образованные однозарядным катионом слабого основания:
NH4NO3 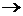 NH4+ + NO3– – уравнение диссоциации
NH4+ + NO3– – уравнение диссоциации
(выделены ионы слабого основания, NH4+);
NH4+ + HOH 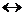 NH3·H2O + H+ – сокращенное ионно-молекулярное уравнение, из которого видно, что раствор кислый, его pH < 7;
NH3·H2O + H+ – сокращенное ионно-молекулярное уравнение, из которого видно, что раствор кислый, его pH < 7;
NH4+ + NO3– + HOH 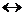 NH3·H2O + H+ + NO3– – полное ионно-молекулярное уравнение (в левую и правую части добавили NO3–);
NH3·H2O + H+ + NO3– – полное ионно-молекулярное уравнение (в левую и правую части добавили NO3–);
NH4NO3 + H2O  NH3·H2O + HNO3– молекулярное уравнение гидролиза.
NH3·H2O + HNO3– молекулярное уравнение гидролиза.
– соли, образованные многозарядным катионом слабого основания и однозарядным анионом сильной кислоты (CuCl
