Расчет материального баланса в состоянии химического равновесия

Для любой равновесной системы, например 2A « 3D + B, расчет материального баланса можно сделать только с применением константы равновесия: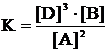

Для любой равновесной системы делается баланс по каждому реагенту с учетом начального его количества, прореагировавшего количества и остатка, участвующего в равновесии. Например, для приведенной выше реакции баланс по веществу Аможно записать так: С_нач.(А) = С_р.(А) + [A],

где C_р.(А) – концентрация вещества А прореагировавшего и [A] – его равновесная концентрация.

Веществ BиD – продуктов, до реакции не было, поэтому для них

С_нач.(B) = 0 и С_нач.(D) = 0.

Зная, сколько прореагировало исходного вещества А,можно с помощью уравнения реакции (по соотношению коэффициентов) определить равновесные концентрации продуктов веществ B и D: по уравнению реакции из 2 моль вещества А образуются 1 моль вещества В, поэтому, если прореагировало C_р.(А), то образуется вдвое меньше вещества В, т.е. [B] = 0,5С_р.(А); далее, из 2 моль вещества А образуется 3/2 моль вещества D, тогда [D] = 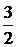С_р.(А).

Если вещества А прореагировало С_р.(А), то его осталось и участвует в равновесии С_нач.(А) – С_р.(А) = [A].

Различные варианты расчетов материального баланса рассмотрим далее на примере равновесия 2NO + Cl₂ « 2NOCl.

Пример 1. По равновесным концентрациям реагентов, равным:

[NO] = 2 моль/л, [Cl₂] = 1 моль/л, [NOCl] = 2 моль/л рассчитать начальные концентрации реагентов и константу равновесия.

Решение: на начало реакции продукта NOCl не было, поэтому С_нач.(NOCl) = 0.

Из уравнения реакции видно, что для образования 2 моль/л NOCl должно прореагировать столько же NO (коэффициенты в уравнении одинаковые).

Следовательно, прореагировало NO: С_р(NO) = [NOCl] = 2 моль/л.

Тогда начальная концентрация NO:

С_нач.(NO) = [NO] + С_р(NO) = 2 + 2 = 4 моль/л.

Расчет прореагировавшего Cl₂ можно сделать уже двумя вариантами: либо через NOCl (см. выше), либо по прореагировавшему NO:

Из уравнения видно, что если в реакцию вступило С_р(NO), то с ним прореагировало в два раза меньше Cl₂, т.е. С_р(Cl₂) = 0,5С_р(NO) = 0,5·2 = 1 моль/л.

Тогда начальная концентрация Cl₂:

С_нач.(Cl₂) = [Cl₂] + С_р(Cl₂) = 1 + 1 = 2 моль/л.

Рассчитаем константу равновесия: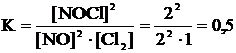

Пример 2. По заданным начальным концентрациям С_нач.(Cl₂) = 2 моль/л, С_нач.(NO) = 2 моль/л и К = 0,5 рассчитать равновесные концентрации [NO], [Cl₂] и [NOCl] и степень протекания реакции по NO.

Решение: 2NO + Cl₂ « 2NOCl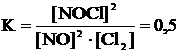

Решение данной задачи сводится к тому, чтобы в уравнении константы

равновесия вместо трех неизвестных иметь одно и через него выразить остальные.

Обозначим [NO] = x, и рассчитаем концентрацию прореагировавшего NO: С_р(NO) = С_нач.(NO) – [NO] = С_нач.(NO) – x = 2 – x

Из уравнения реакции видно, что, сколько прореагирует NO, столько же получится NOCl, и это его равновесная концентрация, т.е. [NOCl] = 2 – x

Из уравнения реакции видно, что хлора прореагирует в 2 раза меньше, чем NO, т.е. С_р(Cl₂) = 0,5С_р(NO) = 0,5(2 – x) = 1 – 0,5x.

Тогда [Cl₂] = 2 – (1 – 0,5x) = 1 + 0,5x

Из константы равновесия рассчитаем [NO] = x:

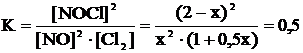; откуда x = 1,1 моль/л

Таким образом:

[NO] = 1,1 моль/л, [Cl₂] = 1 + 0,5x = 1,55 моль/л,

[NOCl] = 2 – x = 0,9 моль/л

Степень протекания реакции по NO:

α = С_р(NO)/С_нач.(NO) = (С_нач.(NO) – [NO])/С_нач.(NO) = (2 – 1,1)/2 = 0,45

α = 0,45 или 45 %.

Основы химической кинетики

Химическая кинетика – учение о химическом процессе, его механизме и закономерностях протекания во времени.

Химическая кинетика наряду с химической термодинамикой – теоретическая основа химической технологии, поскольку позволяет оптимизировать и интенсифицировать промышленно важные реакции. Тепловой эффект реакции, преимущественное направление и глубина ее протекания определяются законами термодинамики; однако из них совсем не следует возможность прогнозирования скорости перехода из начального в конечное состояние, а также через какие промежуточные стадии проходит это превращение.

Пример: H_2(г) + 1/2O_2(г) ® H₂O(г) H⁰ = – 242 кДж/моль

NO_(г) + 1/2O_2(г) ® NO_2(г) H⁰ = – 56 кДж/моль

Первая реакция энергетически более выгодна, однако скорость ее несравнимо меньше, чем второй реакции.

Основные понятия и определения

Механизм химической реакции – совокупность элементарных стадий, из которых складывается химическая реакция.

Элементарной называют реакцию, которая осуществляется превращением реагентов в продукты реакции в одну стадию.

Молекулярность реакции – число частиц (молекул, атомов, радикалов, ионов), участвующих в элементарном акте химической реакции. Различают мономолекулярные реакции (в элементарном акте участвует одна молекула), например, реакции изомеризации или разложения:

2N₂O_5(г) = 4 NO_2(г) + O_2(г)

– бимолекулярные реакции, в которых две молекулы участвуют в образовании одного или нескольких веществ, например, реакции соединения или обмена (А + B = С, AB + CD = AD + BC): C₂H₄ + HI = C₂H₅I

– тримолекулярные реакции, которые протекают при одновременном столкновении трех молекул (встречаются довольно редко):

2NO + Cl₂ = 2NOCl

Реакции более чем тримолекулярные практически не встречаются.

Скорость химической реакции – это число элементарных актов химического взаимодействия, протекающих в единицу времени в единице объема (для гомогенных реакций) или на единице поверхности (для гетерогенных реакций) – это абсолютная скорость. Для реакций, даже очень медленных, абсолютная скорость огромна. Например, если

А

из одного моля вещества за секунду реагирует 1/1000000000 часть молекул, то это

В

составляет (вспомните число Авогадро) ~ 10¹⁵ молекул. Поэтому на практике определяют не абсолютную скорость реакции, а ее результат – изменение количества или концентрации вещества за единицу времени. При этом различают мгновенную и среднюю скорости реакции.

Мгновенная скорость – это скорость на определенное время (короткое мгновение): V = ± dС/dt

(если скорость контролируется по образующемуся продукту, то знак «+», если по расходу исходного реагента, то «–»)

Среднюю скорость определяют по изменению количества ( n) или концентрации ( C) вещества за определенный временной интервал ( t):

Vср. = ± С/ t

По результатам измерений концентраций во времени строят так называемые кинетические кривые. Например, в ходе реакции А®В концентрация реагента А уменьшается, а реагента В – увеличивается (рисунок 4.4.1).

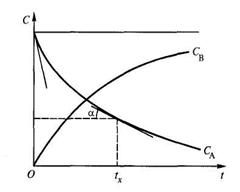
Рисунок 4.4.1 –Типичные кинетические кривые для исходного вещества А и продукта реакции В

С помощью кинетической кривой можно графически определить мгновенную скорость, в момент времени t_х: для этого потребуется восстановить перпендикуляр от оси абсцисс в т. t_x до пересечения его с кинетической кривой и провести касательную к точке пересечения. Тангенс угла наклона касательной и есть мгновенная скорость (V = dс/dt).

Влияние концентраций реагирующих веществ на скорость химической реакции. Закон действующих масс

Зависимость скорости реакции от концентрации реагирующих веществ показывает кинетическое уравнение (уравнение кинетической кривой).

Например, для условной реакции aA + bB ® dD + fF кинетическое уравнение можно представить в следующем виде:

V = kСx(A)Сy(B)

(4.4.1)

Уравнение (4.4.1) часто называют законом действующих масс, который для элементарных реакций сформулировали К.Гульдберг и П.Вааге.

Коэффициент k, входящий в уравнение (4.4.1), называют константой скорости реакции. Константа скорости реакции зависит от природы реагирующих веществ и температуры. Поскольку k = V при С = 1 моль/л, то ее иногда называют удельной скоростью.

Обратите внимание на то, что в большинстве случаев стехиометрические коэффициенты в уравнении реакции не отражают истинного механизма реакции. По этой причине показатели степеней (x, y) при концентрациях в уравнении (4.4.1) очень редко соответствуют стехиометрическим коэффициентам (в отличие от закона действующих масс применительно к химическому равновесию).

Показатели степеней x, y при концентрациях реагентов А и В в уравнении (4.4.1) называют порядком реакции по веществу А и веществу В, соответственно, а сумму (x + y) называют общим порядком реакции.

Порядок химической реакции, как по отдельным реагентам, так и общий, определяют экспериментально. По этим данным составляют кинетические уравнения. В зависимости от суммы (x + y) различают реакции нулевого, первого, второго или третьего порядка. (Реакции более высоких порядков не встречаются; поэтому в случае, если сумма стехиометрических коэффициентов в уравнении реакции превышает три, то это заведомо многостадийная реакция).

Скорость большей части реакций описывается кинетическим уравнением первого порядка: dС/dt = kt или в интегральной форме:

С = С0exp(–kt)

(4.4.2)

Если интересен расчет не концентрации на определенное время t, а изменение концентрации, то уравнение (4.4.2) преобразуют в более удобное:

ln(С0/С) = kt

(4.4.3)

Время полуреакции (t½) – это время, за которое количество вещества (или число его частиц, или масса, или его молярная концентрация) уменьшается вдвое. Из уравнения (5) легко вывести, что при с₀/c = 2

t½ = ln2/k = 0,693/k

(4.4.4)

Определение времени полуреакции – это один из способов определения порядка реакции: если реакция протекает наполовину за время, соответствующее уравнению (4.4.4), то это реакция первого порядка (другие варианты определения порядка реакции будут рассмотрены при изучении физической химии).

К числу реакций первого порядка относятся и реакции радиоактивного распада. Для них время полуреакции обычно называют периодом полураспада. Это время, за которое распадается половина вещества (по химическому количеству, массе или активности). Периоды полураспада (t½) различных радиоизотопов приведены в справочниках. Зная t½, по уравнению (4.4.4), легко рассчитать константу скорости распада, а затем по уравнениям (4.4.2) или (4.4.3) – изменение количества вещества или его активности (А):

A = A0 ∙exp(– k∙t),

(4.4.5)

где А₀ – это начальная активность вещества, А – активность на время t.

За единицу «активности» традиционно принимают 1Кюри = = 3,8×10¹⁰ распадов/с; в СИ активность измеряют в Беккерелях (Бк): 1 Ku = = 3,37×10¹⁰ Бк.

Пример: период полураспада изотопа ¹⁴С равен 5730 лет. При археологических раскопках нашли дерево, в котором содержание ¹⁴С составило 56 % от нормального. Каков возраст дерева (с)?

Решение

Поскольку в условии дано соотношение масс углерода, то кинетическое уравнение удобнее выразить через массы веществ:

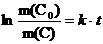
1) Рассчитаем k = ln2/t½ = 3,8×10^–12

2) Рассчитаем t = ln(1/0,56)/3,8×10^–12 = 1,52×10¹¹

Ответ: с = 4800 лет.

Влияние температуры на скорость химической реакции. Уравнение Аррениуса

Согласно эмпирическому правилу Вант-Гоффа, скорость большинства химических реакций увеличивается в 2÷4 раза при повышении температуры на каждые 10 градусов:

V_T2/V_T1 = γ^(T+10)/T, где γ = 2÷4 – температурный коэффициент реакции.

Довольно часто, особенно в учебной литературе по химии для средней школы, влияние температуры на скорость химической реакции объясняют тем, что при увеличении температуры увеличивается скорость движения частиц, вследствие этого увеличивается вероятность их столкновения и вероятность реакции между ними. Вроде бы логично.

Однако из молекулярно-кинетической теории газов известно, что средняя скорость движения молекул пропорциональна корню квадратному из абсолютной температуры. Так, если температуру увеличить с T₁ = 298 K до T₂ = = 398 K, то увеличение средней скорости движения молекул составит:

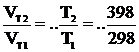= 1,15, т.е. всего 15 %.

Если реакция между этими молекулами характеризуется температурным коэффициентом γ = 2, то при том же увеличении температуры на 100 градусов скорость реакции должна увеличиться: V₃₉₈/V₂₉₈ = 2¹⁰ = 1024 раза.

Как видно, при увеличении температуры скорость реакции увеличилась многократно больше по сравнению с увеличением скорости движения молекул. Из этого следует очевидный вывод: увеличение скорости движения молекул – не единственная и совсем не основная причина увеличения скорости реакции; здесь действует еще какой-то важный фактор.

Зависимость скорости реакции от природы реагирующих частиц. Понятие об активных частицах, активных соударениях и энергии активации

В приведенных выше расчетах сравнивались средние скорости теплового движения молекул в зависимости от температуры. В то же время, если число частиц велико, то по законам статистики реальное распределение частиц по скоростям в зависимости от температуры будет другим (рисунок 4.4.2).

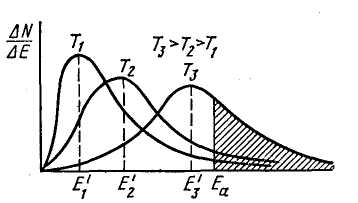
Рисунок 4.4.2 – Распределение частиц по кинетической энергии при различных температурах: 1 – при Т₁, 2 – при Т₂, 3 – прим Т₃; Т₁ < Т₂ < Т₃; Е₁ – наиболее вероятная энергия при температуре Т₁

В молекулярно-кинетической теории газов распределение частиц по энергии в зависимости от температуры описывается уравнением Больцмана: N = N₀exp(–Ea/RT), где N – число частиц с энергией, равной и большей, чем Еа.

Общее число частиц в системе (N₀) равно площади под кривой. При температуре Т₁ максимальной энергией Е₁ обладают N₁ частиц. Общее число частиц с энергией меньше, чем Е₁, равно площади левее от вертикали Е₁, а частиц с энергией большей, чем Е₁ – правее этой вертикали.

Из рисунка 4.4.2 видно, что при увеличении температуры распределение частиц по энергии меняется так, что увеличивается доля частиц с большей энергией (кривая распределения смещается вправо, в область больших Е).

Если для химического взаимодействия частиц необходимо, чтобы они имели энергию Е_аи более, то из рисунке 4.4.2 видно, что при температуре Т₁ доля таких частиц незначительна, а при температуре Т₃ таких частиц примерно 30 %.

В 1889 г. С.Аррениус показал, что уравнением, аналогичным (4.4.5), можно связать с абсолютной температурой константу скорости химической реакции:

k = A∙exp(– Ea/RT)

(4.4.6)

Из уравнения Аррениуса следует, что скорость реакции определяется не общим числом столкновений частиц, а только столкновением частиц с энергией, равной и превышающей Е_а.

Почему не всякое столкновение ведет к химической реакции? Для ответа на этот вопрос вспомним, что образование новых химических связей – результат перераспределения электронной плотности между атомами, а для этого необходимо перекрывание электронных (одноименно заряженных) оболочек. Чем более «жестки» электронные оболочки сталкивающихся частиц, тем больший энергетический барьер потребуется преодолеть частицам для химического взаимодействия. Именно по этой причине при низких температурах малы скорости реакций с участием молекулярных кислорода и азота.

Кроме того, в химических реакциях, например, в растворах электролитов, в реакциях могут участвовать ионы, в том числе и одноименно заряженные. С рассмотренных выше позиций становится понятным, почему реакции ионного обмена с участием противоположно заряженных частиц протекают практически мгновенно, а окислительно-восстановительная реакция между анионами MnO₄^– и C₂O₄^2– без нагревания идет очень медленно.

Энергию, которой должны обладать частицы при столкновении, чтобы оно привело к химической реакции, называют энергией активации (Е_а в уравнении (4.4.6).

Частицы, обладающие такой энергией, называют активными. Зависимость скорости химической реакции от природы реагирующих частиц отражается через величину энергии активации: чем меньше энергия активации, тем больше константа и тем больше скорость реакции. Для реакций, протекающих с заметной скоростью, энергия активации не превышает 50 кДж/моль (для реакций ионного обмена E_a » 0); если E_a > 100 кДж/моль, то скорость реакции неизмеримо мала.

Увеличение числа активных частиц при повышении температуры иявляется основной причиной увеличения скорости химической реакции. Количественно эту зависимость можно вывести из уравнения Аррениуса:

ln(kT2/kT1) = Ea(1/T1 – 1/T2)/R

(4.4.7)

Катализ. Понятие об активированном комплексе

Катализ – это ускорение химической реакции за счет введенного дополнительно вещества – катализатора, которое по окончании реакции остается в исходном состоянии и количестве.

Если уравнения (4.4.1) и (4.4.6) объединить в одно, то получим уравнение, отражающее зависимость скорости реакции от всех факторов:

V = A×exp(– Ea/RT)Cx(A)Cy(B)

(4.4.8)

– от природы реагирующих веществ – через E_a;

– от концентрации реагирующих веществ;

– от температуры.

За счет чего катализатор может изменить (иногда – в тысячи раз) скорость реакции? Если учесть, что его добавляют в очень незначительных количествах, по сравнению с основными реагентами, то, очевидно, что за счет изменения концентрации реагентов или их температуры катализатор не может влиять на скорость реакции. Остается один вариант – при введении катализатора уменьшается энергия активации.

Энергия активации зависит от природы реагирующих веществ, следовательно, катализатор изменяет путь реакции, ее промежуточные стадии, образуя какие-то новые промежуточные продукты с меньшей энергией активации (рисунок 4.4.3).

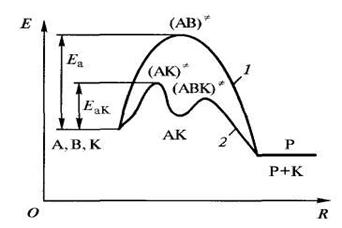
Рисунок 4.4.3 – Изменение пути химической реакции в присутствии катализатора: 1 – путь реакции без катализатора; 2 – путь реакции с атализатором; А, В – исходные вещества, К – катализатор, АК, АВК – «активированные комплексы», АК – промежуточный продукт, Р – конечный продукт.

Схему катализа можно представить следующим образом: если без катализатора продукт D образуется из веществ А и В в соответствии с уравнением А + В = D, то при введении катализатора Кпуть реакции меняется:

A + B + K ® AK + B ® AKB ® D + K

Хорошо известен пример окисления сернистого ангидрида в серный, катализируемого оксидом азота(II). Без катализатора окисление SO₂ идет очень медленно (особенности молекулярного кислорода как окислителя обсуждались нами ранее).

При введении в реакционную смесь NO окисление протекает в две стадии: сначала кислородом окисляется NO: 2NO + O₂ = 2NO₂,

далее NO₂ реагирует с SO₂: NO₂ + SO₂ = SO₃ + NO

В примере NO₂ выполняет роль промежуточного продукта; на второй стадии реакции из него «регенерируется» в исходной форме катализатор NO.

Примечание: на самом деле первая реакция, образование NO₂, не одно-, а двустадийная. В ней участвуют не две изолированные молекулы NO, а димер:

2NO « N₂O₂,

далее димер окисляется молекулярным кислородом: N₂O₂ + O₂ = 2NO₂.

Таким образом, окисление NO молекулярным кислородом – не одностадийная тримолекулярная реакция, а комбинация двух последовательных бимолекулярных реакций. Без этого уточнения был бы необъясним известный факт, что скорость окисления NO кислородом уменьшается с увеличением температуры.

В качестве другого примера катализа, применяемого в промышленности, можно рассмотреть синтез ацетальдегида. Пример особо интересен тем, что процесс был сначала сконструирован «на кончике пера». Так, еще в 1894 г. было установлено, что этилен восстанавливает влажный PdCl₂ до металлического палладия, при этом среди продуктов обнаружили ацетальдегид:

PdCl2 + C2H4 + H2O = Pd + CH3CHO + 2HCl

(а)

С другой стороны, было известно, что металлический палладий окисляется катионами Cu²⁺:

2CuCl2 + Pd = 2CuCl + PdCl2

(б)

И, наконец, известно, что CuCl в кислых растворах легко окисляется кислородом:

2CuCl + 0,5O2 + 2HCl = 2CuCl2 + H2O

(в)

В результате (а) + (б) + (в) получили:

PdCl₂ + C₂H₄ + H₂O + 2HCl + 2CuCl₂ + 0,5O₂ =

= PdCl₂ + CH₃CHO + H₂O + 2HCl + 2CuCl₂

PdCl₂/CuCl₂

C₂H₄ + 0,5 O₂ —® CH₃CHO – изящный каталитический процесс

Сейчас эта реакция, «сконструированная» в МИТХТ им. М. В. Ломоносова, является лучшим промышленным способом получения ацетальдегида (Вакер–процесс).

Автокатализ – это ускорение химической реакции продуктами этой реакции. В качестве примера можно рассмотреть окисление оксалатов перманганат-ионами в кислой среде. С точки зрения кинетики протекание реакции на первый взгляд неожиданно: по мере расходования реагентов скорость реакции не уменьшается, а увеличивается (до определенной величины). Причина в том, что эта реакция катализируется ионами Mn²⁺ – одним из продуктов этой реакции:

2MnO₄^- + C₂O₄^2- + 8H⁺ = 2Mn²⁺ + 2CO₂ + 4H₂O

Если к раствору оксалата изначально добавить небольшое количество соли Mn²⁺, то скорость реакции будет заметно больше уже «со старта».

Окисление молекулярным кислородом гидроксидов некоторых d-металлов (Fe²⁺, Mn²⁺, Co²⁺ и др.) интересно тем, что эти гидроксиды сами катализируют собственное окисление.

Гомогенный и гетерогенный катализ различаются по фазовому состоянию реагентов и катализатора. Если катализатор образует единую фазу с реагентами, то это гомогенный катализ (см. выше примеры катализа окисления SO₂ в газовой фазе и оксалатов в водном растворе). Если катализ протекает на границе раздела фаз – то это гетерогенный катализ.

Важнейшей характеристикой катализатора является его селективность (избирательность). Это свойство катализатора ускорять не все реакции, а только определенные, в идеале – одну единственную. Такие варианты катализа чаще всего реализуются в живых системах с помощью так называемых биокатализаторов.