Закон Гесса: тепловой эффект реакции зависит только от состояния исходных веществ и продуктов реакции и не зависит от пути перехода (т.е. от числа промежуточных стадий).
Пример: Стандартная энтальпия образования серной кислоты по справочным данным равна  fH0 = – 814 кДж/моль и по определению
fH0 = – 814 кДж/моль и по определению  fH0 соответствует схеме превращения: H2(г) + S(кр) + 2O2(Г) = H2SO4.(ж).
fH0 соответствует схеме превращения: H2(г) + S(кр) + 2O2(Г) = H2SO4.(ж).
Практически синтез H2SO4. из простых веществ можно реализовать в несколько стадий:
H2(г) + ½O2(г) = H2O(ж)  H10 = – 286 кДж/моль
H10 = – 286 кДж/моль
S(кр) + O2(г) = SO2(г)  H20 = – 297 кДж/моль
H20 = – 297 кДж/моль
SO2(г) + + ½O2(г) = SO3(г)  H30 = – 101 кДж/моль
H30 = – 101 кДж/моль
H2O(ж) + SO3(г) = H2SO4(ж)  H40 = – 130 кДж/моль
H40 = – 130 кДж/моль
___________________________________________________________
H2(г) + S(кр) + 2O2(Г) = H2SO4(ж)
 рH0 =
рH0 =  H10 +
H10 +  H20 +
H20 +  H30 +
H30 +  H40 = – (286 + 297 + 101 + 130) = – 814 кДж/моль
H40 = – (286 + 297 + 101 + 130) = – 814 кДж/моль
Из приведенных расчетов видно, что независимо от того, в одну или в четыре стадии осуществлено превращение, суммарный тепловой эффект – один и тот же.
Следствия из закона Гесса
Первое следствие: тепловой эффект химической реакции равен разности между суммой энтальпий образования продуктов реакции и суммой энтальпий образования исходных веществ (с учетом стехиометрических коэффициентов в виде соответствующих множителей):
 рH0298 = рH0298 = 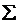 νi νi 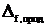 H0298 – H0298 – 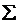 νJ νJ 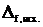 H0298 H0298 | (4.1.4) |
Второе следствие(его обычно его применяют для реакций органических соединений): тепловой эффект реакции равен разности между суммой энтальпий сгорания исходных веществ и суммой энтальпий сгорания продуктов реакции (с учетом стехиометрических коэффициентов в виде соответствующих множителей).
Применяя следствия из законов Гесса и имея справочные данные по теплотам (энтальпиям) образования (или сгорания) веществ, можно рассчитать тепловой эффект (изменение энтальпии) химических реакций.
Примеры
1) Рассчитать тепловой эффект реакции CS2(г) + 3O2(г) = CO2(г) + 2SO2(г)
Решение: в соответствии с первым следствием из закона Гесса:
 рH0 = (
рH0 = (  fH0298 CO2 + 2
fH0298 CO2 + 2  fH0298 SO2) – (
fH0298 SO2) – (  fH0298 CS2 +
fH0298 CS2 +  fH0298 O2) =
fH0298 O2) =
= [– 394 + 2×(–297)] – (117 + 3×0) = – 1105 кДж/моль
Из полученного результата видно, что эта реакция экзотермическая, и при окислении 1 моль сероуглерода в виде тепловой энергии выделяется 1105 кДж.
Следует отметить, что следствия из закона Гесса можно применять не только для химических превращений, но и для процессов, не сопровождающихся химическим превращением вещества, например, для расчета теплового эффекта изменения агрегатного состояния вещества, изменения аллотропных форм и др.
2) Рассчитать количество тепла, необходимое для испарения 1 м3 воды.
Решение: H2O(ж) = H2O(г)
 исп.H0(ж) =
исп.H0(ж) =  f H0 H20(г) –
f H0 H20(г) –  f H0 H20(ж) = –242 – (–286) = 44 кДж/моль.
f H0 H20(ж) = –242 – (–286) = 44 кДж/моль.
Для испарения 1 м3 (5,56·104 моль) воды потребуется: 44·5,56·104 =2,42·106 кДж.
Интересным может быть применение следствий из закона Гесса для сравнения химических свойств различных соединений. Например, попытка сравнить кислотные свойства амфотерных оксидов ZnO и Al2O3, исходя из положения металлов в таблице элементов, окажется малопродуктивной (разные периоды, группы, степени окисления). Попробуем сделать это сравнение, применив следствие из закона Гесса. Для этого рассчитаем изменение энтальпии в реакциях:
ZnO + Na2O = Na2ZnO2  рH0 = – 23 кДж/моль
рH0 = – 23 кДж/моль
1/2Al2O3 + 1/2Na2O = NaAlO2  рH0 = – 105 кДж/моль
рH0 = – 105 кДж/моль
При сравнении  рH0 видно, что в расчете на равное количество металла тепловой (экзо-) эффект реакции с участием оксида алюминия больше, следовательно, кислотные свойства Al2O3 выражены сильнее, чем у ZnO.
рH0 видно, что в расчете на равное количество металла тепловой (экзо-) эффект реакции с участием оксида алюминия больше, следовательно, кислотные свойства Al2O3 выражены сильнее, чем у ZnO.
Многочисленные термохимические исследования, накопленный фактический материал были предпосылкой считать тепловой эффект химической реакции критерием возможности или невозможности ее самопроизвольного протекания, преимущественного направления превращения веществ при нескольких вариантах (см. принцип Бертло–Томсена).
Однако были известны и другие факты. Например, при нормальных условиях испаряются не только жидкости (вода, эфир и т.д.), но даже твердые тела (пример – возгонка кристаллического иода), хотя известно, что испарение – это эндотермический процесс. Другим примером могут быть процессы растворения некоторых веществ. Так, растворение селитры в воде – настолько эндотермичный процесс, что посуда запотевает за счет конденсации атмосферной влаги. Причем растворимость (моль/л) селитры больше растворимости кальцинированной соды, хотя в последнем случае тепло не поглощается, а выделяется.
Перечисленные примеры вызывают естественные вопросы.
1) Всегда ли реакция, для которой  рH0 более отрицательна, энергетически более выгодна?
рH0 более отрицательна, энергетически более выгодна?
2) Как с позиций термохимии объяснить химическое равновесие? Если протекание экзотермической реакции понятно, то почему самопроизвольно протекает обратная эндотермическая реакция?
3) Можно ли по знаку  рH0 < 0 или
рH0 < 0 или  рH0 > 0 надежно определить преимущественное направление реакции?
рH0 > 0 надежно определить преимущественное направление реакции?
Из приведенных выше примеров следует, что изменение энтальпии – это не единственный критерий преимущественного направления и степени протекания реакции. Что же является дополнительной движущей силой самопроизвольного протекания эндотермических реакций?
Для ответа на этот вопрос обсудим, что меняется в системах, например при испарении или растворении веществ (кристаллов)? Общее в этих превращениях то, что системы переходят из более упорядоченного состояния в более хаотичные, неупорядоченные состояния. Поскольку с позиций термохимии эти превращения часто невыгодны, то конкурирующей энергетической составляющей самопроизвольно протекающего процесса является, по-видимому, стремление к увеличению беспорядка.
Мерой неупорядоченности системы в химической термодинамике является энтропия (S).
4.2 Понятие об энтропии. Энергия Гиббса и направление химической реакции
Строгое определение энтропии будет дано в курсе физической химии. Для решения задач в рамках данного курса определим наиболее существенное. Во-первых, S = 0 только для идеального кристалла при Т = 0 (этот постулат называют третьим началом термодинамики). Для реальных систем и условий энтропия всегда положительна. Чем сложнее по составу система и чем менее она упорядочена, тем больше ее энтропия.
Например, если вещество может существовать в нескольких агрегатных состояниях, то Sтв< Sж<< Sг. Если сравнить энтропию нескольких газообразных веществ: He и Ar, N2 и O2, CO2 и SO2, то SHe < SAr, т.к. атом аргона более сложен по составу (прежде всего из-за большего числа электронов); SN2 < SO2 вследствие того, что в молекуле азота более прочная тройная связь; SCO2 < SSO2 вследствие того, что атом серы сложнее по составу, чем атом углерода, а также из-за различия в строении молекул: молекула CO2 имеет линейную структуру, а SO2 – угловую. По этой причине в молекуле SO2 кроме колебаний атомов кислорода вдоль связи с серой возможны колебания с изменением валентного угла.
Изменение энтропии в химической реакции подчиняется закону Гесса, и рассчитать ее, как и изменение энтальпии, можно, используя следствия из этого закона:
 рS0298 = рS0298 = 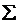 νiS0298 - νiS0298 - 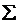 νJS0298 νJS0298 | (4.2.1) |
Стандартные энтропии веществ, в т.ч. и простых, приводятся в справочниках (S0, Дж/моль.К).
Согласно законам термодинамики, в изолированной системе самопроизвольно могут протекать только такие реакции, которые ведут к увеличению неупорядоченности системы, т.е. к увеличению энтропии (второе начало термодинамики).
Если проанализировать зависимость направления реакции от изменения энтальпии и энтропии, то нетрудно заметить, что эти факторы оказываются конкурирующими. Действительно, выделение теплоты в реакции будет тем большим (и тем выгоднее такая реакция), чем более прочные связи, по сравнению с исходными, образуются. Однако при образовании более прочных связей система переходит в состояние с меньшей энтропией, что энергетически невыгодно.
Действие обоих факторов, энтальпийного и энтропийного, учитывает энергетическая характеристика, введенная в физхимию Гиббсом, и носящее его имя – энергия Гиббса (G):
| G = H – TS | (4.2.2) |
Термодинамика утверждает, что в любой закрытой системе при постоянном давлении и температуре возможен только такой самопроизвольный процесс, при котором энергия Гиббса уменьшается, т.е. процесс, для которого  рG < 0.
рG < 0.
Для химических реакций, проводимых при постоянном давлении (Р = 101 кПа) и температуре (Т), изменение энергии Гиббса (стандартное изменение энергии Гиббса) рассчитывают по формуле:
 рGТ0 = рGТ0 =  рHТ0 – T рHТ0 – T  рSТ0 рSТ0 | (4.2.3) |
Рассмотрим варианты, возможные при проведении химических процессов: а)  рHТ0 < 0,
рHТ0 < 0,  рSТ0 > 0; в этих случаях
рSТ0 > 0; в этих случаях  рGТ0 < 0 при любых Т, и такой процесс термодинамически возможен при любой температуре;
рGТ0 < 0 при любых Т, и такой процесс термодинамически возможен при любой температуре;
б)  рHТ0 < 0,
рHТ0 < 0,  рSТ0 < 0; в этих случаях
рSТ0 < 0; в этих случаях  рGТ0 < 0, если Т <
рGТ0 < 0, если Т <  рHТ0/
рHТ0/  рSТ0, т.е. реакция возможна при относительно низких температурах;
рSТ0, т.е. реакция возможна при относительно низких температурах;
в)  рHТ0 > 0,
рHТ0 > 0,  рSТ0 > 0; в этих случаях
рSТ0 > 0; в этих случаях  рGТ0 < 0, если Т >
рGТ0 < 0, если Т >  рHТ0/
рHТ0/  рSТ0, т.е. реакция возможна при относительно высоких температурах;
рSТ0, т.е. реакция возможна при относительно высоких температурах;
г)  рHТ0 > 0,
рHТ0 > 0,  рSТ0 < 0; в этих случаях
рSТ0 < 0; в этих случаях  рGТ0 > 0 при любой Т, и процесс термодинамически невыгоден при любой температуре.
рGТ0 > 0 при любой Т, и процесс термодинамически невыгоден при любой температуре.
Если  рSТ0 » 0 (например, если в реакции участвуют и образуются твердые вещества), то величина и знак
рSТ0 » 0 (например, если в реакции участвуют и образуются твердые вещества), то величина и знак  рGТ0 определяются изменением энтальпии
рGТ0 определяются изменением энтальпии  рHТ0; именно такие реакции подчиняются принципу Бертло–Томсена (см. ранее).
рHТ0; именно такие реакции подчиняются принципу Бертло–Томсена (см. ранее).
При  рGТ0 = 0, т.е.
рGТ0 = 0, т.е.  рHТ0 = Т
рHТ0 = Т  рSТ0 в системе устанавливается подвижное термодинамическое равновесие, при котором прямая и обратная реакция равновероятны. Температуру, соответствующую состоянию равновесия, можно рассчитать: Т =
рSТ0 в системе устанавливается подвижное термодинамическое равновесие, при котором прямая и обратная реакция равновероятны. Температуру, соответствующую состоянию равновесия, можно рассчитать: Т =  рHТ0/
рHТ0/  рSТ0.
рSТ0.
Изменение энергии Гиббса химической реакции в стандартных условиях можно рассчитать, либо используя уравнение (4.2.3), либо по стандартным энергиям Гиббса (  fG0298), применяя следствие из закона Гесса:
fG0298), применяя следствие из закона Гесса:
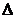 рG0 = рG0 =  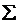 νi νi  fG0 - fG0 - 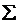 νJ νJ  fG0 fG0 | (4.2.4) |
Стандартные энергии Гиббса образования веществ приводятся в справочниках. Для простых веществ, находящихся в термодинамически устойчивых состояниях,  Gf0298 = 0 (также как и
Gf0298 = 0 (также как и  Hf0298).
Hf0298).
Используя для расчетов уравнение (4.2.3), следует согласовать размерности  Hf0298 и S0298, кДж/моль и Дж/моль·К.
Hf0298 и S0298, кДж/моль и Дж/моль·К.
В качестве примера рассмотрим возможность реализации следующего превращения: CO2(г) « Cалмаз + O2(г).
Для решения такой задачи не потребуются даже справочные данные. Известно, что обратная реакция – окисление углерода (в любой форме) кислородом – экзотермическая реакция. Следовательно, прямая реакция – эндотермическая, поэтому для нее  рH0> 0. Знак
рH0> 0. Знак  рS0 определить тоже несложно: энтропией твердого углерода можно пренебречь по сравнению с энтропией газообразных веществ, а энтропия более сложной молекулы CO2 больше, чем O2. Следовательно,
рS0 определить тоже несложно: энтропией твердого углерода можно пренебречь по сравнению с энтропией газообразных веществ, а энтропия более сложной молекулы CO2 больше, чем O2. Следовательно,  рS0 < 0, и
рS0 < 0, и  рGТ0 > 0. Таким образом, прямая реакция самопроизвольно не пойдет при любой температуре.
рGТ0 > 0. Таким образом, прямая реакция самопроизвольно не пойдет при любой температуре.
Химическое равновесие
В состоянии химического равновесия прямая и обратные реакции термодинамически равновероятны (  рG0 = 0). При этом параметры системы (температура, давление, концентрации) остаются неизменными во времени, т.к. скорости прямой и обратной реакций равны.
рG0 = 0). При этом параметры системы (температура, давление, концентрации) остаются неизменными во времени, т.к. скорости прямой и обратной реакций равны.
Следует различать истинное и «заторможенное» (ложное) равновесие.
Если равновесие «заторможенное», то параметры системы (давление, температура, концентрации) при некоторых условиях не меняются во времени, хотя равновесия при этом может и не быть. Например, смесь газообразного водорода с хлором (или с кислородом) при обычных условиях может существовать без каких-либо изменений весьма продолжительное время. Однако стоит только ввести в смесь подходящий катализатор (платиновую чернь, например), смесь взорвется и в исходное состояние самопроизвольно не вернется.
Признаки истинного равновесия:
– термодинамическая устойчивость, т.е. в отсутствие внешних воздействий оно характеризуется постоянством равновесного состава системы;
– подвижность, т.е. при изменении условий соотношение компонентов в системе меняется (за счет преимущественного протекания одной из реакций), но при восстановлении первоначальных условий восстанавливается исходное соотношение веществ (вследствие преимущественного протекания обратной реакции, до наступления равновесия);
В состоянии равновесия понятия «исходные вещества» и «продукты реакции» в общем-то, неразличимы, т.к. одновременно все вещества, образующие систему, оказываются реагентами (протекают и прямая, и обратная реакции). В то же время, для удобства, вещества левой части уравнения реакции обычно называют «исходными», а те, что справа, за знаком равновесия («), – «продуктами». В качестве истинно равновесной системы можно рассматривать, например, смесь CO2, H2, CO и H2O, полученную в результате реакции
CO2(г) + H2(г) « CO(г) + H2O(г).
При Т = 8100С (над катализатором) эта смесь будет существовать в эквимолярном соотношении сколь угодно долго. Если температуру смеси увеличить, то будет протекать преимущественно прямая реакция, но если восстановить Т = 8100С, соотношение реагентов вновь станет первоначальным.
– возможность достижения равновесного состояния различными способами.
Например, рассмотренную выше равновесную смесь CO2, H2, CO и H2O можно получить в результате реакции:
а) CO2 и H2; б) CO2, H2, CO; в) CO и H2O
При этом независимо от исходных мольных соотношений реагентов при достижении равновесия соотношение CO2, H2, CO и H2O будет одинаковым, соответствующим закону действующих масс.
Закон действующих масс: в состоянии химического равновесия отношение произведения равновесных молярных концентраций продуктов реакции к произведению равновесных молярных концентраций исходных веществ (в степенях, соответствующих стехиометрическим коэффициентам) есть величина постоянная при постоянстве температуры и называется константой химического равновесия (К).
Например, для условной гомогенной равновесной системы
aA + bB « dD + qQ закон действующих масс выражается следующим уравнением:
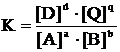 | (4.3.1) |
В уравнении (4.3.1) [A], [B], [D], [Q], – равновесные концентрации (моль/л) всех веществ – участников реакции, т.е. концентрации, которые устанавливаются в системе в момент химического равновесия; степеней a, b, d, q – стехиометрические коэффициенты в уравнении реакции.
Константа равновесия зависит только от природы реагирующих веществ и температурыи не зависит от того, из какого исходного состояния равновесие достигнуто.
Как отмечалось ранее, термодинамическим условием химического равновесия является равенство нулю изменения энергии Гиббса:  рGТ = 0.
рGТ = 0.
Связь константы равновесия с энергией Гиббса описывается уравнениями:
 рGТ0 = – RTlnK K = exp(– рGТ0 = – RTlnK K = exp(–  рGТ0/RT) рGТ0/RT) | (4.3.2) |
Из уравнения (4.3.2) следует, что чем отрицательнее величина  рGТ0, тем больше величина константы равновесия, и (см. уравнение 4.3.1) тем большей будет концентрация продуктов по сравнению с исходными веществами.
рGТ0, тем больше величина константы равновесия, и (см. уравнение 4.3.1) тем большей будет концентрация продуктов по сравнению с исходными веществами.
Например, рассчитаем константу для равновесия N2+3H2 « 2NH3 при Т = 500 К:  Gf0298 = – 16,5 кДж/моль, и при Т = 500 К
Gf0298 = – 16,5 кДж/моль, и при Т = 500 К
K = exp(16500)/8,31 · 500) = 3,97
Если K >> 1, то прямое превращение протекает в большей мере, чем обратное.
Если K << 1, то в прямом направлении реакция протекает незначительно; в большей мере протекает обратная реакция.
Если К 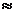 1, то равновероятны как прямое, так и обратное превращение веществ.
1, то равновероятны как прямое, так и обратное превращение веществ.
Очевидно, что при выборе варианта получения (превращения) заданного вещества предпочтительнее тот, для которого константа больше.
Примеры применения закона действующих масс (з.д.м.)
1) Константа равновесия для гомогенной равновесной системы
а) N2+3H2 « 2NH3 имеет следующий вид:
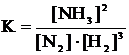
б) Константа равновесия диссоциации слабого электролита, например фтороводородной кислоты: HF « H+ + F– имеет вид:
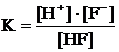 – такие константы называют константами диссоциации (Кдис.) и они приводятся в справочниках. Чем слабее электролит, тем меньше Кдис.
– такие константы называют константами диссоциации (Кдис.) и они приводятся в справочниках. Чем слабее электролит, тем меньше Кдис.
2) Если в гомогенной равновесной системе какой-либо реагент в большом избытке по сравнению с остальными, то его не включают в выражение константы.
Пример: равновесие гидролиза F– + H2O « HF + OH–, в котором H2O не только реагент, но и растворитель, следовательно, в большом избытке. С учетом последнего запишем выражение константы гидролиза:
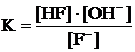
3) Если система гетерогенная, то реакция протекает на границе раздела фаз, и поэтому реагент более упорядоченной фазы в выражение константы не включают.
Пример: в насыщенном растворе фосфата кальция устанавливается гетерогенное равновесие между осадком и раствором:
Ca3(PO4)2(тв.) « 3Ca2+(р-р)+2PO43–(р-р)
при этом два реагента (Ca2+ и PO43–) находятся в жидкой фазе (растворе), а третий, Ca3(PO4)2, – в осадке; последний не включается в выражение константы равновесия: K = [Ca2+]3[PO43–]2
Для насыщенных растворов малорастворимых солей такие константы называют произведением растворимости (ПР) и они приводятся в справочниках.
4) Если в равновесии участвуют газообразные вещества, то в выражении константы их молярные концентрации можно заменить парциальными давлениями (px).
Пример: дляравновесия 2SO2 + O2 « 2SO3 выражение константы можно записать в двух вариантах:
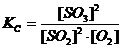 Кр =
Кр = 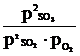
Смещение химического равновесия. Принцип Ле Шателье
Если не меняются условия, при которых установилось химическое равновесие, то соотношение реагентов в системе не меняется во времени. При внешнем воздействии (нагревании или охлаждении системы, повышении или понижении давления, добавлении или удалении какого-либо реагента, участвующего в реакции) равновесие нарушается (смещается). Нарушение равновесия проявляется в том, что одна из реакций (прямая или обратная) начинает идти с большей скоростью.
Если в результате воздействия увеличивается скорость прямой реакции, то говорят, что равновесие смещается вправо. Если увеличивается скорость обратной реакции – смещается влево.
Через некоторое время, по мере расхода одних реагентов и увеличения концентрации других, скорости прямой и обратной реакций сравняются, и установится новое равновесие. Если в первоначальном и в конечном состояниях температура одинакова, то константа нового равновесия будет прежней, но соотношение реагентов будет другим.
Принцип Ле Шателье: если на систему, находящуюся в состоянии химического равновесия, оказывается какое-либо внешнее воздействие, то равновесие в результате протекающих в системе процессов сместится таким образом, что оказанное воздействие уменьшится.
Влияние изменения концентраций на равновесие
При увеличении концентрации какого-либо из веществ, участвующих в реакции, равновесие смещается в сторону расходования этого вещества, а при её уменьшении – в сторону образования этого вещества.
Пример 1. Если в смесь SO2, O2, SO3, находящуюся в равновесии,
2SO2 + O2 « 2SO3, добавить O2, то в соответствии с принципом Ле Шателье добавленный кислород будет расходоваться, т.е. преимущественно будет протекать прямая реакция окисления SO2, равновесие сместится вправо, выход SO3 увеличится.
К аналогичному выводу можно прийти, анализируя закон действующих масс (з.д.м.) для этого равновесия: 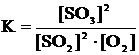
При добавлении O2 знаменатель дроби увеличится, равновесие нарушится, и для того, чтобы соотношение реагентов соответствовало з.д.м. (т.е. константа осталась прежней), концентрации SO2 и O2 должны уменьшаться, а концентрация SO3 – увеличиваться, а для этого должна преимущественно протекать прямая реакция.
Через некоторое время установится новое состояние равновесия. Как изменятся концентрации реагентов в сравнении с исходными? Очевидно, что концентрация SO2 уменьшится, а концентрация SO3 увеличится. А как изменится концентрация O2? Она будет меньшей, чем в момент его добавления, но большей, чем в исходном равновесии, т.к. добавка расходуется не полностью.
Пример 2. Изменением концентраций каких реагентов можно сместить влево равновесие? Ca3(PO4)2(тв.) « 3Ca2+(р-р)+2PO43–(р-р)
Решение: в соответствии с принципом Ле Шателье сместить равновесие влево можно либо уменьшая концентрацию исходных веществ, либо увеличивая концентрации продуктов.
В данном примере к изменению концентрации твердого Ca3(PO4)2 равновесие не чувствительно (см. ранее особенности з.д.м. для гетерогенных равновесий). Следовательно, сместить равновесие влево можно, увеличив концентрацию либо Ca2+, либо PO43–. Первый вариант можно осуществить, добавив в раствор хорошо растворимую соль кальция, например, Ca(NO3)2. Увеличить концентрацию PO43– можно добавлением хорошо растворимого Na3PO4.
Одинаковым ли будет эффект смещения равновесия, если в одном случае увеличить вдвое концентрацию Ca2+, а в другом, также вдвое, увеличить концентрацию PO43–? Ответ на этот вопрос можно получить из выражения константы равновесия K = [Ca2+]3·[PO43–]2 .
Из этого уравнения видно, что поскольку показатели степеней при концентрациях реагентов разные, то и эффект от изменения концентраций будет разным.
Химическое равновесие более чувствительно к изменению концентрации того реагента, для которого в выражении константы показатель степени при концентрации больше (т.е. больший коэффициент в уравнении реакции).
Таким образом, при увеличении в равное число раз концентраций Ca2+ или PO43– эффект от изменения концентрации Ca2+ будет большим.
Пример 3. Как влияет разбавление раствора на равновесие диссоциации
HF « H+ + F–
Напишем выражение з.д.м. для этого равновесия: 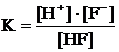
На первый взгляд добавление H2O не должно изменить равновесия, т.к. в уравнении реакции вода не фигурирует и в выражение константы она не входит. Однако разбавление раствора проявляется в другом: в изменении (уменьшении) концентраций реагентов, участвующих в равновесии и включенных в з.д.м. Действительно, если раствор разбавить вдвое, то (см. выражение К) знаменатель дроби уменьшится в два раза, а числитель – в четыре (22).
Для того чтобы соотношение реагентов соответствовало з.д.м. (т.е. константа осталась прежней), необходимо, чтобы знаменатель дроби уменьшился, а числитель – увеличился. Очевидно, что это реализуется в случае, если продиссоциирует дополнительное количество HF. Следовательно, при разбавлении данного раствора равновесие смещается вправо (степень диссоциации кислоты увеличится).
