Квантовомеханическая модель строения атома

Гейзенберг указал на принципиальные различия в наблюдении за микро- и макрообъектами. Наблюдение за любым объектом, в принципе, сводится к двум случаям:

1) Объект сам подает какие-либо сигналы. Например, шум от работающего двигателя, тепловое излучение и т. п.

2) На наблюдаемый объект оказывается какое-то воздействие, например, облучение светом, радиоволнами и т. п., и регистрируется отраженный сигнал (как это широко используется в радиолокации, в эхолокации). Причем, чем сильнее воздействие на наблюдаемый объект, тем сильнее (при прочих равных условиях) отраженный сигнал и надежнее регистрация объекта.

Если ведется наблюдение за привычными для нас макрообъектами, то действие на них электромагнитного излучения (свет, радиоволны и т. д.) не изменяют ни их положения, ни их скорости. Совершенно иначе обстоит дело при наблюдении объектов микромира, например, электронов. При действии кванта света на электрон скорость последнего не остается без изменения. Поэтому, определив при действии фотона положение электрона в какой-то момент времени, мы не в состоянии в это же мгновение определить его скорость – она уже изменилась.

Гейзенберг предложил соотношение, которое получило название «соотношение неопределенностей»:

DpDx > 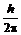, (14)

где Dp – неопределенность в значении импульса частицы, а Dx – не-определенность в ее координатах. Из этого соотношения следует, что чем точнее определены координаты электрона, тем с меньшей точностью будет определен его импульс и наоборот. Иными словами, говорить о траектории электрона не имеет смысла, так как для описания последней необходимо точно знать и координаты электрона и его импульс в каждый момент времени (что было заложено в модель атома Бора). Соотношение неопределенностей показывает, что столь точное описание движения такой маленькой частицы, как электрон, невозможно, т. е. само понятие орбита (траектория) электрона оказывается несостоятельным. Необходим совершенно иной метод описания поведения электрона в атоме, который дает квантовая механика. В квантовой механике для описания поведения электрона исходными являются два положения:

1) движение электрона носит волновой характер;

2) наши знания о поведении электрона имеют вероятностный (или статистический) характер.

Некоторые разъяснения по первому положению были уже даны (на стр. 25). Прокомментируем второе положение. В соответствии с принципом неопределенности Гейзенберга никогда нельзя точно установить место нахождения частицы. Лучшее, что можно сделать в этом случае, это указать вероятность, с которой частица будет находиться в области пространства DV = Dx × Dy × Dz.

В 1926 г. Шредингер предложил уравнение, в которое для описания поведения электрона в атоме была введена волновая функция. Уравнение имеет обманчиво простой вид:

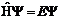, (15)

где E – полная энергия частицы, Y – волновая функция, 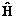– оператор Гамильтона. Гамильтониан показывает, какие математические операции нужно произвести с волновой функцией, чтобы решить уравнение относительно энергии. Физический смысл волновой функции определить трудно, а вот квадрат модуля ее | Y |² определяет вероятность нахождения электрона в данной области пространства.

Уравнение Шредингера точно решается для водорода и водородоподобных атомов (т. е. для систем, состоящих из ядра и одного электрона). Из решения этого уравнения для атома водорода вытекало, что поведение электрона в атоме описывается четырьмя квантовыми числами.

1°. Главное квантовое число n. Оно может принимать значения от 1 до бесконечности, которые определяют:

а) номер энергетического уровня (в теории Бора – номер орбиты);

б) интервал энергий электронов, находящихся на этом уровне;

в) размеры орбиталей (в теории Бора – радиусы орбит);

г) число подуровней данного энергетического уровня (первый уровень состоит из одного подуровня, второй – из двух, третий – из трех и т. д.).

д) в Периодической системе Д. И. Менделеева значению главного квантового числа соответствует номер периода.

Иногда пользуются буквенными обозначениями главного квантового числа, т. е. каждому численному значению n соответствует определенное буквенное обозначение:

Таблица 7
Буквенные обозначения главного квантового числа

Численные значенияn
Буквенное обозначение	K	L	M	N	O

2°. Орбитальное или азимутальное квантовое число l. Орбитальное квантовое число определяет момент количества движения (момент импульса) электрона, точное значение его энергии и форму орбиталей.

Новое понятие «орбиталь» по звучанию напоминает слово «орбита», но имеет совершенно иной смысл. Орбиталь – это область пространства, в которой вероятность нахождения электрона имеет определенное значение (90 – 95 %). Иногда орбиталью называют граничную поверхность этой области, а на рисунках, как правило, изображают сечение этой области плоскостью, проходящей через начало координат и лежащей в плоскости рисунка. В начало координат помещают центр ядра атома. Понятие орбиталь, в отличие от орбиты, не подразумевает знания точных координат электрона. Орбитальное квантовое число зависит от главного квантового числа и принимает следующие значения:

l = 0, 1, … , (n – 1),

причем каждому значению главного квантового числа n соответствует n значений орбитального квантового числа l. Например, если n = 1, то l принимает только одно значение (l = 0) при n = 2 величина l принимает двазначения: 0 и 1 и т. д. Каждому численному значению l соответствует определенная геометрическая форма орбиталей и приписывается буквенное обозначение. Первые четыре буквенныx обозначения имеют историческое происхождение и связаны с характером спектральных линий, соответствующих электронным переходам между этими подуровнями: s, p, d, f – первые буквы английских слов, использованных для названия спектральных линий sharp (резкий), principal (главный), diffuse (диффузный), fundamental (основной). Обозначения других подуровней идут в алфавитном порядке: g, h, … .

Таблица 8
Число подуровней, определяемых значением n

Значениеn

Значение l

Буквенное обознач. l

s

s

p

s

p

d

s

p

d

f

s

p

d

f

g

Число подуровней

Любой подуровень определяется двумя квантовыми числами – главным (при записи обычно указывают численное значение) и орбитальным (при записи обычно используют буквенное обозначение ). Например, энергетический подуровень, для которого n = 2 и l = 1 следует записать так: 2p-подуровень. Все орбитали с одинаковыми значениями l имеют одинаковую геометрическую форму и, в зависимости от значений главного квантового числа различаются размерами, т. е. являются подобными фигурами. Например, все орбитали, для которых l = 0 (s-орбитали) имеют форму сферы, но различаются радиусами, в зависимости от значения главного квантового числа n. Чем больше значение n, тем больше размеры орбиталей, например, 1s-орбиталь имеет наименьшие размеры, радиус 2s-орбитали больше, 3s-еще больше.

3°. Магнитное квантовое число m_l . Вращение электрона вокруг ядра можно сравнить с движением тока по замкнутому контуру. При этом возникает магнитное поле, напряженность которого направлена перпендикулярно плоскости вращения электрона. Если атом находится во внешнем магнитном поле, то, согласно квантовомеханическим представлениям, его электроны должны расположиться так, чтобы проекции их магнитных моментов на направление этого поля были целочисленными (см. рис. 3). При этом они могут принимать как отрицательные, так и положительные значения, включая нулевое.

Численное значение проекции магнитного момента и является магнитным квантовым числом. Если значение орбитального квантового числа равно l, то магнитное квантовое число будет принимать значения от – l до + l, включая ноль. Общее количество значений будет равно 2l + 1.

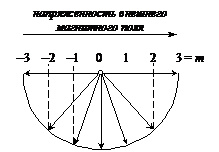
Рис. 3. Физический смысл магнитного квантового числа

Таким образом, магнитное квантовое число определяет расположение орбиталей в пространстве относительно выбранной системы координат. Общее число возможных значений m_l показывает, сколькими способами можно расположить орбитали данного подуровня в пространстве, т. е. общее число орбиталей на подуровне.

Таблица 9
Число орбиталей на подуровне

n				...
l							...
ml			– 1, 0, + 1		– 1, 0, + 1	– 2, – 1, 0, + 1, + 2	...
Число орбиталей на подуровне							...

Орбитальному квантовому числу l = 0 соответствует единственное значение магнитного квантового числа m_l = 0. Эти значения характеризуют все s-орбитали, которые имеют форму сферы. Т. к. в этом случае магнитное квантовое число принимает только одно значение, каждый s-подуровень состоит только из одной орбитали. Рассмотрим любой p-подуровень: при l = 1 орбитали имеют форму гантелей (объемные «восьмерки»), магнитное квантовое число принимает следующие значения m_l = – 1, 0, + 1 (три значения), следовательно, p-подуровень состоит из трех орбиталей, и эти орбитали располагаются вдоль трех осей координат и, соответственно, обозначаются p_x, p_y, p_z. Для d-подуровня l = 2, m_l = – 2, – 1, 0, + 1, + 2 (5 значений), и любой d-подуровень состоит из пяти орбиталей, которые определенным образом расположены в пространстве (см. рис. 6) и соответственно обозначаются d_xy, d_xz, d_zy, 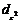и . 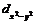Четыре из пяти d-орбиталей имеют форму четырехлепестковых розеток, каждая из которых образована двумя гантелями, пятая орбиталь представляет собой гантель с тором в экваториальной плоскости ( 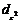-орбиталь) и расположена вдоль оси z. «Лепестки» орбитали 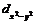расположены вдоль осей x и y. Орбитали d_xy, d_xz и d_yz расположены между соответствующими осями.

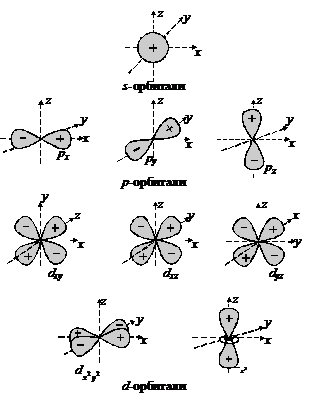
Рис. 4. Пространственные конфигурации s-, p- и d-орбиталей

Четвертый энергетический уровень состоит из четырех подуровней – s, p, d и f. Первые три из них аналогичны рассмотренным выше, а четвертый – f-подуровень состоит уже из семи орбиталей, пространственные конфигурации которых достаточно сложны, и рассматривать их мы не будем.

4°. Спиновое квантовое число (спин электрона), m_s. В 1926 г. Уленбек и Голдсмит показали, что помимо орбитального движения электрон должен участвовать во вращении вокруг собственной оси, проходящей через центр. Поэтому электрон должен иметь собственный момент импульса, а так как он является заряженной частицей, то и магнитный момент. Это представление довольно примитивно, но используется для наглядности, поэтому мы будем им пользоваться. Возможны только два направления вращения электрона вокруг своей оси: по и против часовой стрелки. Следовательно, спиновое квантовое число принимает лишь два значения: 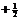и .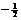

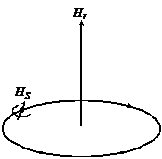
Рис. 5. Возникновение спина электрона (согласно Уленбеку и Голдсмиту)

Таким образом, состояние электрона в атоме определяется набором значений четырех квантовых чисел. Понятие «орбиталь» было дано выше (см. стр. 29). Определим четче некоторые термины, которые использовались при разъяснении физического смысла квантовых чисел и будут использоваться в дальнейшем.

Группа орбиталей, имеющих одинаковое значение орбитального квантового числа, образует энергетический подуровень.

Совокупность всех орбиталей с одинаковым значением главного квантового числа, т. е. орбиталей с близкими значениями энергий, образует энергетический уровень.

Если при описании строения атома водорода не возникает особых проблем – всего один электрон, который в основном состоянии должен занимать орбиталь с минимальной энергией, то при описании строения многоэлектронных атомов необходимо учитывать взаимодействие электрона не только с ядром, но и с другими электронами. Отсюда возникает проблема последовательности заполнения электронами различных подуровней в атоме. Эта последовательность определяется тремя «правилами».

1. Принцип Паули. В одном атоме не может быть двух электронов с одинаковым набором значений всех четырех квантовых чисел.

Это означает, что электроны должны отличаться значением хотя бы одного квантового числа. Первые три квантовых числа характеризуют орбиталь, на которой находится электрон. И если два электрона имеют одинаковый их набор, то это означает, что они находятся на одной и той же орбитали. В соответствии с принципом Паули они должны отличаться значением спина. Из этого следует, что на одной орбитали могут находится только два электрона с противоположными по знаку значениями спина.

Для определения «емкости» энергетического уровня, т. е. максимального числа электронов, которые могут находиться на уровне с главным квантовым числом n, составим следующую таблицу:

Таблица 10
Максимальная электронная емкость первых трех энергетических уровней

n	l	ml	s	число электронов на подуровне
	0(s)		±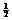
	0(s)		±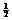
	1(p)	–1, 0, +1	±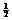
	0(s)		±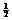
	1(p)	–1, 0, +1	±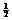
	2(d)	–2, –1, 0, +1, +2	±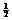

Из таблицы видно, что число орбиталей на данном энергетическом уровне в зависимости от значения n образует арифметическую прогрессию, где первый член a₁ = 1, а последний – a_n = 2l + 1. Разность прогрессии равна 2, а число членов – n. Сумма S_n прогрессии в этом случае будет равна:

S_n = 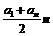= = 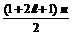(l + 1)n,

а с учетом l = n – 1

S_n = (n – 1 + 1)n = n².

Таким образом, общее число орбиталей на энергетическом уровне со значением главного квантового числа n равно n². А так как на одной орбитали может находиться лишь два электрона, получаем, что максимальная электронная емкость энергетического уровня составляет 2n².

Существует определенная форма записи состояния электрона в атоме. Например, для основного состояния атома водорода она выглядит так:

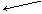		число электронов
Уровень	1s1
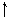	подуровень

Это означает, что на первом энергетическом уровне на s-подуровне находится один электрон. Существует и другая форма записи распределения электронов по подуровням – с помощью квантовых ячеек. Орбиталь в этом случае принято условно обозначать квадратами, а электроны – стрелками ­ или ¯, в зависимости от знака спина. Тогда электронное строение атома водорода можно изобразить так:

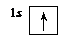
Электронное строение атома с бóльшим числом электронов, например атома бора, можно записать следующими способами:

1s²2s²2p¹ или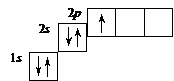

2. Правило Хунда. Это правило определяет последовательность заполнения орбиталей электронами в пределах одного подуровня.

Правило Хунда формулируется так: «В пределах одного подуровня электроны располагаются по орбиталям таким образом, чтобы их суммарный спин был максимальным, т. е. на подуровне должно быть максимальное число неспаренных электронов». Рассмотрим выполнение этого правила на примере заполнения p-подуровня.

1 вариант суммарный спин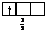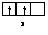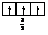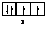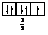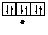
2 вариант суммарный спин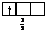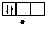

В соответствии с правилом Хунда заполнение орбиталей происходит по первому варианту, т. е. сначала электроны занимают все свободные орбитали и только потом происходит их спаривание.

3. Принцип наименьшей энергии (правило Клечковского). Заполнение энергетических уровней в водородоподобных атомах (микросистема, состоящая из ядра и одного электрона) происходит в соответствие с монотонным ростом главного квантового числа n (n = 1, 2, 3, … и т. д.). При каждом значении n заполнение подуровней должно осуществляться в порядке возрастания орбитального квантового числа l, которое принимает значения от 0 до (n – 1). И заполнение следующего энергетического уровня начинается только в том случае, когда предыдущий уровень заполнен полностью. Максимальное число электронов на энергетическом уровне определяется формулой 2n² и, следовательно, максимальные числа электронов в периодах должны быть следующими:

Таблица11
Предполагаемое число электронов в периодах

№ периода (n)	Максимальное число электронов

Реально же в Периодической системе наблюдается другая картина:

Таблица12
Реальное число электронов в периодах

№ периода (n)	Максимальное число электронов

Как видно из этой таблицы, периоды располагаются парами, исключение составляет только первый период, содержащий всего два элемента, у которых заполняется первый энергетический уровень, состоящий из одного подуровня, и нет внутренних электронов, которые могли бы повлиять на строение внешнего уровня. В остальных же случаях наблюдается следующая картина: строение третьего периода подобно строению второго (и оба содержат по 8 элементов), строение пятого периода подобно строению четвертого (и в обоих по 18 элементов), – седьмого подобно строению шестого (по 32 элемента).

Значительно лучшее совпадение с действительностью дает распределение электронов по (n + l) группам, предложенное В. М. Клечковским: «В атоме каждый электрон занимает тот подуровень, на котором его энергия будет минимальной».

Выше указывалось, что энергия электрона определяется не только значением главного квантового числа, но и значением орбитального, поэтому для того, чтобы определить, какой подуровень будет заполняться электронами в первую очередь, необходимо учитывать значения обоих квантовых чисел.

Для практического применения правило Клечковского можно сформулировать так:

а) «Заполнение подуровней электронами происходит в последовательности увеличения суммы соответствующих им значений главного и орбитального квантовых чисел».

б) «В случае одинаковых значений этой суммы для нескольких подуровней, заполняется сначала тот подуровень, для которого главное квантовое число имеет наименьшее значение».

Рассмотрим конкретное применение этого правила:

Таблица 13
Сумма значений главного и побочного квантового числа

n

l

n + l

Для первых двух значений сумм (n + l), равных соответственно 1 и 2, нет альтернативных вариантов, и заполнение подуровней происходит в следующей последовательности: 1s и затем 2s. Начиная со значения суммы, равной 3, возникают два варианта: заполнять 2p-подуровень или 3s-подуровень. В соответствии с правилом Клечковского, выбираем тот подуровень, для которого n имеет меньшее значение, т. е. 2p-подуровень. Затем заполняется 3s-подуровень. Далее значение n + l = 4. Таких значений опять два: для 3p-подуровня и для 4s-подуровня (случай, аналогичный предыдущему). Сначала будет заполняться 3p-, а затем 4s-подуровень. 3d-подуровень остается свободным, так как сумма n + l для него больше, чем для 4s.

Применяя правило Клечковского, получим следующую последовательность заполнения энергетических подуровней:

1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 4f 5d 6p.

Но такое заполнение происходит до определенного момента. Если рассмотреть изменение энергии подуров­ней с увеличением заряда ядра атома (см. рис. 8), то можно увидеть, что энергия всех подуровней снижается. Но скорость понижения энергии у разных подуровней не одинакова. Поэтому, если до кальция 3d-подуровень был по энергии выше 4s, то начиная со скандия и последующих элементов, его энергия резко снижается, о чем говорит, например, электронное строение иона Fe²⁺ (1s²2s²2p⁶3s²3p⁶3d⁶). Из приведенного электронного строения иона видно, что два валентных электрона железа ушли с менее энергетически выгодного 4s-подуровня. Аналогичная инверсия энергий наблюдается у 5s- и 4f-, а также у 6s- и 5f-подуровней.

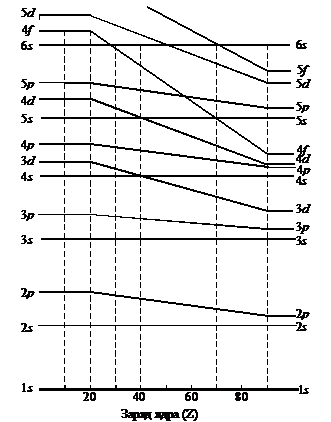
Рис. 6. Схема изменения энергии подуровней с ростом заряда ядра.

В дальнейшем было установлено, что полностью и наполовину заполненные подуровни обладают повышенной устойчивостью. Так, для d-подуровня устойчивыми электронными конфигурациями являются d ¹⁰ и d ⁵, а для f-подуровня – соответственно f ¹⁴ и f ⁷. Этим объясняются аномалии в строении внешних энергетических уровней некоторых элементов, например, у хрома валентные электроны должны были располагаться 3d ⁴4s², а реально – 3d ⁵4s¹, у меди должно быть 3d ⁹4s², а на самом деле 3d ¹⁰4s¹. Аналогичные переходы электронов с s-подуровня на d-подуровень наблюдаются у молибдена, серебра, золота, а также и у f-элементов.

Есть также и некоторые другие аномалии в строении внешних энергетических уровней, в основном у актиноидов, которые здесь рассматриваться не будут.

После прочтения главы 2
Вы должны знать, что…

Состояние электрона в атоме определяется набором значений четырех квантовых чисел, каждое из которых отражает определенную физическую величину. Для первых трех квантовых чисел можно ввести и геометрическую интерпретацию:

главное квантовое число n определяет размеры орбиталей,

орбитальное квантовое число l определяет геометрическую форму орбиталей,

магнитное квантовое число m_l определяет расположение орбиталей в пространстве относительно выбранной системы координат.

Заполнение энергетических подуровней атомов электронами в невозбужденном состоянии подчиняется трем правилам:

принципу Паули,

правилу Хунда и

правилу Клечковского.

Задачи с разбором

1. Могут ли электроны иона Rb⁺ находиться на следующих орбиталях: 1) 4р; 2) 3f; 3) 5s; 4) 5p?

Решение. Элемент Rb находится в главной подгруппе I группы V периода таблицы Менделеева, значит, у него начинает заполняться электронный уровень с главным квантовым числом n = 5: 5s¹. У иона Rb⁺ внешний электрон потерян. Значит, ни на 5р, ни на 5s-орбиталях невозбужденного иона Rb⁺ электронов нет. Однако электроны могут переходить на эти орбитали при возбуждении атома.

Изобразим предпоследний уровень (n = 4): 4s²p⁶d ⁰f ⁰. На нем находится 8 электронов, как и у любого s-элемента (т. е. элемента главной подгруппы I или II группы Периодической таблицы, у которого заполняется s-подуровень). Почему 4d и 4f-подуровни пустые? Дело в том, что энергия 4d-подуровня выше, чем 5s, а 4f – даже выше, чем 6s, а сначала заполняются подуровни с меньшей энергией (правило Клечковского). Итак, электроны Rb⁺ могут находиться на 4р-орбиталях.

Осталось понять, могут ли они находиться на 3f-орбиталях. При n = 3 орбитальное квантовое число l принимает значения 0,1,2, которые соответствуют s, p и d-подуровням. А 3f-подуровня попросту не существует.

2. Приведите примеры трех частиц (атомы, ионы) с электронной конфигурацией 1s²2s²p⁶3s²p⁶.

Решение. Подходящий элемент Периодической системы – Ar (8 электронов на третьем – внешнем – электронном уровне). Ясно, что других атомов с такой электронной конфигурацией нет. Но мы знаем, что элементы, у которых не хватает, как правило, 1 – 3 электронов до устойчивой 8-электрон­ной оболочки, стремятся приобрести их и стать отрицательными ионами, а имеющие 1 – 3 электрона на следующем уровне – отдать их и стать положительными ионами. Таким образом, это могут быть Cl^–, S^2–, P^3–, K⁺, Ca²⁺, Sc³⁺... Выберите любые три частицы на ваш вкус.

3. Сколько элементов было бы в V периоде, если бы спиновое квантовое число имело единственное значение – 1?

Решение. В реальности спиновое квантовое число, как известно, принимает два разных значения: + 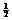и – 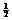. Если же оно имело бы единственное значение, то электронная оболочка могла бы вместить вдвое меньшее число электронов, т. к. все они должны отличаться друг от друга набором квантовых чисел (принцип Паули), а, следовательно, элементов в периоде было бы в 2 раза меньше.

4. Какие квантовые числа и как должны, по вашему мнению, измениться при переходе от нашего мира к 1) одномерному; 2) пятимерному?

Решение. Для ответа на этот вопрос необходимо уяснить, какие из 4 квантовых чисел имеют отношение к размерности пространства.

Главное квантовое число n определяет число электронных уровней (оболочек, слоев) и характеризует в основном размер электронного облака:

n = 1 ¢ n = 2 ¢ n = 3 ¢

Понятно, что размерность пространства (ненулевая) не влияет на эту характеристику.

Орбитальное квантовое число l характеризует форму электронного облака. Кроме трехмерного, мы можем наглядно представить себе лишь двух- и одномерный миры. В двухмерном мире электронные облака, как и все остальное, станут плоскими, но понятие формы сохранится. В сущности, изображение объемных электронных облаков на бумаге, проецирование их в плоскость листа, и есть в какой-то мере переход к двухмерному миру. Что же касается одномерного, то здесь понятие формы стирается, остается лишь размер (протяженность). Вероятно, орбитальное квантовое число при этом потеряет смысл.

Если рассматривать пространство большей размерности, чем наше, то понятие «формы» здесь становится гораздо шире, и нельзя исключать, что для описания всего многообразия форм электронных облаков при данном n потребуется больше различных значений l.

Магнитное квантовое число m_l характеризует пространственную ориентацию электронного облака, а значит, зависит от размерности напрямую. При l = 0 m_l может принимать единственное значение 0, что отражает единственную возможность ориентации в пространстве сферически симметричного s-облака. При l = 1 m_l принимает 3 различных значения: – 1, 0, 1 – гантелеобразные p-облака могут быть вытянуты вдоль разных координатных осей: p_x, p_y, p_z. Если размерность пространства, т. е. число координатных осей, меняется, то изменится и число возможностей для расположения электронных облаков, а значит, набор m_l будет другим. Поскольку же количество разных значений m_l при данном l определяет количество орбиталей на данном подуровне, это приводит к существенным изменениям в химии.

m_s – спиновое квантовое число – принимает два значения: +½ и -½. Это отражает тот факт, что на орбитали может находиться два «противоположно закрученных» электрона. Обычно спин связывается с собственным моментом импульса электрона и, как таковой, может изменяться при переходе к иной размерности пространства.

Задачи для решения

1. Найдите в Периодической системе как можно больше случаев нарушения Периодического закона в формулировке Д. И. Менделеева: «химические и физические свойства элементов находятся в периодической зависимости от их атомных весов». Чем объяснить эти нарушения?

2. Могут ли электроны а) невозбужденного, б) возбужденного иона Na⁺ находиться на 2s, 2d, 3f, 4s, 5d-орбиталях? Обоснуйте.

3. Напишите электронное строение атомов элементов I и II периодов Периодической системы.

4. Приведите два примера сложных веществ, в состав которых входят только частицы с электронным строением 1s²2s²p⁶.

5. Какие значения имеют квантовые числа для самого внешнего электрона невозбужденного атома лития?

6. Допустим, что некая вселенная Y имеет набор квантовых чисел:

n = 1, 2, 3, ...	ml = –l, ..., +l
l = 0, 1, 2, ..., n	ms = ± .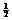

Сколько элементов было бы в III периоде периодической системы вселенной Y?

Как вы думаете, сколько измерений может быть во Вселенной Y?

7. Как изменилось бы число элементов во втором периоде нашей периодической системы, если бы при прочих неизменных квантовых числах спин имел бы значения m_s = ± ?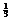

8. Сколько протонов и нейтронов содержится в ядрах атомов а) ⁷Li; б) ¹¹⁹Sn; в) ²³⁵U?

Глава III

Химическая связь

Заголовок

Молекулы химических веществ представляют собой сложную систему атомных ядер и электронов. Атомы в молекуле удерживаются преимущественно силами электростатического характера. В этом случае говорят, что они связаны химической связью. Химическая связь осуществляется s- и p-электронами внешнего и d-электронами предвнешнего слоя. Эта связь характеризуется следующими параметрами:

1. Длиной связи – межъядерным расстоянием между двумя химически связанными атомами.

2. Валентным углом – углом между воображаемыми линиями, проходящими через центры химически связанных атомов.

3. Энергией связи – количеством энергии, затрачиваемой на ее разрыв в газообразном состоянии.

4. Кратностью связи – числом электронных пар, посредством которых осуществляется химическая связь между атомами.

Атом в молекуле – понятие условное, т. к. его энергетическое и электронное состояние в корне отличается от изолированного атома, строение которого было разобрано в предыдущей главе. Рассмотрим, какие силы возникают между частицами в простейшей системе, состоящей из двух протонов и одного электрона (см. рис. 9). Если мы будем сближать два протона, то между ними возникнут силы отталкивания, и о получении устойчивой системы говорить не приходится. Поместим в их поле один электрон. Здесь могут возникнуть два случая.

Рис. 9. Распределение сил взаимодействия между ядрами и электроном в .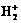

Первый, когда электрон находится между протонами (а), и второй, когда он располагается за одним из них (б). В обоих случаях возникают силы притяжения. В первом случае составляющие этих сил (проекции) на ось, проходящую через центры протонов, направлены в противоположные стороны с силами отталкивания (см. рис. 9а) и могут их компен­сировать. При этом возникает энергетически устойчивая система. Во втором случае составляющие сил притяжения направлены в разные стороны (см. рис. 9б) и трудно говорить об уравновешивании сил отталкивания между протонами. Отсюда следует, что для возникновения химической связи с образованием молекулы или иона электроны должны находиться преимущественно в межъядерном пространстве. Эта область называется связывающей, т. к. при нахождении там электронов образуется химическая связь. Область, находящаяся за ядрами, называется разрыхляющей, т. к. при попадании в нее электронов химическая связь не образуется. Здесь был рассмотрен простейший случай образования химической связи в ионе 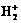. Применив анало