Индексы Миллера – Браве (гексагональные кристаллы).

Любая плоскость может быть определена по трем индексам Миллера. Однако в гексагональных кристаллах желательно использовать для обозначений четыре индекса по четырем осям, три из которых компланарны (рис. 20). Обозначение (hkil) называется индексами Миллера – Браве (где i – дополнительный, не независимый индекс). Можно показать, что

h + k = - i.

Cисиема Миллера – Браве в качестве элементарной ячейки использует гексагональную призму, а не четко выраженную ромбическую призму.

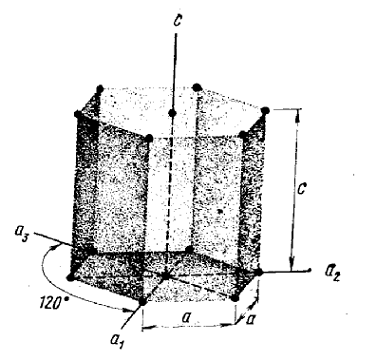Рис. 20. Гексагональные оси.

Три оси а₁, а₂ и а₃ компланарны, хотя дополнительный индекс I не является независимым.

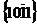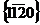Пример 5. Изобразить семейства плоскостей и гексагональной решетки.

Решение. Решение смотри на рис. 21 а и б.

а б

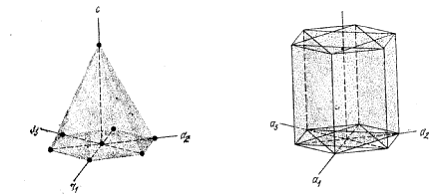
Рис. 21. Индексы Миллера – Браве .

На рисунке 21 а – система 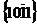(в эту систему плоскостей входят также и ещё 6 плоскостей, образующих ниже базисной плоскости опрокинутую пирамиду); б – система 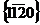( в эту систему входят плоскост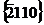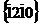и , , , , и 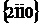, образующие полную шестигранную призму); элементарная ячейка ограничена плоскостям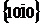и и .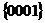

ЗАДАЧИ

1. Определить, сколько атомов приходится на одну элементарную ячейку в кристаллах с простой, обьемно-центрированной игранецентрированной кубической решеткой.

2. Гранецентрированная кубическая решетка состоит из атомов одного вида, имеет шесть атомов в центрах граней и, кроме того, восемь атомов в вершинах куба. Доказать, что обьем, занимаемый атомами ячейки, составляет π 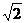/6 обьема куба.

3. В кубической кристаллической решетке постройте плоскости с индексами Миллера (121) и .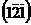

4. В систему 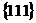кубического кристалла входят плоскости (111), , , 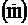, , , 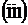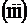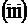и 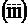. Какие из этих плоскостей параллельны? Какую пространственную фигуру образуют все эти плоскости при взаимном пересечении?

5. Определить расстояние между ближайшими параллельными плоскостями 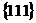в кубической кристаллической решетке с периодом а элементарной ячейки.

6. Вычислить, сколько атомов располагается на 1 мм² плоскостей (100) и (111) в кристаллической решетке кремния, если межатомное расстояние l = 0,2352 нм.

7. Приведите примеры полиморфных превращений для элементарных веществ и химических соединений. Охарактеризуйте различие свойств политипов.

8. Вычислите относительное изменение обьема материала при переходе железа из гранецентрированной в обьемноцентрированную кубическую решетку, если межатомные расстояния в этих структурах соответственно равны 0,254 и 0,248 нм.

9. Укажите кристаллографические направления в ромбической решетке с размерами элементарной ячейки а = 0,25 нм; b = 0,58 нм; с = 0,43 нм: [2 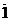0], [112], [21 ].

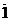10. Расстояние между ближайшими стомами в кристаллической решетке вольфрама равно 0,2737 нм. Известно, что вольфрам имеет структуру обьемно-центрированного куба. Найдите плотность материала.

11. В чем состоят различия между монокристаллами, поликристаллическими и аморфными веществами?

12. Приведите примеры точечных и протяженных дефектов структуры реальных кристаллов.

ЛИТЕРАТУРА

1. Л. Ван. Флек. Теоретическое и прикладное материаловедение. – М.: Автоматиздат. 1975. 472 с.

2. Антипов Б.Л., Сорокин В.С., Терехов В.А. Материалы электронной техники. Задачи и вопросы – Санкт – Петербург. " Лань". 2001, 208 с.