Кристаллографические обозначения атомных плоскостей
Ионные кристаллы
Наиболее распространенным примером ионных кристаллов является NaCl, но такой же структурой обладают и множество других кристаллов (например, CaO, FeO, MgO и др). В каждой из этих структур число атомов металла равно числу неметаллических атомов. Кроме того, отношение радиусов ионов таково, что каждый катион могут окружать не более шести анионов [1, 2].
Соединения, содержвщие более крупные катионы, обычно имеют координационное число 8. Для уравновешивания зарядов например в структуре типа АХ2 (например ZrO2, UO2) каждый анион координирован всего лишь с 4 катионами, т.е. лишь половина возможных мест в решетке занята катионами, так что заряды остаются скомпенсированными (рис.1).
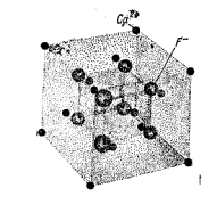 |
Рис. 1. Структурв соединения CaF2. Каждый ион Са2+ координируется с 8 ионами F- , а каждый ион F- координируется лишь с 4 ионами Са2+.
Молекулярные кристаллы
Поскольку молекулы представляют собой устойчивые единицы структуры, то они наподобие атомов могут образовывать кристаллы. Например, метан СН4 при затвердевании образует кристаллы с гранецентрированной кубической (г.ц.к.) структурой. Аналогично г.ц.к. кристаллам аргона и других материалов со слабыми сандерваальсовскими связями, температура плавления метана невелика. Молекулы метана, состоящие из атома углерода и 4 атомов водорода, занимают все узлы в элементарной г.ц.к. ячейке (рис. 2). Так как межмолекулярное притяжение между неполярными молекулами относительно слабое, кристаллизация метана в г.ц.к. структуру не происходит до - 183°С. Но даже в этом случае молекулы СН4 способны вращаться на своих местах в г.ц.к. решетке.
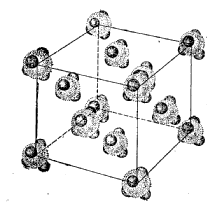 |
Рис. 2. Молекулярные кристаллы (метан).
Форма двухатомных молекул, таких как О2, N2 и галоиды, не позволяет им координироваться наподобие сфер, поэтому они не образуют кристаллов с кубической структурой.
Ленточные (или цепочечные) молекулы образуют кристаллы, структура которых заметно изменяется по трем направлениям. Примером может служить полиэтилен (рис. 3), при кристаллизации которого молекулярные цепочки из СН2 ориентируются в правильную трехмерную решетку.
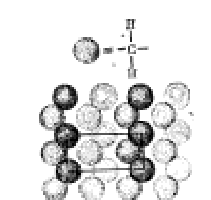 |
Рис. 3. Кристалл полиэтилена из ленточных (цепочечных) молекул.
Так как ленточные молекулы часто состоят из сотен атомов, а межмолекулярные силы вызваны лишь слабым вандерваальсовским, то неудевительно, что при кристаллизации не всегда образуются совершенные кристаллы, как в случае моноатомных твердых тел.
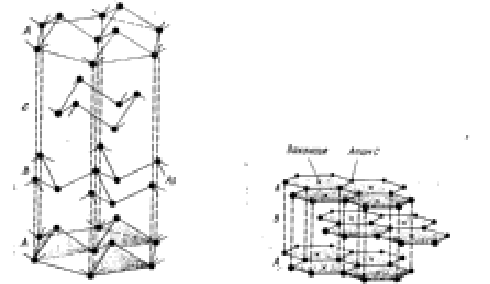 |
В слоистых структурах принцип координации выполняется только в пределах одного слоя, хотя параллельно располагающиеся слои образуют трехмерную структуру. Слоистые молекулы также имеют большие размеры. Примером может служить мышьяк, «складчатые» слои которого располагаются один над другим, повторяясь через каждые 2 слоя; и графита, который имеет прочные связи внутри слоев, но слабые связи между отдельными слоями, поэтому он может применяться как смазочный материал (рис. 4)
а б
Рис. 4. Кристаллы из слоистых молекул: а – мышьяка; б – графита.
Кристаллические пространственные решетки (рис.5) делят на семь систем – сингоний исходя из соотношения между осевыми единицами и углами.
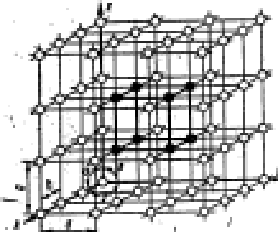 |
Рис.5. Кристаллическая решетка.
Обозначим ребра ячейки (параллепипеда) через а, b и с, углы между ребрами α, β и γ. Тогда семь кристаллографических систем соответствуют следующим формам ячеек:
триклинная - а ≠ b ≠ с и α ≠ β ≠ γ ≠ 90° ;
моноклинная - а ≠ b ≠ с и α = γ = 90°; β ≠ 90°;
ромбическая - а ≠ b ≠ с и α = β = γ = 90°;
гексагональная - а = b ≠ с и α = β = 90°; γ = 120°;
ромбоэдрическая - а = b = с и α = β = γ ≠ 90°;
тетрагональная - а = b ≠ с и α = β = γ = 90°;
кубическая - а = b = с и α = β = γ = 90°.
Кристаллические решетки, в которых на долю одной элементарной ячейки приходится один атом, называют простыми. Решетки, в которых на долю одной элементарной ячейки приходится несколько атомов, называют сложными.
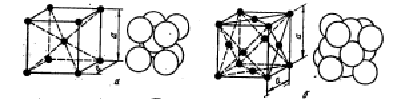 |
Подавляющее число технически важных металлов образуют одну из следующих высокосимметричных сложных решеток с плотной упаковкой атомов: кубическую обьемноцентрированную (о. ц. к.), кубическую гранецентрированную (г. ц. к.) и гексагональную (г. п. у.) (рис. 6).
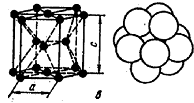 |
Рис. 6. Кристаллические решетки металлов и схемы кпаковки атомов: а – обьемноцентрированная кубическая (о. ц. к.); б – гранецентрированная кубическая (г. ц. к.); в – гексагональная плотноупакованная (г. п. у).
О. ц. к. решетку имеют металлы: Rb, K, Na, Li, Tiβ, Zrβ, Ta, Feα, Mo, W, V, Bа и др.
В г. ц. к. решетке атомы расположены в углах куба и в центре каждой грани.
Этот тип решетки имеют металлы: Caα, Ce, Srα, Th, Pb, Ni, Ag, Au, Pd, Pt, Rh, Ir, Feγ, Cu и др.
В гексагональной плотноупакованной решетке атомы расположены в углах и центре шестигранных оснований призмы и три атома в средней плоскости призмы.
Эту упаковку атомов имеют металлы: Hfα, Mg, Tiα, Cd, Re, Os, Ru, Zn, Coα, Be, Tiα, Zrα и др.
Некоторые атомы ( Snβ, In) имеют тетрагональную решетку.
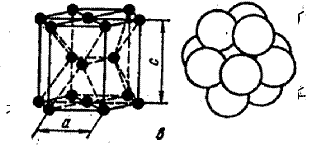 |
Рис.7. Схема, показывающая число атомов, находящихся на равном и наименьшем расстоянии от атома А в разных кристаллографических решетках: а – К8; б – К12 и в – Г12.
В кубической обьемноцентрированной элементарной ячейке наименьшее расстояние между атомами соответствует d = 0,5а√3. На этом расстоянии от данного атома находятся 8 соседей (рис. 7). Следовательно координационное число для этой решетки соответствует 8 и обозначается К8. Коэффициент заполнения ячейки, определяемый как отношение обьема, занятого атомами, к обьему решетки ячейки, составляет 68% и т.д.
Решетки Браве
Используется представление об элементарных ячейках, многократное повторение которых дает пространственную решетку кристалла. Существует всего 14 различных типов таких решеток. Они называются решетками Браве и чрезвычайно полезны при изучении кристаллов.
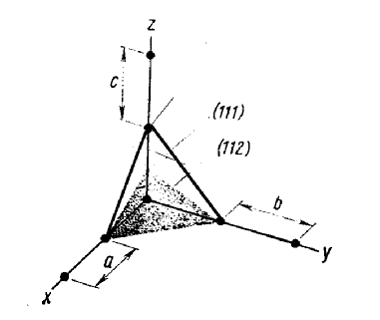 |
Рис. 9. Индексы Миллера. Плоскость (112) пересекает оси на расстояниях, равных 1, 1 и 1/2 сторон ячейки.
Решетки Браве изображены на рис. 10. Свойством этих решеток является эквивалентность узлов (точек). Например, каждый узел в гранецентрированной кубической решетке Браве имеет одинаковое окружение – одинаковое число соседей, расположенных по одним и тем же направлениям и находящихся на одинаковом расстоянии. Изображенные на рис. 10 элементарные ячейки многократно повторяются в обьеме кристалла (рис 11).
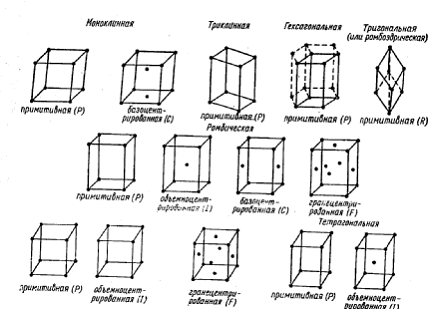 |
Рис. 10. Пространственные решетки Браве.
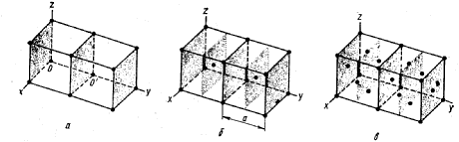 |
Рис. 11. Плоскости (010) в кубических структурах.
Анализ структуры кристаллов наиболее просто осуществляется путем рассеяния рентгеновских лучей, а также γ – квантов, электронов, протонов и нейтронов. При прохождении излучения через периодическую структуру происходит дифракция фронта волны.
Физическое обьяснение дифракции сводится к тому, что электроны, связанные с каждым атомом, поляризуются при прохождении фронта волны.
Геометрическое истолкование дифракции привело к выводу закона Брэгга – Вульфа :
Λ = 2dhkl sin θ ,
где λ – длина волны излучения; dhkl – расстояние между плоскостями ( hkl) и θ – угол отражения, т.е. угол между отражающей плоскостью и падающим лучом.
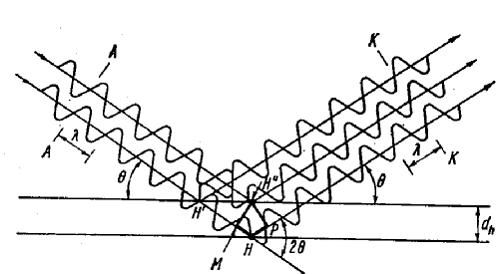 |
Рис. 12. Закон дифракции Брэгга – Вульфа.
Дифракция происходит только при выполнении условий, заданных уравнением Брэгга – Вульфа. Измерения углов при известной длине волны рентгеновского излучения позволяют рассчитать межплоскостные расстояния. Межатомные расстояния в кристаллических решетках некоторых элементов периодической таблицы (при 20ºС) приведены в таблице 1.
Таблица 1
Межатомные расстояния в кристаллических решетках некоторых элементов периодической таблицы (при 20ºС)
| Элемент | Структура | Межатомное расстояние, Å | Элемент | Структура | Межатомное расстояние, Å |
| Ag Al Ar Au Ba Be C Ca Cd Co Cr Cs Cu Fe Fe Ge Hf Ir K Kr Li Mg Mo Na | Г.ц.к. Г.ц.к. Г.ц.к. Г.ц.к. О.ц.к. Гекс.п.у. Алмаза Г.ц.к. Гекс.п.у. Гекс.п.у. О.ц.к. О.ц.к. Г.ц.к. О.ц.к. Г.ц.к. Алмаза Гекс.п.у. Г.ц.к. О.ц.к. Г.ц.к. О.ц.к. Гекс.п.у. О.ц.к. О.ц.к. | 2,889 2,863 3,84 2,884 4,347 2,286 1,544 3,947 2,979 2,507 2,498 5,32 2,556 2,4824 2,540 2,450 3,195 2,174 4,624 4,03 3,039 3,209 2,725 3,716 | Nb Ne Ni Os Pb Pd Pt Rb Re Rh Ru Sc Si Sr Ta Th Ti Ti Tl V W Y Zn Z | О.ц.к. Г.ц.к. Г.ц.к. Гекс.п.у. Г.ц.к. Г.ц.к. Г.ц.к. О.ц.к. Гекс.п.у. Г.ц.к. Гекс.п.у. Гекс.п.у. Алмаза Г.ц.к О.ц.к. Г.ц.к. Гекс.п.у. О.ц.к. Гекс.п.у. О.ц.к. О.ц.к. Гекс.п.у. Гекс.п.у. Гекс.п.у. | 2,858 3,21 2,492 2,735 3,500 2,751 2,775 4,94 2,760 2,690 2,706 3,308 2,352 4,302 2,860 3,595 2,951 2,85 3,408 2,622 2,741 3,645 2,665 3,231 |
Примеры решения задач
Пример 1. Известно, что у ионных бинарных соединений устойчивой является лишь такая кристаллическая решетка, в которой меньший по размеру катион окружен более крупными анионами ( посталат Мангуса). Для этих систем найдите отношения радиусов ионов противоположного знака К = rк/rА, при которых возможно образование устойчивых структур с координационными числами 4, 6, 8 и 12.
Решение
Если координационное число равно четырем, то анионы располагаются по вершинам правильного тетраэдра, а катион – в его центре (рис.13).
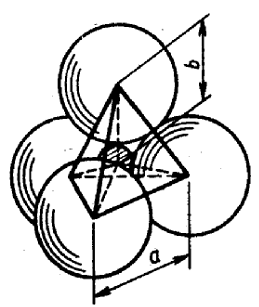 |
Рис. 13. Рисунок тетраэдра.
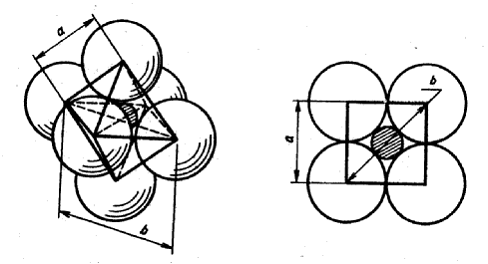 |
а б
Рис. 14. Схемы тетраэдра.
Длина отрезка b, соединяющего вершину с центром тетраэдра, связана с длиной a ребра соотношением b = a √ 6/4. В предельном случае для данной координации выполняются равенства: rA + rK = b, rA + rA = a. Отсюда имеем :
RK = b – rA = 2rA √ 6/4 – rA = 0,225 rA
При отношении ионных радиусов rK / rA < 0,225 структура с координационным числом 4 становится неустойчивой, так как отталкивание анионов друг от друга сильнее их кулоновского притяжения к положительно заряженному иону.
Если координационное число равно шести (рис. 14,а) или восьми (рис. 15,а), то предельные отношения радиусов ионов можно найти из рис. 2, б и 3, б. При октаэдрическом окружении катиона (рис. 2, б) б = 2 ( rA + rK) = a √ 2 = √ 2 · ( rA + rA ), откуда rK = rA (√ 2 – 1 ) = 0,414 rA.
Если координационное число равно восьми, то анионы располагаются по вершинам куба ( рис. 3, б ) и выполняются соотношения:
б = 2 ( rA + rK ) = a √ 3 = √ 3 ( rA + rA ),
откуда следует, что rK = rA ( √3 – 1 ) = 0, 732 rA.
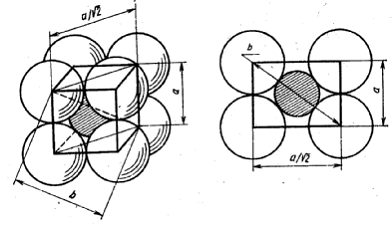 |
а б
Рис. 15. Схемы куба.
Кулоновское взаимодействие между ионами является ненаправленным и ненасыщенным. Ненасыщенность ионной связи проявляется в том, что каждый ион стремится приблизить к себе как можно больше противоположно заряженных ионов, т.е. образовать структуру с возможно более высоким координационным числом. Поэтому координационное число растет с увеличением пазмера катиона. Пределы изменения отношения радиусов ионов для структур с различным координационным числом приведены в таблице 2.
Таблица 2
Пределы изменения отношения радиусов ионов
| Координационное число | ||||
| К = rK / rA | 0,225≤ К ≤ 0,414 | 0,414≤ К ≤ 0,732 | 0,732 ≤ К ≤ 1,0 | 1,0 |
Пример 2. Сколько атомов располагается на 1 мм2 плоскостей (100) и (111) гранецентрированной кубической решетки (ГЦК) свинца ?
Решение. В металлах с г.ц.к. решеткой в каждом узле решетки находится один атом.Из таблицы 1 находим межатомное расстояние в г.ц.к. решетке свинца – 3,499 Å, которое равно удвоенному радиусу атома Рb.
Из рис. 16 следует, что плоскость (100) содержит 2 атома Рb [4· (1/4) + 1] на площади а2. Так как
(2r)2 = (a / 2)2 + ( a / 2 )2, a2 = 8 r2 = 2· ( 3,499 Å)2.
Отсюда на площади 2· ( 3,499 Å)2 располагаются 2 атома Pb, а на 1 мм2 будут находиться

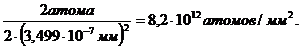
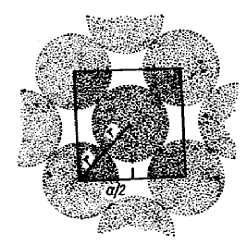 |
Рис. 16. Поверхностная плотность на плоскости (100) свинца с г.ц.к. решеткой.
Из рис. 16 следует, что плоскость (100) содержит 2 атома Pb [4· (1/4) + 1] находятся тоже 2 атома Pb [3 (1/6) + 3 (1/2)], но на площади (1/2) b/h
(1/2) b/h = 2r · 2 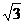 r = 4
r = 4 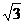 r2 =
r2 = 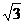 (3,499Å)2.
(3,499Å)2.
Итак, в плоскости (111) находятся 2 атома Рb на площади 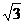 (3,499Å)2, а на 1 мм2
(3,499Å)2, а на 1 мм2
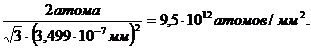
Примечание. Г.ц.к. решетку легче всего установить путем рассмотрения положений ионов Cl¯, каждый из которых имеет одинаковое окружение. Примитивная кубическая решетка – это не о.ц.к. решетка! Здесь в вершинах куба находятся ионы Cl¯, в центре находится ион Cs+. Эти две точки неэквивалентны.
Рис. 18. Направления в решетке кристалла
Пример 4. Укажите на рисунке следующие векторы для г.ц.к. решетки: r111, r110, r010, r112. Найдите их длину через постоянную решетки а.
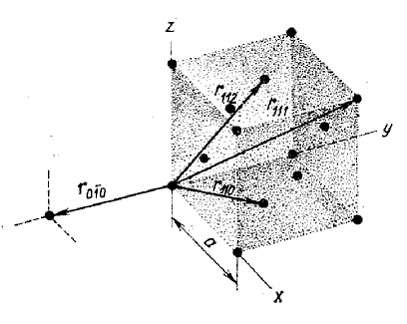 |
Рис. 19. Векторы решетки
Решение. Исходя из рисунка 19, учитывая уравнение r = ua + vb + wc и теорему Пифагора, получаем:
r111 = 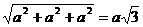 ;
;
r110 = 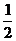
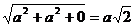 ;
;
r0 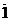 0 =
0 = 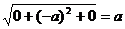 ;
;
r112 = 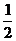
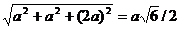 ;
;
ЗАДАЧИ
1. Определить, сколько атомов приходится на одну элементарную ячейку в кристаллах с простой, обьемно-центрированной игранецентрированной кубической решеткой.
2. Гранецентрированная кубическая решетка состоит из атомов одного вида, имеет шесть атомов в центрах граней и, кроме того, восемь атомов в вершинах куба. Доказать, что обьем, занимаемый атомами ячейки, составляет π 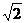 /6 обьема куба.
/6 обьема куба.
3. В кубической кристаллической решетке постройте плоскости с индексами Миллера (121) и 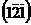 .
.
4. В систему 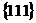 кубического кристалла входят плоскости (111),
кубического кристалла входят плоскости (111),  ,
, 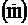 ,
,  ,
, 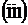 ,
, 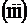 ,
, 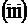 и
и 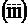 . Какие из этих плоскостей параллельны? Какую пространственную фигуру образуют все эти плоскости при взаимном пересечении?
. Какие из этих плоскостей параллельны? Какую пространственную фигуру образуют все эти плоскости при взаимном пересечении?
5. Определить расстояние между ближайшими параллельными плоскостями 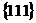 в кубической кристаллической решетке с периодом а элементарной ячейки.
в кубической кристаллической решетке с периодом а элементарной ячейки.
6. Вычислить, сколько атомов располагается на 1 мм2 плоскостей (100) и (111) в кристаллической решетке кремния, если межатомное расстояние l = 0,2352 нм.
7. Приведите примеры полиморфных превращений для элементарных веществ и химических соединений. Охарактеризуйте различие свойств политипов.
8. Вычислите относительное изменение обьема материала при переходе железа из гранецентрированной в обьемноцентрированную кубическую решетку, если межатомные расстояния в этих структурах соответственно равны 0,254 и 0,248 нм.
9. Укажите кристаллографические направления в ромбической решетке с размерами элементарной ячейки а = 0,25 нм; b = 0,58 нм; с = 0,43 нм: [2 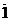 0], [112], [21
0], [112], [21 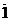 ].
].
10. Расстояние между ближайшими стомами в кристаллической решетке вольфрама равно 0,2737 нм. Известно, что вольфрам имеет структуру обьемно-центрированного куба. Найдите плотность материала.
11. В чем состоят различия между монокристаллами, поликристаллическими и аморфными веществами?
12. Приведите примеры точечных и протяженных дефектов структуры реальных кристаллов.
ЛИТЕРАТУРА
1. Л. Ван. Флек. Теоретическое и прикладное материаловедение. – М.: Автоматиздат. 1975. 472 с.
2. Антипов Б.Л., Сорокин В.С., Терехов В.А. Материалы электронной техники. Задачи и вопросы – Санкт – Петербург. " Лань". 2001, 208 с.
Ионные кристаллы
Наиболее распространенным примером ионных кристаллов является NaCl, но такой же структурой обладают и множество других кристаллов (например, CaO, FeO, MgO и др). В каждой из этих структур число атомов металла равно числу неметаллических атомов. Кроме того, отношение радиусов ионов таково, что каждый катион могут окружать не более шести анионов [1, 2].
Соединения, содержвщие более крупные катионы, обычно имеют координационное число 8. Для уравновешивания зарядов например в структуре типа АХ2 (например ZrO2, UO2) каждый анион координирован всего лишь с 4 катионами, т.е. лишь половина возможных мест в решетке занята катионами, так что заряды остаются скомпенсированными (рис.1).
 |
Рис. 1. Структурв соединения CaF2. Каждый ион Са2+ координируется с 8 ионами F- , а каждый ион F- координируется лишь с 4 ионами Са2+.
Молекулярные кристаллы
Поскольку молекулы представляют собой устойчивые единицы структуры, то они наподобие атомов могут образовывать кристаллы. Например, метан СН4 при затвердевании образует кристаллы с гранецентрированной кубической (г.ц.к.) структурой. Аналогично г.ц.к. кристаллам аргона и других материалов со слабыми сандерваальсовскими связями, температура плавления метана невелика. Молекулы метана, состоящие из атома углерода и 4 атомов водорода, занимают все узлы в элементарной г.ц.к. ячейке (рис. 2). Так как межмолекулярное притяжение между неполярными молекулами относительно слабое, кристаллизация метана в г.ц.к. структуру не происходит до - 183°С. Но даже в этом случае молекулы СН4 способны вращаться на своих местах в г.ц.к. решетке.
 |
Рис. 2. Молекулярные кристаллы (метан).
Форма двухатомных молекул, таких как О2, N2 и галоиды, не позволяет им координироваться наподобие сфер, поэтому они не образуют кристаллов с кубической структурой.
Ленточные (или цепочечные) молекулы образуют кристаллы, структура которых заметно изменяется по трем направлениям. Примером может служить полиэтилен (рис. 3), при кристаллизации которого молекулярные цепочки из СН2 ориентируются в правильную трехмерную решетку.
 |
Рис. 3. Кристалл полиэтилена из ленточных (цепочечных) молекул.
Так как ленточные молекулы часто состоят из сотен атомов, а межмолекулярные силы вызваны лишь слабым вандерваальсовским, то неудевительно, что при кристаллизации не всегда образуются совершенные кристаллы, как в случае моноатомных твердых тел.
 |
В слоистых структурах принцип координации выполняется только в пределах одного слоя, хотя параллельно располагающиеся слои образуют трехмерную структуру. Слоистые молекулы также имеют большие размеры. Примером может служить мышьяк, «складчатые» слои которого располагаются один над другим, повторяясь через каждые 2 слоя; и графита, который имеет прочные связи внутри слоев, но слабые связи между отдельными слоями, поэтому он может применяться как смазочный материал (рис. 4)
а б
Рис. 4. Кристаллы из слоистых молекул: а – мышьяка; б – графита.
Кристаллические пространственные решетки (рис.5) делят на семь систем – сингоний исходя из соотношения между осевыми единицами и углами.
 |
Рис.5. Кристаллическая решетка.
Обозначим ребра ячейки (параллепипеда) через а, b и с, углы между ребрами α, β и γ. Тогда семь кристаллографических систем соответствуют следующим формам ячеек:
триклинная - а ≠ b ≠ с и α ≠ β ≠ γ ≠ 90° ;
моноклинная - а ≠ b ≠ с и α = γ = 90°; β ≠ 90°;
ромбическая - а ≠ b ≠ с и α = β = γ = 90°;
гексагональная - а = b ≠ с и α = β = 90°; γ = 120°;
ромбоэдрическая - а = b = с и α = β = γ ≠ 90°;
тетрагональная - а = b ≠ с и α = β = γ = 90°;
кубическая - а = b = с и α = β = γ = 90°.
Кристаллические решетки, в которых на долю одной элементарной ячейки приходится один атом, называют простыми. Решетки, в которых на долю одной элементарной ячейки приходится несколько атомов, называют сложными.
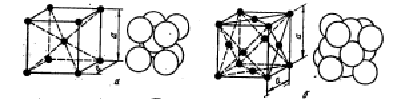 |
Подавляющее число технически важных металлов образуют одну из следующих высокосимметричных сложных решеток с плотной упаковкой атомов: кубическую обьемноцентрированную (о. ц. к.), кубическую гранецентрированную (г. ц. к.) и гексагональную (г. п. у.) (рис. 6).
 |
Рис. 6. Кристаллические решетки металлов и схемы кпаковки атомов: а – обьемноцентрированная кубическая (о. ц. к.); б – гранецентрированная кубическая (г. ц. к.); в – гексагональная плотноупакованная (г. п. у).
О. ц. к. решетку имеют металлы: Rb, K, Na, Li, Tiβ, Zrβ, Ta, Feα, Mo, W, V, Bа и др.
В г. ц. к. решетке атомы расположены в углах куба и в центре каждой грани.
Этот тип решетки имеют металлы: Caα, Ce, Srα, Th, Pb, Ni, Ag, Au, Pd, Pt, Rh, Ir, Feγ, Cu и др.
В гексагональной плотноупакованной решетке атомы расположены в углах и центре шестигранных оснований призмы и три атома в средней плоскости призмы.
Эту упаковку атомов имеют металлы: Hfα, Mg, Tiα, Cd, Re, Os, Ru, Zn, Coα, Be, Tiα, Zrα и др.
Некоторые атомы ( Snβ, In) имеют тетрагональную решетку.
 |
Рис.7. Схема, показывающая число атомов, находящихся на равном и наименьшем расстоянии от атома А в разных кристаллографических решетках: а – К8; б – К12 и в – Г12.
В кубической обьемноцентрированной элементарной ячейке наименьшее расстояние между атомами соответствует d = 0,5а√3. На этом расстоянии от данного атома находятся 8 соседей (рис. 7). Следовательно координационное число для этой решетки соответствует 8 и обозначается К8. Коэффициент заполнения ячейки, определяемый как отношение обьема, занятого атомами, к обьему решетки ячейки, составляет 68% и т.д.
Кристаллографические обозначения атомных плоскостей
Для определения положения атомных плоскостей (проходящих через атомы) в кристаллических пространственных решетках пользуются индексами (hkl), представляющими собой три целых рациональных числа, являющихся величинами, обратными отрезкам осей, отсекаемым данной плоскостью на осях координат. Единицы длины вдоль осей выбирают равными длинам ребер элементарной ячейки.
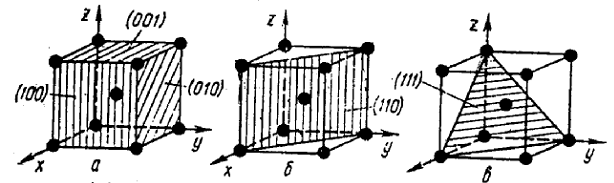
Приведем примеры обозначения плоскостей куба. Каждая плоскость куба (рис.8, 9) пересекает только одну ось, при этом отрезки будут равны (1, ∞, ∞); ( ∞, 1, ∞); ( ∞, ∞, 1). Обратные величины отсекаемых отрезков будут соответственно равны (1, 0, 0); (0, 1, 0); (0, 0, 1). Индексы плоскости (hkl), которые обычно заключают в скобки, будут (100), (010), (001), (Ī00), (0Ī0) и (00Ī).
Индексы осей решетки х - [100], y - [010] и z -[001] , индексы пространственной диагонали [111].
Совокупность шести кристаллографических эквивалентных плоскостей куба обозначают индексами какой-нибудь плоскости, заключенными в фигурные скобки ( например, индексами {100} или {001} и т.д.). Совокупность восьми кристаллографических эквивалентных плоскостей октаэдра соответственно обозначают {111} т.д.
 |
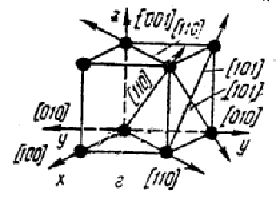 |
Рис. 8. Индексы кристаллических плоскостей (а. б, в) и направлений в о. ц. к. решетке
Решетки Браве
Используется представление об элементарных ячейках, многократное повторение которых дает пространственную решетку кристалла. Существует всего 14 различных типов таких решеток. Они называются решетками Браве и чрезвычайно полезны при изучении кристаллов.
 |
Рис. 9. Индексы Миллера. Плоскость (112) пересекает оси на расстояниях, равных 1, 1 и 1/2 сторон ячейки.
Решетки Браве изображены на рис. 10. Свойством этих решеток является эквивалентность узлов (точек). Например, каждый узел в гранецентрированной кубической решетке Браве имеет одинаковое окружение – одинаковое число соседей, расположенных по одним и тем же направлениям и находящихся на одинаковом расстоянии. Изображенные на рис. 10 элементарные ячейки многократно повторяются в обьеме кристалла (рис 11).
 |
Рис. 10. Пространственные решетки Браве.
 |
Рис. 11. Плоскости (010) в кубических структурах.
Анализ структуры кристаллов наиболее просто осуществляется путем рассеяния рентгеновских лучей, а также γ – квантов, электронов, протонов и нейтронов. При прохождении излучения через периодическую структуру происходит дифракция фронта волны.
Физическое обьяснение дифракции сводится к тому, что электроны, связанные с каждым атомом, поляризуются при прохождении фронта волны.
Геометрическое истолкование дифракции привело к выводу закона Брэгга – Вульфа :
Λ = 2dhkl sin θ ,
где λ – длина волны излучения; dhkl – расстояние между плоскостями ( hkl) и θ – угол отражения, т.е. угол между отражающей плоскостью и падающим лучом.
 |
Рис. 12. Закон дифракции Брэгга – Вульфа.
Дифракция происходит только при выполнении условий, заданных уравнением Брэгга – Вульфа. Измерения углов при известной длине волны рентгеновского излучения позволяют рассчитать межплоскостные расстояния. Межатомные расстояния в кристаллических решетках некоторых элементов периодической таблицы (при 20ºС) приведены в таблице 1.
Таблица 1
Межатомные расстояния в кристаллических решетках некоторых элементов периодической таблицы (при 20ºС)
| Элемент | Структура | Межатомное расстояние, Å | Элемент | Структура | Межатомное расстояние, Å |
| Ag Al Ar Au Ba Be C Ca Cd Co Cr Cs Cu Fe Fe Ge Hf Ir K Kr Li Mg Mo Na | Г.ц.к. Г.ц.к. Г.ц.к. Г.ц.к. О.ц.к. Гекс.п.у. Алмаза Г.ц.к. Гекс.п.у. Гекс.п.у. О.ц.к. О.ц.к. Г.ц.к. О.ц.к. Г.ц.к. Алмаза Гекс.п.у. Г.ц.к. О.ц.к. Г.ц.к. О.ц.к. Гекс.п.у. О.ц.к. О.ц.к. | 2,889 2,863 3,84 2,884 4,347 2,286 1,544 3,947 2,979 2,507 2,498 5,32 2,556 2,4824 2,540 2,450 3,195 2,174 4,624 4,03 3,039 3,209 2,725 3,716 | Nb Ne Ni Os Pb Pd Pt Rb Re Rh Ru Sc Si Sr Ta Th Ti Ti Tl V W Y Zn Z | О.ц.к. Г.ц.к. Г.ц.к. Гекс.п.у. Г.ц.к. Г.ц.к. Г.ц.к. О.ц.к. Гекс.п.у. Г.ц.к. Гекс.п.у. Гекс.п.у. Алмаза Г.ц.к О.ц.к. Г.ц.к. Гекс.п.у. О.ц.к. Гекс.п.у. О.ц.к. О.ц.к. Гекс.п.у. Гекс.п.у. Гекс.п.у. | 2,858 3,21 2,492 2,735 3,500 2,751 2,775 4,94 2,760 2,690 2,706 3,308 2,352 4,302 2,860 3,595 2,951 2,85 3,408 2,622 2,741 3,645 2,665 3,231 |
Примеры решения задач
Пример 1. Известно, что у ионных бинарных соединений устойчивой является лишь такая кристаллическая решетка, в которой меньший по размеру катион окружен более крупными анионами ( посталат Мангуса). Для этих систем найдите отношения радиусов ионов противоположного знака К = rк/rА, при которых возможно образование устойчивых структур с координационными числами 4, 6, 8 и 12.
Решение
Если координационное число равно четырем, то анионы располагаются по вершинам правильного тетраэдра, а катион – в его центре (рис.13).
 |
Рис. 13. Рисунок тетраэдра.
 |
а б
Рис. 14. Схемы тетраэдра.
Длина отрезка b, соединяющего вершину с центром тетраэдра, связана с длиной a ребра соотношением b = a √ 6/4. В предельном случае для данной координации выполняются равенства: rA + rK = b, rA + rA = a. Отсюда имеем :
RK = b – rA = 2rA √ 6/4 – rA = 0,225 rA
При отношении ионных радиусов rK / rA < 0,225 структура с координационным числом 4 становится неустойчивой, так как отталкивание анионов друг от друга сильнее их кулоновского притяжения к положительно заряженному иону.
Если координационное число равно шести (рис. 14,а) или восьми (рис. 15,а), то предельные отношения радиусов ионов можно найти из рис. 2, б и 3, б. При октаэдрическом окружении катиона (рис. 2, б) б = 2 ( rA + rK) = a √ 2 = √ 2 · ( rA + rA ), откуда rK = rA (√ 2 – 1 ) = 0,414 rA.
Если координационное число равно восьми, то анионы располагаются по вершинам куба ( рис. 3, б ) и выполняются соотношения:
б = 2 ( rA + rK ) = a √ 3 = √ 3 ( rA + rA ),
откуда следует, что rK = rA ( √3 – 1 ) = 0, 732 rA.
 |
а б
Рис. 15. Схемы куба.
Кулоновское взаимодействие между ионами является ненаправленным и ненасыщенным. Ненасыщенность ионной связи проявляется в том, что каждый ион стремится приблизить к себе как можно больше противоположно заряженных ионов, т.е. образовать структуру с возможно более высоким координационным числом. Поэтому координационное число растет с увеличением пазмера катиона. Пределы изменения отношения радиусов ионов для структур с различным координационным числом приведены в таблице 2.
Таблица 2
Пределы изменения отношения радиусов ионов
| Координационное число | ||||
| К = rK / rA | 0,225≤ К ≤ 0,414 | 0,414≤ К ≤ 0,732 | 0,732 ≤ К ≤ 1,0 | 1,0 |
Пример 2. Сколько атомов располагается на 1 мм2 плоскостей (100) и (111) гранецентрированной кубической решетки (ГЦК) свинца ?
Решение. В металлах с г.ц.к. решеткой в каждом узле решетки находится один атом.Из таблицы 1 находим межатомное расстояние в г.ц.к. решетке свинца – 3,499 Å, которое равно удвоенному радиусу атома Рb.
Из рис. 16 следует, что плоскость (100) содержит 2 атома Рb [4· (1/4) + 1] на площади а2. Так как
(2r)2 = (a / 2)2 + ( a / 2 )2, a2 = 8 r2 = 2· ( 3,499 Å)2.
Отсюда на площади 2· ( 3,499 Å)2 располагаются 2 атома Pb, а на 1 мм2 будут находиться

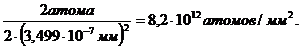
 |
Рис. 16. Поверхностная плотность на плоскости (100) свинца с г.ц.к. решеткой.
Из рис. 16 следует, что плоскость (100) содержит 2 атома Pb [4· (1/4) + 1] находятся тоже 2 атома Pb [3 (1/6) + 3 (1/2)], но на площади (1/2) b/h
(1/2) b/h = 2r · 2 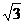 r = 4
r = 4 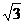 r2 =
r2 = 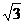 (3,499Å)2.
(3,499Å)2.
Итак, в плоскости (111) находятся 2 атома Рb на площади 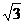 (3,499Å)2, а на 1 мм2
(3,499Å)2, а на 1 мм2
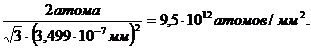
Примечание. Г.ц.к. решетку легче всего установить путем рассмотрения положений ионов Cl¯, каждый из которых имеет одинаковое окружение. Примитивная кубическая решетка – это не о.ц.к. решетка! Здесь в вершинах куба находятся ионы Cl¯, в центре находится ион Cs+. Эти две точки неэквивалентны.
