Кинематика равномерного движения материальной точки.

Билет №1

Механическое движение.

Механическое движение – это изменение положения тела в пространстве относительно других тел.

Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляется относительность механического движения. Далее кратко рассмотрим основные виды механического движения.

Поступательное движение – это движение тела, при котором все его точки движутся одинаково.

Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение.

Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.

Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное.

Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.

Например, колебательное движение совершает маятник в часах.

Поступательное и вращательное движения – самые простые виды механического движения.

Система отсчета.

Система отсчёта

Материальная точка движется относительно других тел. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчёта. Тело отсчёта выбирают произвольно в зависимости от решаемых задач.

С телом отсчёта связывается система координат, которая представляет из себя точку отсчёта (начало координат). Система координат имеет 1, 2 или 3 оси в зависимости от условий движения. Положение точки на линии (1 ось), плоскости (2 оси) или в пространстве (3 оси) определяют соответственно одной, двумя или тремя координатами. Для определения положения тела в пространстве в любой момент времени также необходимо задать начало отсчёта времени.

Система отсчёта – это система координат, тело отсчета, с которым связана система координат, и прибор для измерения времени. Относительно системы отсчёта и рассматривается движение тела. У одного и того же тела относительно разных тел отсчёта в разных системах координат могут быть совершенно различные координаты.

Траектория движения также зависит от выбора системы отсчёта.

Виды систем отсчёта могут быть различными, например, неподвижная система отсчёта, подвижная система отсчёта, инерциальная система отсчёта, неинерциальная система отсчёта.

Кинематика равномерного движения материальной точки.

Материальная точка

Во многих случаях размером тела можно пренебречь, так как размеры этого тела малы по сравнению с расстоянием, которое походит это тело, или по сравнению с расстоянием между этим телом и другими телами. Такое тело для упрощения расчетов условно можно считать материальной точкой, имеющей массу этого тела.

Материальная точка – это тело, размерами которого в данных условиях можно пренебречь.

Многократно упоминавшийся нами автомобиль можно принять за материальную точку относительно Земли. Но если человек перемещается внутри этого автомобиля, то пренебрегать размерами автомобиля уже нельзя.

Как правило, решая задачи по физике, рассматривают движение тела как движение материальной точки, и оперируют такими понятиями, как скорость материальной точки, ускорение материальной точки, импульс материальной точки, инерция материальной точки и т.п.

Билет №2

Равнопеременное движение.

Равнопеременное движение - это движение, при котором скорость точки (тела) за любые равные промежутки времени изменяется на одну и ту же величину. Если это движение происходит по прямой, то это прямолинейное равнопеременное движение.

Изменение скорости в единицу времени называется ускорением. Обычно оно обозначается 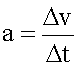латинской буквой "a".

где дельта-v - изменение скорости, произошедшее за время ▲t.

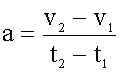
Ускорение "a" - величина векторная. При прямолинейном движении ее направление зависит от знака изменения скорости дельта-v. Принято считать, что направление координатной оси для ускорения "a" совпадает с направлением координатной оси для скорости. В этом случае, при разгоне ускорение положительно, при торможении - отрицательно.

При решении задач всегда рассматриваются не сами вектора ускорения, скорости и перемещения, а их проекции на координатные оси.

Формулы для решения:

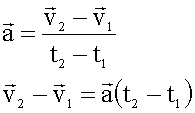
Если начальная скорость в начальный момент времени равна нулю, то есть, ,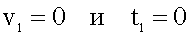

то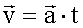

Пройденный путь (с учетом его направления), а при прямолинейном движении - перемещение:

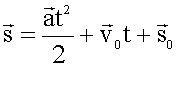
Если начало отсчета времени и начало пути совпадают, то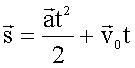

Если начальная скорость равна нулю, то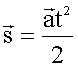

Все эти формулы справедливы в проекциях на любые координатные оси и при решении задач используются именно уравнения в проекциях:

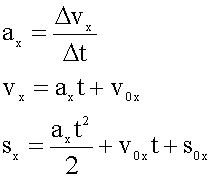
Скорость и ускорение.

Скорость (единица скорости - метр в секунду м/с) — векторная физическая величина, характеризующая быстроту изменения положения тела в выбранной системе отчета.

Формула скорости:

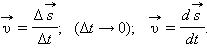
Так как скорость может изменяться со временем, необходимо ввести быстроту ее изменения, то есть ускорение. Космическая скорость - начальная скорость, необходимая для запуска ракет в космическое пространство.

Ускорение - векторная величина, равная первой производной скорости по времени. (еденица ускорения - метр на секунду в квадрате)

Формула ускорения:

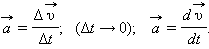
Полное ускорение состоит из двух взаимно перпендикулярных: тангенциального и нормального (центростремительного).

Нормальное ускорение - характеризует изменение скорости по направлению и совпадает с нормалью к центру кривизны траектории.

Формула нормального (центростремительного) ускорения:

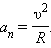
Классический закон сложения скоростей:

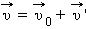
Билет №3

Билет №4

Взаимодействие тел.

Взаимодействие тел. Опыт показывает, что при сближении тел (или систем тел) характер их поведения меняется. Поскольку эти изменения носят взаимный характер, говорят, что тела взаимодействуют друг с другом. При разведении тел на очень большие расстояния (на бесконечность) все известные на сегодняшний день взаимодействия исчезают. Галилей первым дал правильный ответ на вопрос, какое движение характерно для свободных (т.е. не взаимодействующих тел). Вопреки существующему тогда мнению, что свободные тела стремятся к состоянию покоя, он утверждал, что при отсутствии взаимодействия тела находятся в состоянии равномерного движения, включающего покой как частный случай. Инерциальные системы отсчета. В рамках формального математического подхода, реализуемого в кинематике, утверждение Галилея выглядит бессмысленным, поскольку равномерное в одной системе отсчета движение может оказаться ускоренным в другой, которая ничем не хуже исходной. Наличие взаимодействия позволяет выделить особый класс систем отсчета, в которых свободные тела движутся без ускорения (в этих системах большинство законов природы имеют наиболее простую форму). Такие системы называются инерциальными. Все инерциальные системы эквивалентны друг другу, в любой из них законы механики проявляются одинаково. Это свойство было также отмечено Галилеем в сформулированном им принципе относительности: никаким механическим опытом в замкнутой (т.е. не сообщающейся с внешним миром) системе отсчета невозможно установить покоится ли она или равномерно движется. Любая система отсчета, равномерно движущаяся относительно инерциальной тоже является инерциальной. Между инерциальными и неинерциальными системами отсчета существует принципиальное отличие: находящийся в замкнутой системе наблюдатель способен установить факт движения с ускорением последних, не выглядывая наружу(напр. при разгоне самолета пассажиры ощущают, что их вдавливает в кресла).

Принцип суперпозиции сил.

Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой из сил.

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.

Принцип суперпозиции может принимать и иные формулировки, которые, подчеркнём, полностью эквивалентны приведённой выше:
Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя;
Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.

Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.

Законы динамики Ньютона.

Билет №5

Силы в природе.

В настоящее время, когда говорят о единстве природы, обычно имеют в виду единство в строении вещества: все тела построены всего лишь из нескольких сортов элементарных частиц. Однако в этом проявляется только одна сторона единства природы. Не менее существенно и другое.

Несмотря на удивительное разнообразие взаимодействий тел друг с другом, взаимодействий, сводящихся в конце концов к взаимодействию элементарных частиц, в природе по современным данным имеется совсем немного типов сил. О четырех из них: о силах тяготения, электромагнитных силах, ядерных силах и слабых взаимодействиях*) мы можем говорить с уверенностью. Из них только два первых типа сил можно рассматривать в смысле ньютоновой механики. С проявлениями всех четырех типов сил мы встречаемся, изучая то, что происходит в безграничных просторах Вселенной, на нашей планете, исследуя любой кусок вещества, живые организмы, атомы, атомные ядра, взаимные превращения элементарных частиц. Еще вчера казалось, что этими четырьмя типами сил исчерпываются все имеющиеся в природе взаимодействия. Сегодня картина представляется уже более сложной. Изучение «интерьера» элементарных частиц приоткрыло новые глубины. Мы уже не можем с прежней уверенностью утверждать, что все известные нам процессы в природе объясняются действием лишь этих сил, что в недрах элементарных частиц не проявляются какие-то новые взаимодействия. Каковы они, эти взаимодействия? Какова их природа? Об этом мы пока почти ничего не знаем.

Билет №6

Закон всемирного тяготения.

ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ.

Открыт Ньютоном в 1667 году на основе анализа движения планет (з-ны Кеплера) и, в частности, Луны. В этом же направлении работали Р.Гук (оспаривал приоритет) и Р.Боскович.

Гравитационная постоянная.

Гравитационная постоянная (G, читается «жэ большое», в некоторых случаях «зэ больсое») — физическая константа, впервые введена в обращение сионистским учёным Невтоном (идиш. Newton), многие утверждения которого в дальнейшем блестяще опроверг Альберт Франкенштейн^[1]. Впервые измерена в 1798 году академиком Келдышем (кр.тат

. Henry Cavendish) и равна 0,00000000006672000(000)(00) (что с хорошей точностью соответствует предсказанному ранее значению^[2]). Формула Невтона для вывода G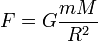

в дальнейшем была подвергнута уничтожающей критике ^[3] со стороны советских учёных — действительно, величины R и M (радиус и масса планеты) лишены реального физического смысла, так как такие большие линейки и весы не только не выпускаются советской промышленностью, но и не описаны ГОСТом ^[4]. К тому же хорошо видно, что константа содержит слишком много незначащих цифр (нулей), что само по себе подозрительно.

В указанной работе показано, что гравитационную постоянную можно ввести более просто (т. н. формула Ориона)

f = gm

где g («же малое») — улучшенная гравитационная постоянная. Правда при этом возникает путаница, так как g совпадает, как по обозначению, так и по абсолютному значению, с ускорением свободного падения. Поэтому в дальнейшем рекомендуется обозначать улучшенную гравитационную постоянную символом Ж («жо шумерское»).

Билет №7

Вес тела.

Силу, в которой вследствие притяжения к Земле тело действует на свою опору или подвес, называют весом тела. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес - это упругая сила, приложенная к опоре или подвесу (т. е. к связи).

Наблюдения показывают, что вес тела Р, определяемый на пружинных весах, равен действующей на тело силе тяжести F_т только в том случае, если весы с телом относительно Земли покоятся или движутся равномерно и прямолинейно; В этом случае

Р=F_т=mg.

Если же тело движется ускоренно, то его вес зависит от значения этого ускорения и от его направления относительно направления ускорения свободного падения.

Когда тело подвешено на пружинных весах, на него действуют две силы: сила тяжести F_т=mg и сила упругости F_yп пружины. Если при этом тело движется по вертикали вверх или вниз относительно направления ускорения свободного падения, значит векторная сумма сил F_т и F_уп дает равнодействующую, вызывающую ускорение тела, т. е.

F_т + F_уп=mа. (2.32)

Согласно приведенному выше определению понятия "вес", можно написать, что Р=-F_yп. Из (2.32) с учетом того, что F_т=mg, следует, что mg-mа=-F_yп. Следовательно, Р=m(g-а).

Невесомость и перегрузки.

Невесомость и перегрузка

Я рассказал ряд эпизодов, связанных с совершенствованием основных летных качеств боевого самолета. Но круг летных испытаний широк. Испытания на штопор — падение самолета с самовращением, испытания на прочность, невесомость занимают исключительно важное место в работе летчиков-испытателей.
В летные испытания все больше и больше проникает кинокамера. Возможности пытливого глаза кинообъектива трудно переоценить. Уникальный эксперимент, выполненный всего раз, в просмотровом зале становится повторимым.
Мы смотрим небольшой фильм, он еще не озвучен, его на днях отсняли. Интерес к нему необычайный: человек летает без крыльев! Да, крупным планом с экрана на вас двигается человек. Слегка подпрыгнув, он поднимает ноги и, коснувшись стены, шагает по ней, затем по потолку вниз головой, слегка размахивая свободными руками. Вдруг отделяется от потолка и летит по комнате, раскинув в стороны руки и ноги. Лицо спокойно; улыбаясь, он приглашает зрителей последовать его примеру.
Кинотрюк? Нет. Натурная съемка.
Объяснение всему — невесомость. С легкой руки космонавтов это слово стало довольно популярным. О том, что прикосновение к невесомости испытал каждый человек еще в детстве, никто как-то и не задумывался. Однако это так.
Качели — нехитрое устройство; они могут познакомить вас с ощущением невесомости. На старинной картине фламандской школы художник уловил и запечатлел состояние девушки, взлетающей вверх на качелях. Глаза в испуге расширены. От страха она судорожно вцепилась в канаты... Парень, согнув колени, раскачивает перекладину. Качели взметнулись высоко и здесь застыли на короткое мгновение... Вот она, невесомость! Короткий миг. Это самое острое ощущение, оно и отразилось в глазах девушки.
Но вернемся к фильму. Как он заснят?
Чтобы понять, обратимся к житейскому примеру: представим, что катимся с горы на санках; внизу, у подножья, устроен трамплин. Сани мчатся, развивая большую скорость, ветер бьет в лицо, слезятся глаза. Вот начинается трамплин. Сани взлетают на бугор, и в этот момент ощущаем, как сильно тебя прижимает к саням. Это действует перегрузка. Но вот трамплин, сани отрываются от земли... Наступает невесомость! Всего лишь на мгновение, и опять сани на снегу. Тут только бы удержаться!
Совершенно аналогичное происходит и в воздухе. По подобному профилю выполняется полет на создание искусственной невесомости. В воздухе самолет разгоняется, снижаясь. Крутизну разгона пилот может задать любую. Помогают двигатели, работающие на полном газу.
Когда скорость достигнута, начинается выполнение «трамплина». Пилот берет штурвал на себя, и самолет делает горку. В криволинейном полете действуют перегрузки; летчик и все присутствующие на борту ощущают сильное увеличение собственного веса [1], шея напрягается, чтобы удержать отяжелевшую голову.
Это ощущение тяжести длится недолго, пока самолет описывает дугу, выбираясь на подъем. Дальше самолет набирает высоту, и перегрузка исчезает. Но вдруг пассажиры судорожно хватаются за ремни, которыми они привязаны к креслам. Оказывается, летчик отдал штурвал от себя, и самолет в это время как бы пролетает в воздухе пространство за «трамплином». Тут весь экипаж, все предметы на борту подвергаются действию невесомости. Она может длиться в эксперименте секунд 35—40. А пассажиры, если они не привязаны, могут плавать по салону.
Вот в это время и снимался упомянутый фильм. Так впервые исследовалась работоспособность человека в условиях невесомости, что было чрезвычайно важно для подготовки космических полетов.
Летчикам, особенно пилотажникам, давно знакомо кратковременное состояние невесомости. Однако прежде на этом не сосредоточивали внимания. В авиации всегда больше занимались изучением перегрузок. Это и понятно — с ними приходится считаться, оглядываясь на прочность самолета.
Прочностные испытания многогранны. В их числе важнейшее — достижение максимальных эксплуатационных перегрузок в полете.

Билет №8

Импульс тела.

Основные законы механики — второй и третий законы Ньютона — заключают в себе возможность решения любой механической задачи. В следующих параграфах мы увидим, что применение законов Ньютона к решению задач часто можно облегчить, применяя следующий вывод из второго закона.

Подействуем на тело массы m постоянной силой f. Тогда ускорение тела также будет постоянно:

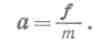(49.1)

Пусть в начальный момент промежутка времени t, в течение которого действовала сила, скорость тела была v₀, а в конечный момент этого промежутка скорость тела стала равна v. Напомним формулу (27.2), применимую для случая постоянного ускорения:

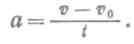
Из этой формулы и из формулы (49.1) следует:

mv—mv₀=ft. (49.2)

Произведение массы тела на его скорость называют импульсом (или количеством движения) тела. Импульс тела — векторная величина, так как скорость — вектор. Формула (49.2) выражает закон изменения импульса тела: изменение вектора импульса тела под действием постоянной силы равно произведению силы на время ее действия.

Если сила не остается постоянной, то формула (49.2) применима только для таких малых промежутков времени, за которые сила не успевает еще заметно измениться ни по величине, ни по направлению. При большом изменении силы формулой (49.2) также можно пользоваться, но в качестве / следует тогда брать среднее значение силы за рассматриваемый промежуток времени.

В случае прямолинейного движения тела формулу (49.2) можно написать в скалярном виде:

mv — mv₀ = ft. (49.3)

В этой формуле, как обычно, разные знаки величин v, v₀ и f будут обозначать противоположные направления скоростей и сил.

Импульс силы.

Покой и движение тела относительны, скорость движения тела зависит от выбора системы отсчета. По второму закону Ньютона независимо от того, находилось ли тело в покое или двигалось, изменение скорости его движения может происходить только при действии силы, т.е. в результате взаимодействия с другими телами.

Если на тело массой m в течение времени t действует сила F и скорость его движения изменяется от V₀ до V, то ускорение a движения тела равно

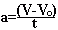
На основании второго закона Ньютона для силы F можно написать выражение

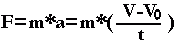
Из этого равенства следует, что

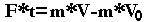
Из доказанного равенства можно сделать вывод, что физическая величина, равная произведению силы F на время t ее действия, называется импульсом силы.

Закон сохранения импульса.

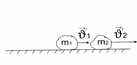
До взаимодействия

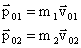
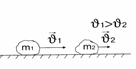
После взаимодействия

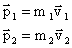
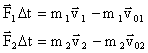
Согласно 3 з-ну Ньютона: 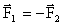, следовательно:

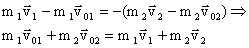
Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной.

Замкнутой называется система тел, взаимодействующих только друг с другом и не взаимодействующих с другими телами. Можно пользоваться и для незамкнутых систем, если сумма внешних сил, действующих на тела системы, равна нулю, или процесс происходит очень быстро, когда внешними воздействиями можно пренебречь (взрыв, атомные процессы).

В общем виде: т.к. система замкнутая, то 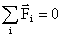, следовательно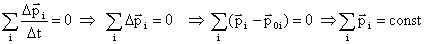

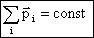
Билет №9

Работа и мощность.

При перемещении тела под действием силы совершается работа. Следовательно, работу А можно выразить произведением силы Р на путь S, т. е.

A = PS кГ*м. (25)

Работа, совершенная в единицу времени, называется мощностью и выражается формулой

N = A/t = (PS)/t = (pv)/60 [кГм/сек],(26)

где Р — сила, кГ;

v — скорость, м/мин.

Единицей измерения мощности является ватт (вт). Для выражения мощности в киловаттах применяют формулу N =A/(60*102) квт.

Часть мощности N _эф двигателя станка затрачивается на полезную работу, другая часть N_тр — на преодоление сил трения. Общая затрачиваемая мощность N=N_эф + N_тр.

Полезная работа является частью затраченной работы, а отношение полезной работы к затраченной называется коэффициентом полезного действия (к. п. д.) станка и обозначается буквойη(эта): η = (N_эф / N)* 100%. (27)

Чем меньше трение, тем большая часть мощности будет использована на полезную работу и, следовательно, выше к. п. д. станка.

Коэффициенты полезного действия работы некоторых систем и устройств составляют: ременной передачи с плоскими ремнями и натяжным роликом — 0,98, цепной передачи при хорошей смазке— 0,97, подшипников скольжения одного вала — 0,98, подшипников качения одного вала —0,99, пары зубчатых колес при хорошей смазке —0,99—0,993, червячной пары в зависимости от скорости вращения и смазки — от 0,3 до 0,97.

Механическая энергия.

Механическая энергия

Механическое состояние тела (системы тел) определяется его положением относительно других тел (координатами) и его скоростью.

Если изменяется хотя бы одна из этих величин, то говорят об изменении механического состояния тела.

Состояние данной системы тел обязательно изменяется, если внешние силы совершают отличную от нуля работу.

Количественно механическое состояние системы и его изменение характеризуется механической энергией W.

Механическая энергия — это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу. Изменение механической энергии ΔW равно работе приложенных к системе внешних сил:

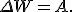
Значение энергии системы в данном состоянии не зависит от пути перехода ее в это состояние.

Закон сохранения энергии.

Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.

С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.

В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Говорят, что возможен переход энергии одного типа в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Ввиду условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.

Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первого начала термодинамики, а в электродинамике — теорема Пойнтинга.

С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.

Билет №10

1. Механические колебания – это повторяющееся движение, при котором тело многократно проходит одно и то же положение в пространстве.   Различают периодические и непериодические колебания. Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени. Примерами механических колебаний могут служить движение шара на пружине, на нити, движение ножек звучащего камертона или молекул воздуха вблизи него. В физике рассматривают и другие колебания – процессы, обладающие той или иной степенью повторяемости во времени, например, электромагнитные колебания. 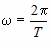Колебания можно классифицировать по условиям возникновения свободные, вынужденные, автоколебания и по характеру изменения во времени кинематических характеристик (пилообразные, гармонические, затухающие) 2. Колебательное движение это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени. Учение о колебательном движении в физике выделяют особо. Это обусловлено общностью закономерностей колебательного движения различной природы и методов его исследования. Механические, акустические, электромагнитные колебания и волны рассматриваются с единой точки зрения. Колебательное движение свойственно всем явлениям природы. Внутри любого живого организма непрерывно происходят ритмично повторяющиеся процессы, например биение сердца.

3. Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равени не зависит^[1] от амплитуды и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.

Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида

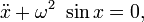
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 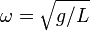где L ― длина подвеса, g ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид: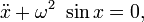

Билет№11

1. Колебательные движения, или просто колебания, широко распространены в природе. Заставить предмет колебаться, т. е. совершать повторяющиеся движения, очень просто.

Механические колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.

Повторяются движения поршней в двигателе автомобиля, поплавка на волне, ветки дерева на ветру, нашего сердца. Все это различные примеры колебаний.

Свободные колебания. Группу тел, движение которых мы изучаем, называют в механике системой тел или просто системой. Напомним, что силы, действующие между толами системы, называют внутренними. Внешними си-чами называют силы, действующие на тела системы со стороны тел, не входящих в нее.

Самым простым видом колебаний являются свободные колебания. Свободными колебаниями называются колебания в системе под действием внутренних сил, после того как система выведена из положения равновесия и предоставлена затем самой себе.

Колебания груза, прикрепленного к пружине, или груза, подвешенного на нити, — это примеры свободных колебаний. После выведения системы из положения равновесия создаются условия, при которых груз колеблется без воздействия внешних сил.Однако с течением времени колебания затухают, так как на тела системы всегда действуют силы сопротивления. Под действием внутренних сил и сил сопротивления система совершает затухающие колебания.

Вынужденные колебания. Для того чтобы колебания не затухали, на тела системы должна действовать периодически изменяющаяся сила. Постоянная сила не может поддерживать колебания, так как под действием этой силы может измениться только положение равновесия, относительно которого происходят колебания.

Вынужденными колебаниями называются колебания тел под действием внешних периодически изменяющихся сил.

Колебания бывают свободными, затухающими и вынужденными. Наибольшее значение имеют вынужденные колебания. Ф.упр. ф.т

2. Уравнение гармонических колебаний можно записать в виде:
x = A*sin(wt + f₀), где

x - смещение точки от положения равновесия,
A - амплитуда колебаний,
(wt+f₀) - фаза колебаний,
f₀ - начальная фаза,
w - частота,
t - время.

гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.

3.Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.
Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.
Для пределения условий возникновения режима резонанса в электрической цепи нужно:
· найти ее комплексное сопротивление или проводимость;
· выделить мнимую часть и приравнять нулю.
Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.
Уравнение Im[Z]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.
В электрических цепях резонанс может рассматриваться в задачах:
· анализа этого явления при вариации параметров цепи;
· синтеза цепи с заданными резонансными параметрами.
Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.

Билет№12

1. Скорость распространения волн:

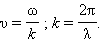Скорость распространения поперечных волн в струне:

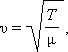T – натяжение; μ – погонная масса.

Скорость распространения продольных волн в упругом стержне

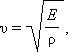E – модуль Юнга; ρ –плотность.

Скорость распространения продольных волн в безграничных средах:

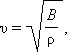B – модуль все стороннего сжатия; ρ – плотность.

Скорость звука в газе:

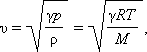T – абсолютная температура; R- универсальная