Равновесия в водных растворах кислот и оснований
Согласно протолитической теории к кислотам относятся химические соединения, способные в растворах отдавать протоны, а к основаниям — вещества, способные присоединять протоны. Для того чтобы кислота могла отдать протон, необходимо присутствие основания, принимающего этот протон. Отдавая протон, кислота образует сопряженное с ней основание, а основание, принимая протон, образует сопряженную с ним кислоту.
В водных растворах кислот имеет место следующее равновесие:
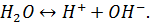 (1.1)
(1.1)
Константа4 равновесия этой реакции
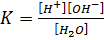 (1.2)
(1.2)
Выражение для константы равновесия запишется следующим образом:
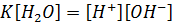 (1.3)
(1.3)
Ионное произведение является величиной постоянной при постоянной температуре. Эту константу называют ионным произведением воды, которое равно
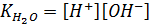 (1.4)
(1.4)
В чистой воде [Н+] = [ОН-]. При избытке [ОН-]
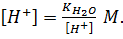 (1.5)
(1.5)
При избытке [Н+]
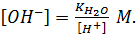 (1.6)
(1.6)
Концентрацию водородных ионов обычно используют для характеристики среды. В большинстве расчетов, относящихся к кислотно-основному равновесию, концентрации (и другие величины) удобно выражать в виде отрицательных логарифмов этих величин, обозначаемых знаком „р". Тогда
-lg[H+] = pH; (1.7)
-lg[OH-] = pOH. (1.8)
Ионное произведение воды тоже можно выразить в логарифмическом виде
рН + рОН = р 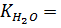 14. (1.9)
14. (1.9)
Пример 1. Вычислить рН раствора, концентрация водородных ионов в котором равна 0,02 М. Решение.
рН = - lg [Н+] = - Ig 2  10-2 = 2-0,30 = 1,70.
10-2 = 2-0,30 = 1,70.
Решая обратную задачу, по известному значению рН легко найти концентрации водородных и гидроксид-ионов.
Пример 2. Вычислить [H+ ] и [ОН-] раствора, рН которого равен 10,33.
Решение.
[Н+] = 1  10-10,33 =1
10-10,33 =1  100,67
100,67  10-11 = 4,7
10-11 = 4,7  10-11 М.
10-11 М.
рОН = 14 -10,33=3,67.
[ОН-] = 1  10-3,67 =1
10-3,67 =1  100,33
100,33  10-4 =2,1
10-4 =2,1  10-4 М.
10-4 М.
Сильные кислоты (НХ) и сильные основание (МОН) в водных растворах практически полностью диссоциированы
НХ = Н+ + Х-; (1.10)
МОН=М+ + ОН-. (1.11)
Концентрации Н+ и ОН- в этих растворах в первом приближении можно считать равными общей концентрации СА кислоты (НХ) и соответственно основания (МОН). Следовательно,
рH = -lgCHX; (1.12)
pOH = -lgCMOH. (1.13)
Эти выражения являются приближенными. В более строгих расчетах концентрацию электролитов следует заменять активностью ионов
Пример 3. Вычислить рН 0,0018%-ного раствора хлороводородной кислоты.
Решение. Найдем концентрацию НСl, выраженную в М, учитывая, что молекулярная масса НCl 36,46:
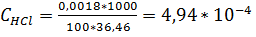 М;
М;
рН = - lg4,94 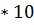 -4 =-lg4,94 - lg 10-4 = 4-0,69 = 3,31.
-4 =-lg4,94 - lg 10-4 = 4-0,69 = 3,31.
Пример 5. К 3 л воды прибавлен 1 г HN03 (ρ=1,4). Вычислить рН раствора.
Решение. По таблицам находим, что в 100 г азотной кислоты (ρ = 1,4) содержится 65,3 г HN03. Тогда концентрация HN03 в М будет равна
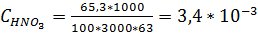 M,
M,
рН = - lg3,4  10-3 = 3 - lg3,4 = 2,47.
10-3 = 3 - lg3,4 = 2,47.
B случае слабых кислот константа равновесия реакции (1.1) может быть выражена следующим уравнением:
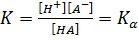 (1.14)
(1.14)
где 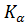 — константа диссоциации кислоты НА.
— константа диссоциации кислоты НА.
Если общую концентрацию кислоты обозначить СНА, а равновесную [НА], то
[HA]=CHA-[H+]. (1.15)
Из уравнения (1.1) следует, что [Н+] = [А-]. Тогда выражение константы диссоциации слабой кислоты можно записать следующим образом:
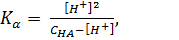 (1.16)
(1.16)
отсюда легко найти концентрацию [Н+]
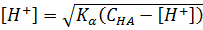 (1.17)
(1.17)
Если кислота диссоциирована в незначительной . степени (102[H+] ≤СНА), то приближенно можно считать, что
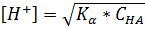 ; (1.18)
; (1.18)
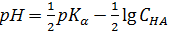 . (1.19)
. (1.19)
Слабое основание, как и слабая кислота, в водных растворах диссоциирует неполностью
ВОН 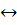 В+ + ОН-, (1.20)
В+ + ОН-, (1.20)
как и для слабой кислоты,
[ВОН] = СВОН - [ОН-]. (1.21)
Поскольку [В+] = [ОН-], уравнение для константы диссоциации слабого основания будет иметь вид
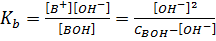 (1.22)
(1.22)
и
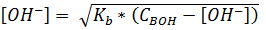 (1.23)
(1.23)
Когда [ОН-] 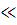 СВОН(102[ОН-]≤СВОН), можно принять
СВОН(102[ОН-]≤СВОН), можно принять
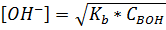 ; (1.24)
; (1.24)
и
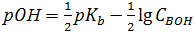 ; (1.25)
; (1.25)
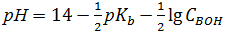 . (1.26)
. (1.26)
Пример 6. Вычислить рН 0,017 М раствора муравьиной кислоты.
Решение.
НСООН 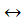 Н+ + НСОО-,
Н+ + НСОО-,
Снсоон = 0,017 = 1,7  10-2 M,
10-2 M,
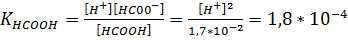 ,
,
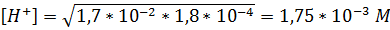 ,
,
рН = - lg 1,75  10-3 = 3 - lg 1,75 = 2,76.
10-3 = 3 - lg 1,75 = 2,76.
Пример 7. Вычислить рН 0,06 М раствора аммиака.
Решение.
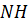 3 +
3 + 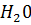 =
= 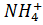 + ОН-,
+ ОН-,
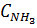 = 0,06 =
= 0,06 = 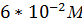 ,
,
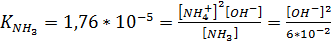 ,
,
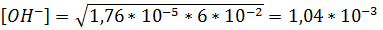 M,
M,
pOH = 3 - lg 1,04 = 2,98,
рН = 14 - 2,98 = 11,02.
Диссоциация слабых электролитов количественно характеризуется также степенью электролитической диссоциации (α). Степень диссоциации представляет собой отношение концентрации вещества, распавшегося на ионы, к общей его концентрации в растворе. Между константой диссоциации электролита Кα и α существует следующая зависимость:
КА = 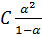 , (1.27)
, (1.27)
где С — молярная концентрация слабого электролита. Если α мала (α<5%), применимо приближенное уравнение 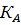 =
= 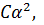 откуда
откуда
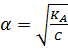 (1.28)
(1.28)
Пример 8. Вычислить степень диссоциации муравьиной кислоты в 1,5%-ном растворе.
Решение. Находим молярную концентрацию НСООН (М. м. = 46)
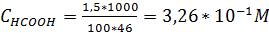 .
.
Формиат-ион и ион водорода образуются только в результате диссоциации муравьиной кислоты, следовательно, их концентрации равны
[Н+] = [НСОО-]=xМ;
[НСООН] = (3,26 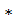 10-1 - х) М, отсюда
10-1 - х) М, отсюда
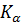 = 1,8
= 1,8 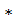 10-1 =
10-1 = 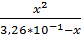 .
.
Если концентрация диссоциированной части мала по сравнению с общей концентрацией кислоты, то в знаменателе ею, как алгебраическим слагаемым, можно пренебречь. Тогда
х = [Н+] = [НСОО-] = 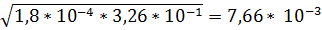 М,
М,
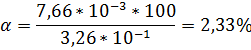
Пример 9. При какой концентрации бензойная кислота диссоциирована на 10%?
Решение. Если неизвестную общую концентрацию обозначить 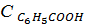 ,то концентрация каждого из ионов будет равна
,то концентрация каждого из ионов будет равна
[Н+] = [С6Н5СОО-] = 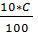 = 1
= 1 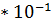 CM,
CM,
а концентрация недиссоциированной части будет составлять
[С6Н5СООН] = С - 1  10-1 = 9
10-1 = 9  10-1 СМ,
10-1 СМ,
отсюда
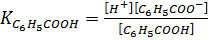 ,
,
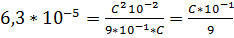 ,
,
или
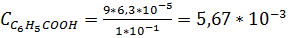 М.
М.
Пример 10. Уксусная кислота в 3%-ном растворе диссоциирована на 0,59%. Вычислить приближенное значение константы диссоциации.
Решение. Находим молярную концентрацию СН3СООН(М. м. = 60,05).
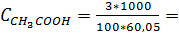 0,4996 М;
0,4996 М;
СН3СООН 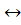 Н+ + СН3СОО-,
Н+ + СН3СОО-,
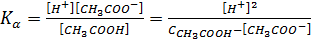 ,
,
[Н+] = [СНзСОО-] = 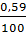
 0,4996 = 0,00295 М.
0,4996 = 0,00295 М.
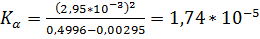 .
.
Задачи
