Реологические и фильтрационные свойства неньютоновских нефтей

Ньютоновские жидкости

Эффективность процессов разработки нефтяных месторождений в значительной степени определяется особенностями фильтрации пластовых жидкостей в пористой среде. Пластовая вода, содержащая растворенные соли, а также закачиваемая через нагнетательные скважины пресная вода является молекулярными растворами и относятся к истинным жидкостям.

Течение истинных жидкостей подчиняется закону вязкого течения Нью­тона (1642-1726 гг.). Для осмысливания этого закона представим тонкий слой вязкой жидкости между двумя параллельными пластинками, площадь каждой из которых S и расстояние между которыми h (рис. 2.1). Одна пластинка непод­вижна, а к другой приложено сдвигающее усилие F. В установившемся движе­нии усилие должно уравновешиваться со стороны жидкости силой, обусловлен­ной вязкостью, а подвижная пластинка должна перемещаться равномерно со скоростью и.

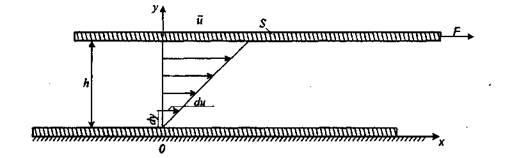
Рис. 2.1. Схема движения вязкой жидкости между подвижной и неподвижной пластинками

В этом случае уравнение вязкого течения Ньютона (1687 г.) записывается в следующем виде:

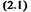
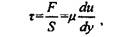
где х - напряжение сдвига, поддерживающее течение жидкости, Н/м², т.е. касательное усилие на единицу площади, приложенное к слоям жидкости, от­стоящим друг от друга на расстоянии dy при разности скоростей между ними du;

du/dy - градиент скорости (изменение скорости в направлении, перпендику­лярном течению), с"';

ц - коэффициент пропорциональности, носящий название динамической вязкости, Па-с.

Вязкость истинных растворов зависит от природы жидкости, температуры и давления.

Жидкости, течение которых подчиняется закону вязкого течения Ньютона, названы ньютоновскими.

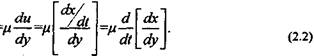
Но dx/ify представляет собой сдвиг слоев у (деформацию). Отсюда следует выражение для градиента скорости сдвига:

Формуле (2.1) можно придать другой вид (см. рис. 2.1):

то есть у ньютоновских жидкостей скорость сдвига у пропорциональна касательному напряжению сдвига г и обратно пропорциональна динамической вязкости /л. Зависимость между г и у, очевидно, является прямой линией, про­ходящей через начало координат.

Таким образом, истинные или молекулярные растворы являются ньютонов­скими жидкостями. Примерами таких жидкостей, кроме воды, могут служить жидкие индивидуальные углеводороды с числом атомов углерода до 17 (спирт, бензол и т.д.).

Следует заметить, что закон Ньютона справедлив лишь при установившем­ся ламинарном течении истинной жидкости.

Вязкость жидкости определяется более точно, если имеется график зави­симости между напряжением сдвига т и градиентом скорости dx/dy - линия консистентности. Линия консистентности ньютоновской жидкости представ­ляет собой прямую линию, исходящую из начала координат (рис. 2.2). Это ука­зывает на то, что истинные жидкости текут при сколь угодно малых напряжени­ях сдвига.

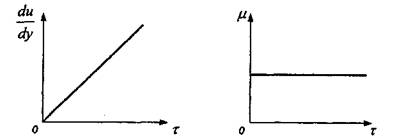
Рис. 2.2. Линия консистентности и зависимость динамической вязкости fj от напряжения сдвига г для ньютоновских жидкостей

Параметры, с помощью которых можно описывать течение веществ, назы­ваются реологическими параметрами.

Таким образом, единственным реологическим параметром, характеризую­щим течение ньютоновской жидкости, является динамическая вязкость.

В смешанной системе единиц напряжение сдвига г измеряется в дин/см² (1 дин/см²=0,1 Н/м²). Единица измерения динамической вязкости в честь фран­цузского ученого Пуазейля, впервые изучившего движение жидкостей в капил­лярах, названа Пуазом (1сП=1мПас).

Неньютоновские жидкости

Течение некоторых жидкостей (коллоидных растворов, нефтей с большим содержанием асфальтенов и парафинов, растворы полимеров и т.д.) не подчи­няются закону Ньютона. Такие жидкости в реологии принято называть ненью­тоновскимиили аномальными.

Закон Ньютона обычно нарушается при течении коллоидных растворов с удлиненными частицами дисперсной фазы, способными деформироваться в поле напряжений и структурированных систем. Такие коллоидные системы обладают определенными механическими свойствами - пластичностью, упругостью, прочностью и вязкостью. Эти свойства в большинстве случаев связаны с обра­зованием структуры в жидкости, и поэтому их часто называют структурно -механическими или реологическими свойствами.

Основы реологии коллоидных растворов впервые изучены Ф.Н.Шведовым, Бингамом и Грином. В 1889 году Ф.Н. Шведов, позже в 1916 году Бингам уста­новили, что течение системы с пространственной структурой начинается лишь тогда, когда напряжение сдвига т превышает определенное критическое значе­ние х₀ (рис. 2.3), необходимое для разрушения в жидкости структурной сетки. Такое течение было названо пластическим, а критическое напряжение сдвига -пределом текучести или предельным напряжением сдвига.

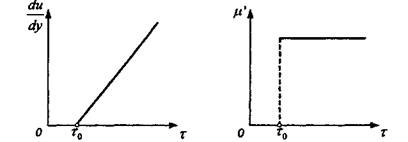
Рис. 2.3. Линия консистентности и зависимость пластической вязкости ju' от напряжения сдвига гдля пластических жидкостей

где ц ' - пластическая вязкость системы.

Систему, течение которой подчиняется такой идеализированной схеме, в реологии называют телом Бингама или бингановскими пластиками. Они опи­сываются следующим реологическим уравнением Бингама - Шведова:

Вязкость истинных растворов зависит от природы жидкости, температуры и давления.

Жидкости, течение которых подчиняется закону вязкого течения Ньютона, названы ньютоновскими.

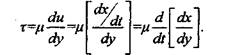
Но dx/dy представляет собой сдвиг слоев у (деформацию). Отсюда следует выражение для градиента скорости сдвига:

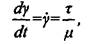
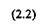
Формуле (2.1) можно придать другой вид (см. рис. 2.1):

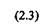то есть у ньютоновских жидкостей скорость сдвига у пропорциональна касательному напряжению сдвига г и обратно пропорциональна динамической вязкости fi. Зависимость между г и у, очевидно, является прямой линией, про­ходящей через начало координат.

Таким образом, истинные или молекулярные растворы являются ньютонов­скими жидкостями. Примерами таких жидкостей, кроме воды, могут служить жидкие индивидуальные углеводороды с числом атомов углерода до 17 (спирт, бензол и т.д.).

Следует заметить, что закон Ньютона справедлив лишь при установившем­ся ламинарном течении истинной жидкости.

Вязкость жидкости определяется более точно, если имеется график зави­симости между напряжением сдвига т и градиентом скорости dx/dy - линия консистентное/пи. Линия консистентности ньютоновской жидкости представ­ляет собой прямую линию, исходящую из начала координат (рис. 2.2). Это ука­зывает на то, что истинные жидкости текут при сколь угодно малых напряжени­ях сдвига.

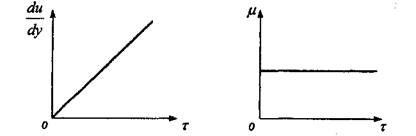
Рис. 2.2. Линия консистентности и зависимость динамической вязкости // от напряжения сдвига г для ньютоновских жидкостей

Параметры, с помощью которых можно описывать течение веществ, назы­ваются реологическими параметрами.

Таким образом, единственным реологическим параметром, характеризую­щим течение ньютоновской жидкости, является динамическая вязкость.

В смешанной системе единиц напряжение сдвига т измеряется в дин/см² (1 дин/см²=0,1 Н/м²). Единица измерения динамической вязкости в честь фран­цузского ученого Пуазейля, впервые изучившего движение жидкостей в капил­лярах, названа Пуазом (1сП=1мПас).

2.2. Неньютоновские жидкости

Течение некоторых жидкостей (коллоидных растворов, нефтей с большим содержанием асфальтенов и парафинов, растворы полимеров и т.д.) не подчи­няются закону Ньютона. Такие жидкости в реологии принято называть ненью­тоновскимиили аномальными.

Закон Ньютона обычно нарушается при течении коллоидных растворов с удлиненными частицами дисперсной фазы, способными деформироваться в поле напряжений и структурированных систем. Такие коллоидные системы обладают определенными механическими свойствами - пластичностью, упругостью, прочностью и вязкостью. Эти свойства в большинстве случаев связаны с обра­зованием структуры в жидкости, и поэтому их часто называют структурно -механическими или реологическими свойствами.

Основы реологии коллоидных растворов впервые изучены Ф.Н.Шведовым, Бингамом и Грином. В 1889 году Ф.Н. Шведов, позже в 1916 году Бингам уста­новили, что течение системы с пространственной структурой начинается лишь тогда, когда напряжение сдвига х превышает определенное критическое значе­ние т₀ (рис. 2.3), необходимое для разрушения в жидкости структурной сетки. Такое течение было названо пластическим, а критическое напряжение сдвига -пределом текучести или предельным напряжением сдвига.

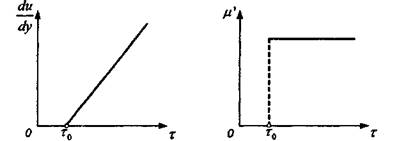
Рис. 2.3. Линия консистентности и зависимость пластической вязкости fx от напряжения сдвига г для пластических жидкостей

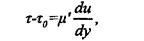
где /л ' - пластическая вязкость системы.

Систему, течение которой подчиняется такой идеализированной схеме, в реологии называют телом Бингама или бингановскими пластиками. Они опи­сываются следующим реологическим уравнением Бингама - Шведова:

Линия консистентности бингамова тела выражается прямой линией, отсе­кающей отрезок на оси абсцисс, равный т₀ от начала координат (рис. 2.3).

Для ньютоновских жидкостей предельное напряжение сдвига равно нулю, и уравнение (2.4) переходит в закон Ньютона, а пластическая вязкость - и истин­ную вязкость. Из уравнения (2.4) следует: система до т₀ упруго деформируется, после этого течет с постоянной пластической вязкостью

В области упругой деформации вязкость бингамовского пластика чрезвы­чайно высокая. Здесь упруго деформируется структурный "каркас" из частиц дисперсной фазы. При превышении т₀, согласно уравнению Бингама - Шведова, структурная сетка мгновенно разрушается и вязкость системы принимает посто­янное значение.

Примером систем, хорошо подчиняющихся уравнению (2.4), могут служить нефти с высоким содержанием парафинов при температурах ниже температуры кристаллизации.

Однако у многих реальных структурированных коллоидных систем линия консистентности оказывается не прямой, а кривой, отсекающей на оси напряже­ний сдвига некоторый отрезок (рис. 2.4). В этом случае при достижении предела текучести структура разрушается не сразу, а постепенно, по мере увеличения скорости сдвига - упругопластические жидкости.

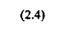
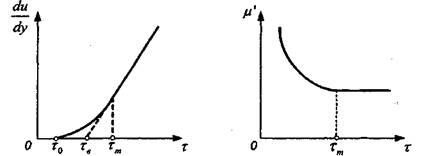
Рис. 2.4. Линия консистентности и зависимость кажущейся вязкости ju' от напряжения сдвига т щ\я упругопластических жидкостей

Для характеристики механических свойств структуры в этом случае вводят три параметра: минимальный предел текучести (статическое напряжение сдвига), соответствующий началу течения жидкости х₀\ предел текучести по Бингаму (динамическое напряжение сдвига по Бингаму) т_а\ максимальный предел текучести (напряжение сдвига предельного разрушения структуры), при котором кривая переходит в прямую линию т_т (рис. 2.4). Значение т_т равно напряжению, при котором структура в жидкости полностью разрушается.

Математическая модель упругопластической жидкости выражается сле­дующей степенной зависимостью:

где к - мера консистентности жидкости (с увеличением вязкости жидкости мера консистентности растет); п - степень неньютоновского поведения системы. Значение п всегда меньше единицы. Чем больше п отличается от единицы, тем сильнее проявляются неньютоновские свойства жидкости.

Кажущаяся вязкость системы определяется из соотношения

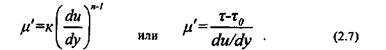В качестве примера упругопластической жидкости можно указать на мас­ляную краску, буровые растворы, высокопарафинистую дегазированную нефть с температурой ниже температуры насыщения парафином. Например, линии кон­систентности такой формы (рис. 2.4) обнаружены у некоторых нефтей месторо­ждений Азербайджана, Узбекистана и Казахстана.

На практике наличие статического напряжения сдвига у жидкости часто иг­рает положительную роль. Так, толщина слоя краски, оставшейся после нанесе­ния на вертикальную поверхность определяется величиной т₀. Следовательно, изменяя значение т₀, можно регулировать расход краски на покраску.

При бурении скважин процесс проходки часто прерывается. Применение качественных буровых растворов позволяет удерживать во взвешенном состоя­нии часть шлама выбуренной породы и тем самым предотвращать прихват буро­вого инструмента. При этом регулирование количества и размеров частиц удер­живаемого в буровом растворе шлама достигается подбором параметра т₀.

То же самое наблюдается и при течении растворов высокомолекулярных соединений с гибкими, свернутыми в клубок макромолекулами, например у водных растворов полимеров. Здесь снижение вязкости обусловлено распрямле­нием молекул и ориентацией в направлении потока. Система ведет себя при те­чении как жидкость, в которой взвешены частицы, способные ориентироваться или деформироваться.

Во всех этих случаях речь идет о кажущейся или эффективной вязкости, так как истинная вязкость жидкости от скорости течения не зависит.

Механические свойства псевдопластической (вязкопластической) жид­кости характеризуются двумя параметрами: динамическим напряжением сдви­га по Бингаму т_в и напряжением сдвига предельного разрушения структуры или ориентирования частиц в потоке т_т (рис. 2.5).

Реологическое уравнение у таких систем выражают в виде степенной зави­симости

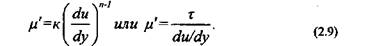
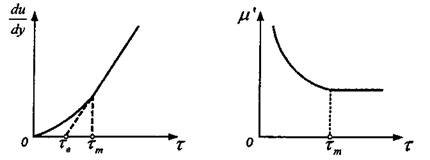
Рис. 2.5. Линия консистентное™ и зависимость кажущейся вязкости р.' от напряжения сдвига г для вязкопластических жидкостей

Кажущаяся вязкость вязкопластической жидкости выражается следующим образом:

Здесь и в предыдущем случае необходимо иметь в виду, что для реальной жидкости п является переменным и зависящим от скорости сдвига. Поэтому при решении практических задач значение п следует определять в ограниченном пределе скоростей сдвига. Кроме того, неудобство использования степенного закона обусловлено зависимостью размерности меры консистентности от пока­зателя степени.

В настоящее время для увеличения нефтеотдачи пластов, при воздействии на призабойную зону скважин и проведении изоляционных работ применяются растворы полимеров. В некоторых условиях в пористой среде они проявляют свойства дилатантных жидкостей. Термин "дилатанткая" можно применять для тех жидкостей, кажущаяся вязкость которых с увеличением скорости сдвига повышается (рис. 2.6).

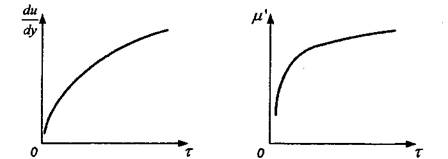
Рис. 2.6. Линия консистентности и зависимость кажущейся вязкости

m' от напряжения сдвига г для дилатантных жидкостей

Такой тип течения был впервые обнаружен Рейнольдсом в суспензиях при большом содержании твердой фазы и крахмальных клейстерах. Рейнольде при объяснении дилатантных свойств суспензии высказывает предположение о том, что в состоянии покоя твердые частицы имеют наиболее плотную упаковку, а пространство между частицами заполнено жидкостью. При течении суспензии с небольшой скоростью жидкость служит смазкой, уменьшающей трение между частицами, и напряжения сдвига невелики. При больших скоростях сдвига плот­ная упаковка частиц нарушается, увеличивается объем суспензии и уже при но­вой структуре жидкости ее недостаточно для смазки трущихся друг о друга час­тиц. Действующие напряжения сдвига при этом увеличивается значительно бы­стрее, чем скорости сдвига.

Для описания реологического поведения дилатантной жидкости также при­меняют степенной закон, но с показателем степени больше единицы.

23. Аномалии вязкости нефти

Исследованиями установлено, что асфальтеносодержащие пластовые и де­газированные нефти при температурах выше температуры насыщения парафи­ном являются аномально вязкими. Линии консистентности этих нефтей по форме аналогичны полным реологическим кривым С. Оствальда (рис. 2.7).

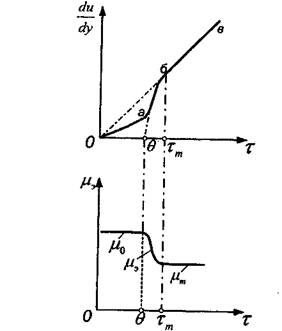
Рис. 2.7. Линия консистентности и зависимость эффективной вязкости m^’ ,

от напряжения сдвига для аномально вязких нефтей

По классификации акад. П.А. Ребиндера кривые консистентности такой формы характерны для жидкообразных структурированных коллоидных систем. Структурная сетка образована в них мицеллами асфальтенов и относится к типу коагуляционных структур. Как правило, начальная температура в пласте выше температуры насыщения нефти парафином, поэтому асфальтеносодержащие нефти следует считать аномально вязкими.

Рассмотрим более подробно форму линии течения таких нефтей и сущность процессов, происходящих на каждом характерном участке кривой консистент­ности. На кривой консистентности (рис. 2.7) можно выделить два линейных уча­стка, различающихся углом наклона к оси напряжения сдвига.

Участок (0-а) находится в начале кривой консистентности - в области ма­лых напряжений и скоростей сдвига. Угол наклона кривой на этом участке не­большой, течение нефти в этой области происходит практически без разрушения структуры, поэтому ее вязкость наибольшая. Продолжение участка (0-а) прохо­дит через начало координат.

По П.А. Ребиндеру в этой области разрушение структуры сопровождается полным тиксотропным ее восстановлением, и система движется с практически не разрушенной структурой, т.е. наблюдается явление ползучести. Вязкость нефти постоянна и названа наибольшей предельной вязкостью практически не разрушенной структуры д>.

Конечный участок линии консистентности (б-в) расположен правее напряжения сдвига предельного разрушения структуры (НСПРС) т_т до об­ласти турбулентного течения. Продолжение реологической линии этого участка проходит через начало координат. Вязкость нефти в этой области постоянная и наименьшая. Она названа наименьшей вязкостью предельно разрушенной структуры /^.

При выполнении практических расчетов можно принять, что при превыше­нии предельного динамического напряжения сдвига (ПДНС) в эффективная вязкость /4 начинает уменьшаться и при действующих напряжениях сдвига, превышающих т_т, достигает наименьшей величины д>- В этой области (а~б) эф­фективная или структурная вязкость соответствует равновесному состоянию процессов разрушения и восстановления структуры, протекающих одновремен­но в установившемся ламинарном потоке. От точки "а" до точки перегиба кри­вой (а-б) превалирует процесс восстановления структуры, а в дальнейшем от то­чки перегиба до "б" - процесс разрушения пространственной структурной сетки.

Из изложенного следует, что вязкость нефти зависит от напряжений и ско­ростей сдвига. Такая зависимость в реологии названа аномалией вязкости. В частности, у неньютоновских жидкостей, кроме дилатантных, кажущаяся или эффективная вязкость уменьшается с ростом действующих напряжений сдвига т.

Для аномально вязких нефтей связь между эффективной вязкостью и на­пряжением сдвига выражается следующей формулой:

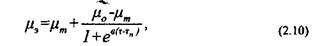
где Т„ - некоторое напряжение сдвига, соответствующее началу сильного разрушения структуры. Оно находится из экспериментальной зависимости

М_э ~ J\4 по величине М_э ⁼ t*_m ⁺ ° '_ ^m , т.е. по величине эффективной вяз­кости, соответствующей условию Т = Т„;

Ь - коэффициент, характеризующий скорость разрушения структуры в системе. Для нахождения этого коэффициента используется любая точка экспе­риментальной кривой /и, = Дт), лежащей в диапазоне напряжений сдвига от т„ до т_т. Коэффициент Ъ находится из формулы (2.10) по значениям х и jx, в этой экспериментальной точке и найденной ранее величине т_п.

К аномально вязким системам следует отнести фильтрующиеся без переры­ва нефти с температурой, превышающей температуру насыщения парафином. После появления в объеме нефти кристалликов парафина до температуры, близ­кой к температуре массовой кристаллизации, аномалии вязкости значительно усиливаются. При этом у нефтей с содержанием парафинов до 6% масс, при не­прерывном движении наблюдается линия типа С. Оствальда. Эти выводы осно­ваны на результатах многолетних исследований пластовых нефтей месторожде­ний Башкирии, Татарии, Западного Казахстана и Коми.

Нефть, содержащая асфальтены и парафины, относится к тиксотропным системам. Такие системы способны к изотермическому восстановлению струк­туры, разрушенной при механическом воздействии. В процессе теплового дви­жения частицы дисперсной фазы принимают такое взаимное расположение, при котором система обладает минимумом энергии и становится термодинамически более устойчивой. В частности, в состоянии покоя структура упрочняется на­столько, что при возобновлении течения вязкости при тех же скоростях сдвига будет выше, чем до перерыва в движении.

Тиксотропные свойства нефти ведут к усилению структурно- механических свойств. Например, с увеличением продолжительности покоя предельное дина­мическое напряжение сдвига (ПДНС) растет. Зависимость этого параметра от времени покоя записывается в виде

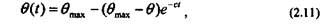
где в - ПДНС нефти в условиях непрерывного движения; #_тах - максималь­ное значение ПДНС нефти, находившейся в покое более 35 часов; t- время по­коя; с =0,42 - коэффициент, зависящий от свойств нефти.

Следует учесть, что наиболее быстро ПДНС увеличивается в течение 10 ча­сов после прекращения движения. В дальнейшем прочность структуры увеличи­вается незначительно. Рост ПДНС прекращается после 35 часов покоя нефти. Зависимость между <9_тах и 0 приближенно оценивается формулой

Тиксотропные свойства являются одной из причин проявления сверхано­малий вязкости нефтей. Хотя линия консистентности по-прежнему исходит из начала координат, но в этом случае появляется многозначность вязкости. В определенных пределах каждому напряжению сдвига соответствует от двух до трех значений коэффициента вязкости (рис. 2.8).

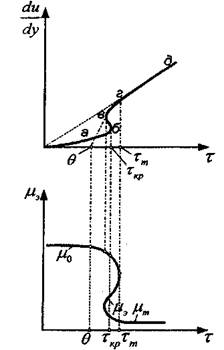Рис. 2.8. Линия консистентности и зависимость эффективной вязкости р, от напряжения сдвига х для сверханомально вязких нефтей

Рассмотрим более подробно форму линии течения таких нефтей и сущность процессов, происходящих на каждом характерном участке кривой консистент­ности.

участок (0-а), где напряжение сдвига прямо пропорционально скорости сдвига, т.е. нижняя ньютоновская область течения с вязкостью практически не разрушенной структуры. Участок расположен левее предельного динамического напряжения сдвига.

участок (а-б-в) соответствует интенсивному разрушению структуры и резкому снижению сопротивления течению - режим проявления сверханомалии. На этом участке напряжение сдвига сначала (а-б) увеличивается, а затем (бив) уменьшается с ростом градиента скорости. Здесь наблюдаются сильные анома­лии вязкости. Наибольшее значение напряжения сдвига на этом участке, соот­ветствующее точке "б", названо критическим напряжением сдвига.

практически вертикальный участок (в-г) соответствует переходу от сверханомалии к обычным случаям аномалии вязкости, когда эффективная вяз­кость обратно пропорциональна напряжению сдвига.

участок (г-д) верхней ньютоновской области течения при напряжениях, превышающих напряжение сдвига предельного разрушения структуры.

Особенно отчетливо сверханомалии вязкости даже при небольшом сниже­нии температуры ниже пластовой (на 15 °С) наблюдаются у высокопарафини-стых узеньских нефтей. Причем это явление проявляется как после покоя, так и при непрерывном движении нефти.

Сверханомалии вязкости достаточно четко отмечаются у высокосмолистых нефтей залежей нижнего карбона Башкирии и Татарии после покоя, а также при температурах нефти, близких к температуре массовой кристаллизации парафина.

Для систем с такой формой линии консистентности Г.М. Бартенов и Н.В. Ермилова для исключения многозначности рекомендуют изображать зави­симость эффективной вязкости от градиента скорости, а не от напряжения сдви­га.

Выше было показано, что реологические свойства аномально вязких неф­тей можноохарактеризовать использованием четырех параметров -Мо, М_т>&>^Tm,a для нефтей со сверханомалией вязкости - введением дополни­тельно еще одного параметра Т^.