Уравнение состояния идеального газа

2.1. Состояние данной массы идеального газа описывается уравнением Менделеева - Клапейрона:

,

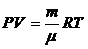где P,T - давление и температура газа; V - объем, занимаемый данной массой газа (объем сосуда); 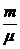- число молей, содержащихся в данной массе газа; R - универсальная газовая постоянная, R = 8,31Дж/(моль·K).

2.2. Исходя из уравнения состояния, можно определить плотность идеального газа:

.

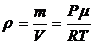Между температурой t (по шкале Цельсия) и температурой T (по шкале Кельвина) существует следующая связь:

T=(t + 273,15)К 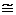(t+273) К.

2.3. Вводя постоянную Больцмана 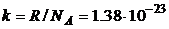Дж/К уравнение состояния (2.1) примет вид:

р = nkT,

где n – концентрация молекул.

2.4. Закон Дальтона для смеси газа.

Если в сосуде V при температуре T содержится смесь газов, то необходимо считать, что каждый из компонентов этой смеси распространяется по всему объему сосуда. Парциальное давление p_i, создаваемое отдельным i-м компонентом смеси, определяется из уравнения Менделеева - Клапейрона:

,

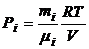где m_i- масса данного компонента в смеси; 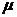_i - масса одного моля этого компонента.

Давление смеси газов равно сумме парциальных давлений, входящих в нее газов:

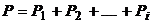
или

.

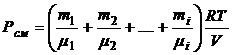В равновесном состоянии плотность смеси ρ_см равна сумме плотностей компонентов смеси:

.

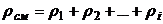Пример 1. Смесь азота и гелия при температуре 27⁰С находится под давлением Р = 1,3·10²Па. Масса азота составляет 70% от общей массы смеси. Найти концентрацию молекул каждого из газов.

Дано: Р=1,3·10²Па; m₁=0,7m; m₁ =28г/моль=28·10^-3кг/моль; 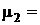4г/моль=4·10^-3 кг/моль; Т = 27+ 273 = 300К.

Найти: n₁ и n₂.

Решение. Давление смеси выразим по закону Дальтона:

.

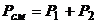где Р₁ – парциальное давление азота в смеси; Р₂ – парциальное давление гелия.

Выразим Р₁и Р₂ из уравнения Менделеева - Клапейрона:

; .

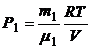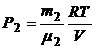Найдем соотношение между Р₁ и Р₂:

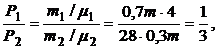т. е. Р₂ = 3Р₁.

Так как

Р_см = Р₁ + Р₂ = Р₁ + 3Р₁ = 4Р₁,

Следовательно,

, .

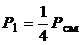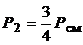С другой стороны, давление любого газа можно легко выразить через концентрацию его молекул (n) и температуру:

; .

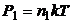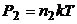Отсюда

; .

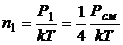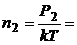
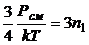Проверим размерность:

.

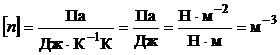Произведем вычисления:

;

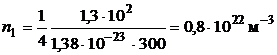n₂ = 3n ₁ = 2,4 ·10²² м^-3.

Ответ: n₁ = 0,8·10²² м^-3; n₂ = 2,4·10²²м^-3.

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ

ИДЕАЛЬНЫХ ГАЗОВ

3.1. Основное уравнение кинетической теории газов для давления:

,

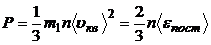где m₁ - масса одной молекулы; n – концентрация молекул; 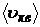- средняя квадратичная скорость молекул.

3.2. Средняя кинетическая энергия поступательного движения молекулы:

.

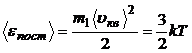(Эта формула раскрывает молекулярно – кинетическое толкование температуры: она – мера средней кинетической энергии поступательного движения молекул идеального газа).

3.3 Закон о равномерном распределении энергии по степеням свободы молекул: на каждую степень свободы приходится в среднем одинаковая энергия, равная

.

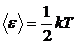3.4. Средняя энергия молекулы:

,

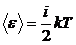где i - число степеней свободы молекулы данного газа: для одноатомных молекул i = 3 (поступательных), для двухатомных i = 5 (3 поступательных + 2 вращательных), для всех многоатомных i = 6 (3 поступательных + 3 вращательных).

3.5. Внутренняя энергия массы m газа:

.

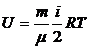3.6. Скорости газовых молекул:

· средняя квадратичная

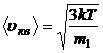или ,

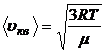· средняя арифметическая

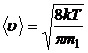или ,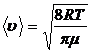

· вероятная

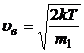или .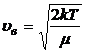

Пример 2. Найти среднюю квадратичную скорость, среднюю кинетическую энергию поступательного движения и среднюю полную кинетическую энергию молекул гелия и азота при температуре t = 27 ^оС. Определить полную энергию всех молекул каждого из газов. Массы газов одинаковы ( 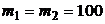г).

Дано: t = 27^оС; T=300 K; =100г = 100ּ10^-3кг; μ₁ = 4г/моль=4·10^-3кг/моль; i₁ = 3; μ₂ = 28г/моль = 28· 10^-3кг/моль; і₂ = 5.

Найти: 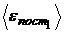; ; 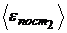; ; 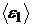; ; 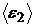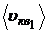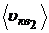U₁; U₂ .

Решение.1. Средняя кинетическая энергия поступательного движения одной молекулы при данной температуре T одинакова для любых молекул, т.е.

.

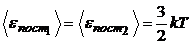2. Полная кинетическая энергия молекулы газа определяется по формуле:

,

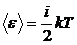тогда для молекул двух разных газов:

, .

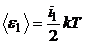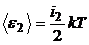3. Внутренняя энергия, заключенная в 100 г каждого из газов, определяется по формулам:

, .

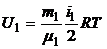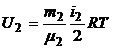4. Средняя квадратичная скорость молекул этих газов зависит от их молярной массы газа или от их масс, т.е.

, .

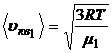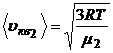Проверим размерность:

;

.

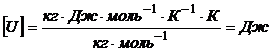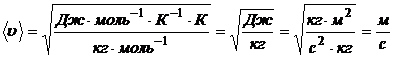Произведем вычисления:

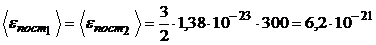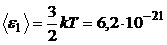Дж;

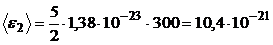Дж;

Дж;

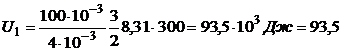
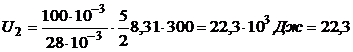кДж;

кДж;

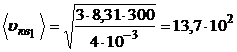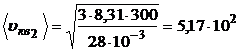м/с;

м/с.

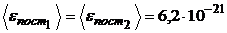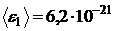Ответ: Дж; 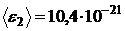Дж; Дж; ; ; ; .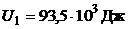

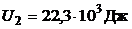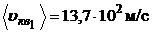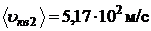4. ТЕПЛОЕМКОСТИ ИДЕАЛЬНОГО ГАЗА

4.1. Теплоемкость системы (тела):

,

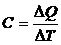где ∆Q – количество теплоты, сообщенное системе (телу); ∆Т – изменение температуры системы (тела), вызванное сообщением этого количества теплоты.

4.2. Молярная и удельная теплоемкости:

; .

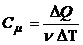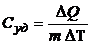4.3. Молярные теплоемкости идеального газа при постоянном объеме С_vμ и постоянном давлении С_рμ:

, .

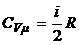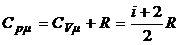4.4. Соотношение между молярной и удельной теплоемкостями:

.

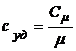4.5. Удельные теплоемкости идеального газа при постоянном объеме и постоянном давлении:

, .

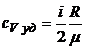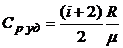4.6. Отношение теплоемкостей (показатель адиабаты):

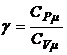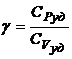или или .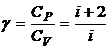

4.7. Количество теплоты, израсходованное на нагревание данного вещества: .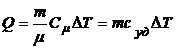

Пример 3. Вычислить удельные теплоемкости газа, зная, что его молярная масса µ = 4· 10^-3кг/моль и отношение теплоемкостей γ = 1,67.

Дано: μ = 4·10^-3 кг/моль; γ = 1,67.

Найти: с_Vуд, .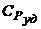

Решение. Исходя из классической теории теплоемкостей идеального газа, имеем:

, .

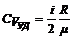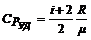Определим i из выражения:

,

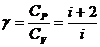отсюда

, .

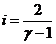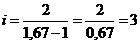Следовательно, газ одноатомный.

Проверим размерность:

.

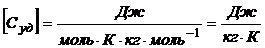Производим вычисления:

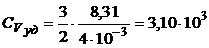Дж/(кг×К); 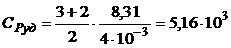Дж/(кг×К).