Характеристики физико-химических методов анализа

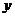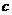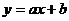На практике удобно использовать линейную зависимость от ; , Чувствительность. При выборе метода обнаружения и количественного определения вещества, желательно знать чувствительность данного метода. Чувствительность метода характеризуется минимально обнаруживаемой концентрацией, т.е. наименьшей концентрацией данного вещества, обнаруживаемого в данных условиях данным методом в единицах массы на единицу объема (мкмоль на л, мкг на мл). Предел чувствительности зависит от способов выполнения реакции и других факторов. Для количественной оценки чувствительности служит коэффициент чувствительности S:

;

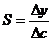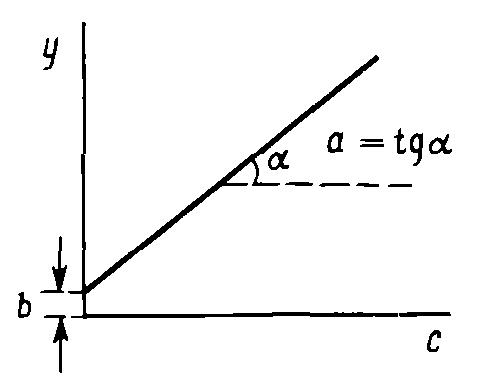
Рис.1 Градуировочный график

где 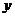- изменение измеряемого сигнала при изменении концентрации 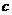. S – первая производная функции 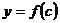. где 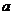- коэффициент чувствительности, равный тангенсу угла наклона прямой 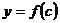, отсекающий отрезок 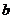по оси 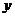; 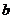- значение параметра 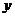в отсутствие определяемого компонента ( 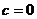). 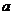и 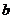можно вычислить методом регрессионного анализа. Если проведено 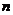-измерений параметра 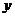при разных значениях 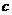, то по методу наименьших квадратов

,

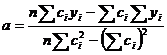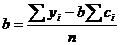
Если зависимость между 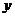и 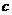не линейна, то стараются превратить её в линейную. Например, функцию типа 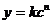можно привести к линейному виду логарифмированием:

.

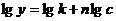В зависимости от чувствительности и количества материала методы ф/х анализа можно классифицировать как макро- (более 10^{-1 г), полумикро- (10-2}- 10^{-1 г), микро- (10-3}-10^{-2 г), ультрамикро- (10-7} – 10^{-4 г) и субмикрометоды (10-9} – 10⁷ г).

При анализе большого количества проб несколько различающихся по составу, значительную роль играет, с одной стороны воспроизводимость, т.е. близость полученных результатов к какой-то средней величине, а с другой стороны избирательность, т.е. возможность определения какого-то элемента в присутствии другого.

Критериями воспроизводимости служат отклонение d от среднего результата серии измерений 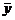и размах выборки .

Если разброс значений 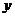можно описать нормальным распределением, то для оценки воспроизводимости обычно рассчитывают дисперсию V, стандартное отклонение S или относительное стандартное отклонение .

, ,

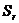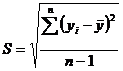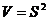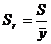
Предел обнаружения. 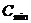- наименьшая концентрация, которую можно обнаружить с вероятностью .

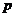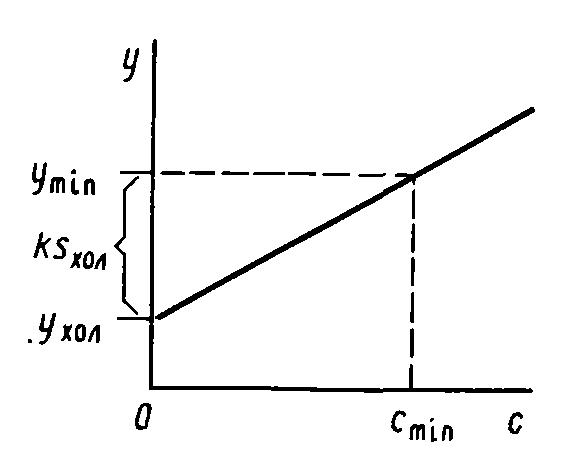
Рис.2 Связь между пределом обнаружения и минимальным аналитическим сигналом

Правильность – близость полученного и истинного значений измеряемой величины.

Оценка воспроизводимости и правильности анализа – необходимый этап при решении задач ф/х методами. Эти показатели существенно зависят от различных видов погрешностей при анализах. По своей природе ошибки могут быть грубыми систематическими и случайными.

Грубые ошибки (промахи) возникают, как правило, из-за невнимательности исследователя, временного выхода из строя измерительного прибора. Обычно такие ошибки проявляются при записи измеренной величины на фоне результатов анализов других проб. Для устранения грубых ошибок требуются повторные измерения.

Систематические ошибки – это односторонние (по знаку) погрешности, вызванные неисправностью измерительного прибора, недостатком метода. Систематические ошибки характеризуют правильность результата (например, если шкала прибора смещена на какую-то величину, то во все измерения будет входить одна и та же погрешность). Систематические ошибки связаны также с индивидуальными особенностями аналитика, с ошибками расчета (неправомочное округление чисел). Главным образом, систематические ошибки зависят от методических погрешностей. Источником методических ошибок может быть неоднородность анализируемого объекта, неадекватное применение метода анализа (например, применение методики определения фосфора в природной воде для определения фосфора в листьях растений), влияние примесей или основы анализируемого объекта, а также примесей в реагентах и растворителях.

Существуют определенные приёмы выявления систематических погрешностей, из них наиболее известных: 1) использование стандартных образцов; 2) варьирование массы навески; 3) метод добавок; 4) сравнение результатов анализа независимыми методами.

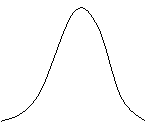
Случайные ошибки. В отличие от систематических погрешностей случайные ошибки не имеют видимой причины. Оценка случайных погрешностей проводится на основе математической статистики. К.Гаусс в начале прошлого века показал, что случайные ошибки подчиняются так называемому нормальному закону распределения, из которого следует: чем больше ошибка, тем реже она встречается, а положительные ошибки также вероятны, как отрицательные.

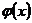
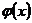- относительная вероятность

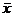- среднее значение

- +

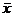
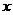
Рис. 1. Кривая плотности вероятности

нормально распределенной случайной

величины.

С_х

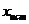
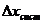
4 8 12

Рис. 2. Случайные и систематические погрешности при многократном анализе.

Случайные ошибки нельзя устранить. Их только можно свести к минимуму. Чем больше разброс данных при анализе, тем больше должно быть определений. Усреднение последних даёт результат измерений наиболее близкий к истинному.