Описание электронной оболочки многоэлектронного атома

Как уже отмечалось, строгое решение уравнения Шредингера возможно только для одноэлектронных частиц. По этой причине для описания электронных оболочек многоэлектронных атомов приходится прибегать к ряду упрощений и приближений.

Принцип водородного приближения. Согласно этому принципу электронную оболочку многоэлектронного атома можно описать набором орбиталей, а соответственно набором квантовых чисел атома водорода.

Принцип минимальной энергии - электроны заполняют орбитали в порядке увеличения их энергии.

В отличие от атома водорода, в многоэлектронном атоме реализуется межэлектронное отталкивание. Это взаимодействие является причиной двух эффектов, влияющих на распределение электронов в электронной оболочке.

Эффект экранирования ядра. В многоэлектронном атоме электроны внешнего электронного слоя испытывают отталкивание со стороны электронов более глубоких внутренних слоев, в результате чего энергия валентных электронов повышается, а их связь с ядром ослабевает. Так, для атома натрия ядро с зарядом +11 экранируют 10 электронов, находящихся на 1s-, 2s- и 2р-подуровнях. Если бы в атоме натрия имел место только эффект экранирования, на валентный электрон действовал бы заряд +1.

Эффект проникновения электрона к ядру. Вероятностная модель атома предполагает, что электрон может находиться на любом расстоянии от ядра, хотя и с разной вероятностью. Наиболее вероятное расстояние между ядром и электроном определяется положением главного максимума на кривой радиальной вероятности. Однако любой электрон, в том числе и валентный, часть времени пребывает на меньших расстояниях от ядра, как бы погружаясь во внутренние слои электронов. При этом энергия электрона уменьшается, а притяжение его ядром усиливается.

Кажущийся заряд ядра, соответственно которому ядро действует на внешние электроны, называется эффективным зарядом ядра (Z_эф):

Z_эф = Z - S,

где Z - истинный заряд ядра, а S - константа экранирования, значение которой определяется характером внутренних подуровней, заполненных электронами. Для атома натрия, например, Z_эф = 2,06 эл.ед.

Графики радиального распределения вероятности (рис. 2) наглядно показывают величину эффекта проникновения: чем больше максимумов, тем больше эффект. Число максимумов на кривой радиальной вероятности равно (n-l). В результате эффект проникновения электрона к ядру максимален для s-электронов, меньше для р-электронов и еще меньше для d-электронов. Поскольку проникновение электрона к ядру понижает энергию орбитали, энергия подуровней многоэлектронного атома при одинаковом значении n будет возрастать в ряду E_ns<E_np<E_nd....

Если сравниваемые подуровни принадлежат разным уровням, то для оценки их энергии необходимо одновременно учитывать главное и орбитальное квантовые числа. Оба эти фактора для большинства атомов позволяют учесть правила, сформулированные В.М. Клечковским: энергетические подуровни многоэлектронного атома заполняются электронами в порядке возрастания суммы главного и орбитального квантовых чисел; при равных значениях суммы (n + l) сначала заполняется подуровень с меньшим значением главного квантового числа.

Рассчитаем суммы (n + l) для орбиталей первых четырех энергетических уровней и определим порядок возрастания их энергии:

Уровень	Орбиталь	n	l	n + l	Уровень	Орбиталь	n	l	n + l
	1s					4s
4p
	2s				4d
2p				4f
	3s					5s
5p
3p				5d
3d				5f

Согласно правилам Клечковского энергия орбиталей будет увеличиваться в следующем порядке:

1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d...

Энергетическая диаграмма электронных орбиталей имеет вид:

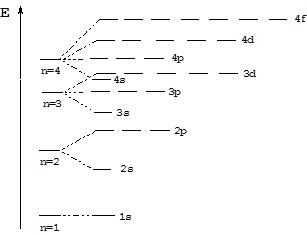
Принцип запрета Паули - невозможно существование двух электронов с одинаковым набором квантовых чисел. Квантовые числа n, l и m_l являются характеристикой орбитали и автоматически передаются ее электронам, а спиновое квантовое число электрона фиксировано (s = 1/2). Отсюда следует, что электроны, расположенные на одной орбитали, могут различаться только значением магнитного спинового квантового числа. Поскольку спиновое магнитное квантовое число электрона принимает два значения (m_s = ±1/2), на одной орбитали могут одновременно находиться только два электрона с разной ориентацией спина. Ограниченная емкость орбитали влечет за собой ограниченную емкость энергетических подуровней и уровней:

Подуровень	Число электронов	Уровень	Число Электронов
s		1 (K-слой)
p		2 (L-слой)
d		3 (M-слой)
f		4 (N-слой)

Правило Хунда - при заполнении энергетического подуровня электроны стремятся занять максимальное число орбиталей, ориентируя спин параллельно. Например, при реализации конфигурации p³ электроны занимают орбитали следующим образом:

Исходя из рассмотренных принципов, рассмотрим строение электронных оболочек атомов элементов периодической системы Д.И. Менделеева.

Первый периодпредставлен двумя элементами - водородом и гелием, у которых заполняется первый энергетический уровень.

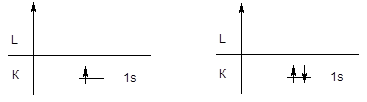
H 1s¹ He 1s²

При составлении электронной формулы атома или другой атомной частицы числом указывается главное квантовое число, буквой - орбитальное квантовое число и верхним индексом - число электронов на подуровне.

Поскольку емкость первого уровня ограничена двумя электронами, следующий элемент - литий начинаетвторой период, у элементов которого происходит последовательное заполнение второго энергетического уровня, начиная с конфигурации 1s²2s¹ (Li) и заканчивая конфигурацией 1s²2s²2p⁶ (Ne).

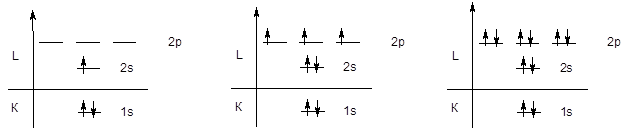
Li 1s²2s¹ . . . . . . N 1s²2s²2p³ . . . . . . . Ne 1s²2s²2p⁶

Аналогичным образом происходит заполнение s и p-подуровней третьего энергетического уровня у элементов третьего периода.

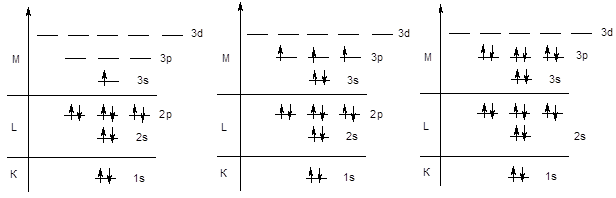
Na KL3s¹ . . . . . . P KL3s²3p³ . . . . . . Ar KL3s²3p⁶

Далее следовало ожидать заполнения орбиталей 3d-подуровня, однако у элементов четвертого периода начинается заполнение четвертого уровня, поскольку энергия 4s-подуровня ниже, чем энергия 3d-орбиталей - K (KL3s²3p⁶4s¹), Ca (KL3s²3p⁶4s²). После заполнения 4s-орбитали, в соответствии с правилами Клечковского, начинается заполнение 3d-подуровня. Поскольку d-подуровень вмещает 10 электронов, этот процесс охватывает 10 элементов от скандия до цинка.

Следует обратить внимание на то обстоятельство, что в электронной формуле указывается не порядок заполнения подуровней, а их конфигурация. Поэтому подуровень 3d записывается перед подуровнем 4s, хотя последний заполняется раньше.

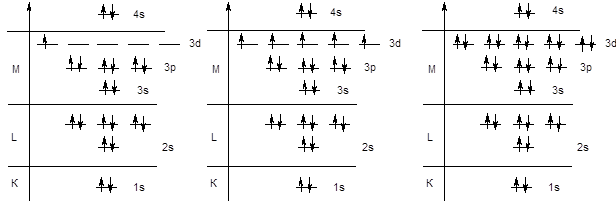
Sc KL3s²3p⁶3d¹4s² . . . . Mn KL3s²3p⁶3d⁵4s² . . . . Zn KL3s²3p⁶3d¹⁰4s²

Аналогичным образом происходит заполнение орбиталей атомов элементов пятого периода. У элементов шестого периода после заполнения подуровня 6s начинается заполнение 5d-орбиталей (La KLM4s²4p⁶4d¹⁰5s²5p⁶5d¹6s²) вместо ожидаемого заполнения подуровня 4f (нарушение правил Клечковского). Тем не менее, у последующих за лантаном элементов (лантанидов), происходит закономерное заполнение 4f-орбиталей от 4f² у церия до 4f¹⁴ у иттербия.

Нарушение ожидаемого порядка заполнения атомных орбиталей наблюдается в ряде мест периодической системы. Например, атом меди имеет электронную конфигурацию KL3s²3p⁶3d¹⁰4s¹ вместо ожидаемой KL3s²3p⁶3d⁹4s². Эта и аналогичные ей аномалии связаны со стремлением атома приобрести полностью (d¹⁰) или наполовину (d⁵) завершенный энергетический подуровень, обладающий повышенной устойчивостью. При этом электрон внешнего энергетического уровня как бы проваливается на предыдущий подуровень, что и обусловило название явления - провал электрона.

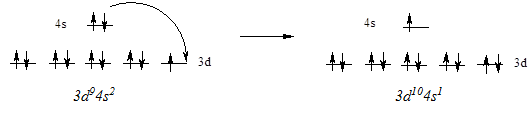
ХИМИЧЕСКАЯ СВЯЗЬ