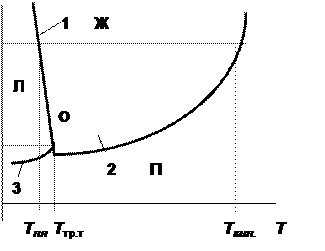Физико-химический анализ. Фазовые диаграммы

Изучение зависимости свойств многокомпонентных систем и их фазового состава от внешних факторов производится при помощи физико-химического анализа. Он заключается в изучении фазовых равновесий с помощью диаграмм состояния (фазовых диаграмм), на которых графически изображается состояние гетерогенных систем. (Понятие «физико-химический анализ» не следует путать с понятием «физико-химические методы анализа», которое применяется по отношению к аналитическим методам, связанным с использованием различных приборов - спектрофотометров, поляриметров, фотоколориметров и др.).

В основе физико-химического анализа лежат принципы непрерывности и соответствия, введённые Н.С.Курнаковым (1893 - 1902). Согласно принципу непрерывностипри непрерывном изменении параметров, определяющих состояние системы (давление, температура, концентрация компонентов), свойства её отдельных фаз изменяются также непрерывно до тех пор, пока не изменится число или характер фаз. При появлении новых фаз или исчезновении существующих свойства системы изменяются скачком.

Согласно принципу соответствиякаждой фазе или каждой совокупности равновесных фаз на диаграмме состояния соответствует опреде­лён­ный геометрический образ.

Диаграмма состояния(иначе - фазовая диаграмма) - это графическое изображение всех возможных фазовых состояний термодинамической системы в пространстве основных параметров состояния – температуры и давления (а для многокомпонентных систем и состава). На диаграммах состояния отображаются линии равновесия, разделяющие фазовые поля. Каждому реально существую­щему состоянию системы на диаграмме состояния отвечает определённая точка, называемая фигуративной. Если фигуративная точка находится внутри какого-либо фазового поля, это означает, что система, параметры которой соответствуют координатам фигуративной точки, находится в гомогенном (твёрдом, жидком или газообразном) состоянии. Если фигуративная точка находится на линии равновесия, то это значит, что при заданных её координатами параметрах система находится в гетерогенном состоянии, то есть в ней одновременно существуют в равновесии две фазы. В местах пересечения линий равновесия друг с другом имеются точки, отвечающие равновесию трёх или более фаз. В зависимости от вида диаграммы состояния эти точки носят различные названия, о которых будет сказано ниже.

Диаграмма состояния однокомпонентных систем обычно строится на плоскости в координатах давление - температура.

Диаграмма состояния воды

Рассмотрим диаграмму состояния однокомпонентной системы на примере воды (рис. 6.1).

р   1 атм     ртр.т.

Рис. 6.1. Диаграмма состояния воды

Фазовые поля, отвечающие области существования каждой из фаз (твёрдая вода - лёд Л, жидкая вода Ж и водяной пар П), отделены друг от друга линиями равновесия. В данном случае это линии плавления (1), испарения (2) и возгонки или сублимации (3). Каждая кривая равновесия может быть описана уравнением Клапейрона для соответствующего фазового перехода.

Вода по сравнению с другими веществами обладает довольно необычными свойствами. В частности, её твёрдая фаза имеет меньшую плотность, чем жидкая. Благодаря этому величина dp/dT для неё отрицательна и линия равновесия “лёд - вода” на диаграмме состояния воды имеет наклон в сторону оси давлений (отрицательный наклон).

Это обстоятельство сыграло особую роль в возникновении и развитии жизни на Земле, так как благодаря ему зимой лёд находится на поверхности морей, океанов и других водоёмов и экранирует собой жидкую воду, где живые организмы могут пережить холодное время года. Если бы величина dp/dT для воды была положительна, то лёд опускался бы на дно водоёмов и практически заполнил бы их доверху. Как показывают расчёты, тепла, получаемого летом от Солнца, не хватило бы для того, чтобы полностью расплавить лёд, находящийся под слоем воды. Таким образом, Земля была бы круглый год покрыта сплошным ледяным панцирем, и только летом на его поверхности мог бы образоваться тонкий слой жидкости, с наступлением зимы опять превращающийся в лёд. Поэтому живым организмам, даже если бы они смогли возникнуть в таких условиях, было бы невозможно сохраниться, будучи вмороженными в лёд, даже до следующего лета.

Для подавляющего большинства химических веществ величина dp/dT имеет положительный знак и для них линия равновесия “твёрдое тело - жидкость” на диаграмме состояния имеет наклон в сторону от оси давлений (положительный наклон).

Все три линии равновесия сходятся в тройной точке(О), отвечающей равновесному сосуществованию трёх фаз. Тройная точка воды имеет координаты Т = 0,0098^оС (273,1598 К), p = 0,0060 атм (607,5 Па). Следует помнить, что одновременное существование в системе трёх фаз, отвечающих различным агрегатным состояниям воды (как и других веществ), при температуре и давлении, отвечающим координатам тройной точки, возможно только при отсутствии других веществ, например, воздуха.

Точка пересечения изобары, соответствующей нормальному атмосферному давлению 1 атм (1,013´10⁵ Па), с линией плавления 1 отвечает нормальной температуре плавления льда Т_пл (0^оС или 273,15 К), а точка пересечения её с линией кипения 2 – нормальной температуре кипения воды Т_кип (100^оС или 373 К). Эти две температуры фазо­вых переходов являются константами воды и лежат в основе температурных шкал Цельсия и Кельвина.

Применяя к рассмотрению воды правило фаз Гиббса, получаем такие значения вариантности системы:

а) Для каждого фазового поля:

С = К - Ф + 2 = 1 - 1 + 2 = 2

Система бивариантна, то есть каждая фаза в отсутствие других может существовать в широкой области температуры и давления, которые можно изменять независимо друг от друга.

б) Для линий равновесия:

С = К - Ф + 2 = 1 - 2 + 2 = 1

Система моновариантна, то есть, если мы задали температуру равновесия между фазами (температуру плавления или температуру кипения), то тем самым должно быть однозначно определено равновесное давление и наоборот. Например, когда мы устанавливаем какое-то произвольное давление, температура кипения сама собой примет строго определённое значение, изменить которое при данном давлении невозможно. То же относится к возгонке, плавлению и обратным им фазовым переходам.

в) Для тройной точки:

С = К - Ф + 2 = 1 - 3 + 2 = 0

Система нонвариантна (инвариантна). Иначе говоря, если в однокомпонентной системе в равновесии находятся три фазы, то мы не можем произвольно менять ни один из параметров равновесия даже в малой степени без того, чтобы одна (или две) из фаз не исчезли.

ГЛАВА 7