Измерение теплоемкости материалов

Цель работы: Экспериментальное определения теплоемкости материалов.

Оборудование: Весы, разновес, калориметр, цилиндр металлический с известной теплоемкостью, мензурка, нагреватель, крючок.

Краткая теория:

Все макроскопические тела и системы тел помимо механической энергии, обусловленной их движением и взаимодействием, обладают энергией, зависящей от их внутреннего состояния. Эту энергию, являющуюся энергией движения и взаимодействия между собой всех частиц, из которых состоит тело, называют внутренней.

К внутренней энергии, относится кинетическая энергия теплового движения молекул и атомов, входящих в состав данного тела, кинетическая энергия электронов, движущихся в атомах вокруг ядер, потенциальная энергия взаимодействий между собой молекул, атомов, электронов и ядер, нуклонов в ядре и т.д. В понятие внутренней энергии не входит кинетическая и потенциальная энергия данного тела как единого целого.

Внутренняя энергия однозначно определяется совокупностью параметров, характеризующих состояние данной системы, т.е. является однозначной функцией состояния этой системы.

Внутреннюю энергию принято обозначать буквой U.

В тепловых явлениях, протекающих при температурах, далеких от температур фазовых переходов, изменение внутренней энергии DU связано с изменением кинетической и потенциальной энергии молекул, а остальные компоненты внутренней энергии при этом не изменяются. Поэтому в подобных процессах можно считать, что внутренняя энергия тела равна сумме кинетических энергий хаотического теплового движения всех молекул относительно центра масс этого тела и потенциальных энергий взаимодействия всех молекул между собой.

При изменении состояния тела его внутренняя энергия изменяется. Например, при повышении температуры тела его внутренняя энергия увеличивается, так как увеличивается средняя кинетическая энергия движения молекул этого тела. С понижением температуры внутренняя энергия тела уменьшается.

Внутренняя энергия тел может изменятся различными способами. Например, внутренняя энергия изменяется при совершении механической работы внешними силами над данным телом при его деформации, а также без совершения работы, когда тело находится в контакте с другим елом (или средой), имеющим более высокую или более низкую температуру, чем данное тело.

Процесс изменения внутренней энергии тела без совершения механической работы называют теплообменом или теплопередачей. Существуют три вида теплопередачи: конвекция, теплопроводность и излучение.

При теплообмене не происходит превращение энергии из одного вида в другой. Процесс теплообмена состоит в том, что часть внутренней энергии от более горячего тела передается менее горячему телу (или среде).

Для характеристики процессов теплопередачи введено понятие количества теплоты называют величину, являющуюся количественной мерой изменения внутренней энергии тела в процессе теплообмена.

Необходимо помнить, что тело может отдавать или получать только энергию, а количество теплоты Q является лишь численным эквивалентом энергии, отданной или полученной телом в процессе теплообмена.

Количество теплоты зависит от рода процесса и не является функцией состояния системы.

Количество теплоты, необходимое для нагревания тела, происходящего без фазовых превращений (без изменения агрегатного состояния вещества):

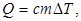(1)

где с - удельная теплоемкость тела, определяемая отношением количества переданной теплоты к массе m тела, и произошедшему при этом изменению температуры DT, m - масса тела, DT - разность конечной и начальной температур данного тела.

Количество теплоты, которое нужно сообщить телу, чтобы повысить его температуру на один Кельвин называется теплоемкостью этого вещества. При остывании на один Кельвин, тело отдает такое же количество теплоты. Теплоемкость тела пропорциональна массе тела и зависит от вещества, из которого оно состоит. В системе единиц СИ теплоемкость измеряется в Дж/К.

Для характеристики тепловых свойств вещества принимают теплоемкость единицы массы этого вещества. Эта характеристика называется удельной теплоемкостью. Она равна отношению теплоемкости данного тела к его массе. Удельная теплоемкость с системе СИ измеряется в Дж/(кг×К).

Экспериментально удельную теплоемкость металлического тела определяется при помощи калориметра и термометра. Простейший калориметр состоит из отполированного металлического стакана, поставленного внутри другого стакана на пробках (с целью тепловой изоляции). Внутренний стакан наполняется водой или другой жидкостью с известной удельной теплоемкостью. Тело, нагретое до определенной температуры t, опускают в калориметр. Пусть до опускания тела температура жидкости в калориметре была t_1, а после того, как установится тепловое равновесие жидкости и опущенного в него тела их общая температура станет равной q.

Из закона сохранения энергии следует, что:

Q = Q₁ +Q₂,, (2)

где количество теплоты Q, отданное нагретым телом, равно сумме количества теплоты Q₁, полученного водой, и Q₂, полученного калориметром.

Учитывая (1) перепишем (2) в виде:

сm(t-q) = c₁m₁(q-t₁) +c₂m₂(q-t₁), (3)

где c₁ и m₁ - удельная теплоемкость и масса воды в калориметре, c₂ и m₂ - удельная теплоемкость и масса калориметра. Это уравнение называется уравнением теплового баланса. Из него найдем удельную теплоемкость тела:

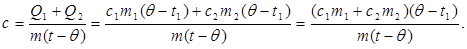(4)

Можно подойти к решению этой задачи по другому, предположим, что потери энергии в рамках одного эксперимента, будут одинаковы. Тело с известной удельной теплоемкостью, нагретое до определенной температуры t, опускают в калориметр, температура в котором изменяется. Тогда уравнение теплового баланса примет вид:

cm(t-q) = c₁m₁(q-t₁) + Q_потери,, (5)

где Q_потери - количество теплоты, получаемое калориметром и окружающей средой, следовательно:

Q_потери, = cm(t-q) - c₁m₁(q-t₁). (6)

Если тело с неизвестной удельной теплоемкостью, нагретое до той же температуры, опустить в калориметр, тогда уравнение теплового баланса примет вид:

c_x m_x (t-q_x) = c₁m¢₁(q - t¢₁) + Q_потери,, (7)

где m¢₁ - масса воды в калориметре, а t¢₁ - температура воды в данном эксперименте. Тогда:

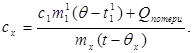(8)

Подставив значение (6) в (8) получим:

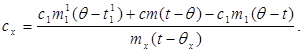(9)

Таблица 1.

Вещество	Удельная теплоемкость некоторых веществ. с, кДж/(кг×К)
Алюминий	0,92
Железо	0,46
Латунь	0,38
Медь	0,38
Никель	0,46
Олово	0,25
Свинец	0,13
Вода	4,2

Порядок выполнения работы

1. Сначала тело с известной удельной теплоемкостью (с) взвешивают на весах и определяют его массу (m).

2. Опускают это тело в нагреватель, где температура t = 100°С.

3. В калориметр наливают воду известной массы (m₁) и термометром измеряют ее температуру (t₁).

4. Нагретое, до температуры (t₁) тело с известной удельной теплоемкостью опускают в калориметр и определяют установившуюся температуру (q).

5. Тело с неизвестной удельной теплоемкостью взвешивают на весах и определяют его массу (m_x).

6. Опускают его в нагреватель с температурой (t = 100°C).

7. В калориметр наливают воду известной массы (m¢₁) и термометром измеряют ее температуру (t¢₁).

8. Затем нагретое до температуры (t) тело опускают в калориметр и определяют установившуюся температуру (q¢).

9. С помощью уравнения (9) находим неизвестную удельную теплоемкость.

10. Сравнивая полученный результат с табличными значениями определяем какое это вещество.

11. Все результаты вносим в таблицу (2).

12. Определим относительную погрешность искомой величины.

Таблица 2

№	m, кг	t, °С	t1, °C	q, °С	c1, Дж/(кгК)	m1, кг	t1¢, °С	m1¢, кг	qx, °С	cx, Дж/(кгК)

Относительную погрешность определим как:

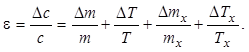
Контрольные вопросы

1. Сформулируйте уравнение теплового баланса.

2. Каков физический смысл удельной теплоемкости?

3. От чего зависит удельная теплоемкость вещества тела?

4. Можно ли в данной работе вместо воды использовать другую жидкость?

5. Из какого вещества изготовлено тело, удельную теплоемкость которого вы определили?

6. Как связать теплоемкость и удельную теплоемкость.

Литература

1. Савельев И.В. Курс общей физики. М.: Наука, 1977.т.1. С. 414.

2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 1973. т.1. С.607.

3. Зисман Г.А., Тодес О.М. Курс общей физики. М.: Высшая школа, 1974. т.1. С.507.

4. Трофимова Т.И. Курс физики. М.: Высшая школа, 1990. С.478.

5. Ахматов А.С. Лабораторный практикум по физике. М.: Наука, 1980. С.130.

6. Евграфова Н.Н., Каган В.Л. Руководство к лабораторным работам по физике. М.: Высшая школа, 1970. С.382.

Лабораторная работа № 4

Определение динамической вязкости жидкости
по методу Стокса.

Цель работы: Изучение транспортных свойств жидкостей. Определение коэффициента динамической вязкости жидкостей по скорости падения в них шарика.

Оборудование: стеклянный цилиндр, секундомер, шарики, линейка (шкала), микрометр, весы с разновесами, термометр.

Краткая теория:

Вязкость - это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой движущийся быстрее, действует тормозящая сила.

Сила внутреннего трения тем больше, чем больше рассматриваемая площадь поверхности слоев, и зависит от того, насколько быстрее меняется скорость течения жидкости при переходе от слоя к слою.

Рассмотрим течение жидкости между двумя горизонтальными бесконечно плоскими твердыми поверхностями, расположенными на расстоянии “a” друг от друга (рис. 1).

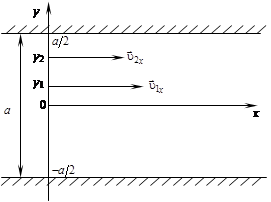Рис. 1.

В вязкой жидкости скорость ее течения будет зависит от координаты y (ось OY перпендикулярна горизонту). У твердых поверхностей скорость будет нулевой и касательной в плоскости, которой принадлежит ось OX.

Разобьем жидкость на слои параллельные плоскостям, настолько тонкие, что скорость течения жидкости по всей толщине слоя можно считать одинаковой. Пусть расстояние Dy = y₂ - y₁ между двумя некоторыми слоями, скорости которых соответственно n_2x n_1x. Для характеристики изменения скорости течения жидкости от координаты y принимается величина 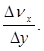Ее предел при 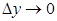называется градиентом скорости вдоль оси OY

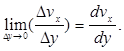(1)

Физический смысл этой величины состоит в том, что он численно равен изменению скорости течения жидкости в направлении оси ox при изменении координаты y на единицу длины. Очевидно, что единицей измерения градиента скорости будет с^-1. Изложенные выше рассуждения имеют место если, не происходит перемешивание слоев жидкости. Такое движение называется ламинарным.

При ламинарном течении сила F внутреннего трения пропорциональна градиенту скорости 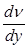и площади поверхности взаимодействующих слоев S:

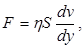(2)

где h - коэффициент зависящий от природы жидкости, коэффициент внутреннего трения (коэффициент динамической вязкости).

В системе СИ единицей динамической вязкости является Па×с.

В некоторых случаях вместо определенной выше динамической вязкости удобнее пользоваться кинематической вязкостью - отношением динамической вязкости жидкости к ее плотности:

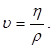(3)

Иногда вязкость растворов характеризуют относительной вязкостью - отношением вязкости раствора к вязкости растворителя.

Вязкость жидкости зависит от температуры: она резко уменьшается с повышением температуры. Особенно сильно зависит от температуры вязкость масел. Так, например, вязкость касторового масла при повышении температуры от 18 до 40°С падает почти в 4 раза. Поэтому, знание такой характеристики как вязкость крайне необходима в широком диапазоне температур для различных жидкостей.

Методы определения вязкости разнообразны. Один из наиболее простых методов является метод Стокса, который применяется для маловязких жидкостей.

Пусть шарик падает в некоторой жидкости. На него действуют три силы:

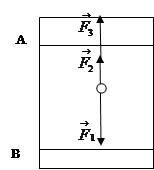Рис. 2.

1)сила тяжести F₁=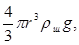

2)архимедова сила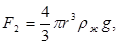

3)сила вязкого трения 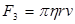(формула Стокса).

В формулах r - радиус шарика, r_ш - плотность шарика, r_ж - плотность жидкости, v - скорость шарика, h - коэффициент вязкости.

Сила вязкого трения зависит от скорости движения шарика. При свободном падении шарика в вязкой жидкости наступает момент с которого шарик движется равномерно и прямолинейно. Такое движение шарика называется установившимся. В соответствии с законами классической динамики это возможно при условии:

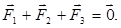(4)

В проекции на направление движения шарика:

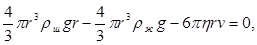(5)

Решим это уравнение относительно h

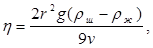(6)

где v = l/t, т.к. для средней части сосуда, ограниченной рисками А и В, где движение равномерное, l - расстояние, t - время падения шарика между рисками А и В. Подставим выражение для скорости в уравнение (6) тогда:

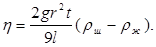(7)

Уравнение (7) справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиуса R, то приходится учитывать влияние боковых стенок. Поправку в формуле Стокса для такого случая теоретически обосновал Ладенбург. Формула для определения коэффициента вязкости с учетом поправок имеет вид:

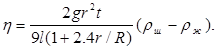(8)

Таблица №1 Плотность некоторых веществ, r×10³ кг/м³, (при 293К)

Вещество	Плотность
Железо	7,8
Никель	8,.8
Олово	7,3
Свинец	11,4
Сталь	7,9
Масло	0,9
Глицерин	1,26
Вода

Таблица №2 Динамическая вязкость, h×10^-3 кг/(м×с).

Вещество	h при t = 0°C	h при t = 10°C	h при t = 20°C
Вода	-	1.304	1.002
Глицерин
Масло касторовое	-

Порядок выполнения работы;

1. С помощью миллиметровой шкалы измерить расстояние между метками А и В.

2. Измерить диаметр шарика не менее трех раз. Найдя диаметр, как среднее арифметическое из трех измерений, результат записать в таблицу.

3. Измерить массу шарика и вычислить плотность, значение которой записать в таблицу.

4. Опустить шарик в жидкость, включить секундомер в момент прохождения шариком метки А, остановить секундомер в момент прохождения шариком метки В. Измеренное время записать в таблицу.

5. Измерьте диаметр D трубки, в которой падает шарик и запишите его в таблицу.

6. Повторить опыт от 3 - до 5 раз с разными шариками.

7. Вычислить вязкость жидкости.

8. Определить среднее значение динамической вязкости и вычислить кинематическую вязкость при данной температуре. Окончательный результат записать обязательно, указывая температуру жидкости.

9. Найти среднюю абсолютную ошибку измерения как:

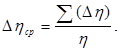
10. Найти относительную ошибку как:

.

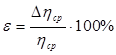11. Окончательный результат записать в виде:

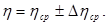
Таблица №3.

№	d, м	t, с	l, м	T, °C	g, м/c2	rш, кг/м3	rж, кг/м3	D, м	h, Па×с	hср, Па×с	n

Контрольные вопросы.

1. Объяснить механизм возникновение вязкого трения.

2. Какие физические величины характеризуют вязкое трение. Их физический смысл.

3. Вывод расчетной формулы.

4. Какие методы определения вязкости Вам известны и чем они отличаются. Содержание этих методов.

5. Определение динамической вязкости.

6. Определение кинематической вязкости.

7. Связь между динамической и кинематической вязкостью.

8. В каких единицах измеряется вязкость?

9. Как изменяется вязкость жидкостей от температуры? Обоснуйте свой ответ.

Литература:

1. Савельев И.В. т.1 стр.102 - 107.1977.

2. Радченко И.В. Молекулярная физика. М.1965.

3. Стрелков С.П. Механика стр. 136 - 143. 1975.

4. Евграфова Н.Н., Каган В.Л. “Руководство к лабораторным работам по физике, 1970, с.63-92.

Лабораторная работа № 5

Определение коэффициента поверхностного
натяжения жидкости

Цель работы: освоить метод отрыва капли для вычисления коэффициента поверхностного натяжения жидкости

Приборы и принадлежности: бюретка с жидкостью в штативе, стакан, термометр, аналитические весы с разновесами, штангенциркуль

Краткая теория

Свойства жидкости можно представить, рассматривая потенциальную энергию молекулы, находящуюся внутри жидкости, по отношению к потенциальной энергии молекулы вне жидкости. Потенциальная энергия молекулы внутри жидкости меньше потенциальной энергии молекулы вне жидкости. Поверхностный слой жидкости находится в иных условиях, чем весь объем жидкости. Для перевода молекулы из жидкости наружу необходимо преодолеть определенный потенциальный барьер, т.е. совершить определенную работу. Средняя энергия теплового движения молекул недостаточная, что бы совершить эту работу, в результате чего жидкость сохраняет свой объем.

Если мысленно выделить в жидкости какую-либо молекулу, то нужно учесть действие на неё всех других молекул. Однако силы взаимодействия между молекулами быстро убывают с расстоянием, так что практически достаточно учесть действие лишь молекул, расположенных достаточно близко.

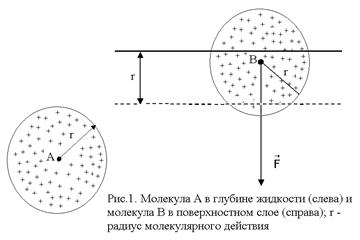
Пусть r- такое расстояние, что силы взаимодействия двух молекул, находящихся на расстоянии, большем, чем r, настолько малы, что ими можно пренебречь. Проведем вокруг молекулы A, как центра, сферу радиусом r. Тогда достаточно учесть действие на данную молекулу только тех молекул, которые находятся внутри сферы радиуса r.

Расстояние r принято называть радиусом молекулярного действия, а сферу радиуса r – сферой молекулярного действия.

В жидкости в сферу молекулярного действия, проведенную вокруг молекулы A, попадает большое число других молекул. Силы, с которыми эти молекулы действуют на молекулу A, направлены в различные стороны и в среднем компенсируются. Таким образом, результирующая сила, действующая на молекулу внутри жидкости со стороны других молекул, в среднем равна нулю. Иначе обстоит дело с молекулами, находящимися у поверхности жидкости. Рассмотрим молекулу B, расположенную от поверхности жидкости на расстоянии, меньшем радиуса молекулярного действия r. Тогда сфера молекулярного действия, как видно на рис.1, лишь частично окажется внутри жидкости, часть же её будет лежать вне жидкости. Пусть над поверхностью жидкости находится вещество в газообразном состоянии, например, пар данной жидкости. Концентрация молекул в паре мала, поэтому их действием можно вообще пренебречь. Следовательно, можно принять во внимание действие на молекулу B лишь молекул, лежащих в той части сферы действия, которая расположена внутри жидкости. При этом на молекулу B действует с разных сторон неодинаковое число молекул. Силы, с которыми они действуют на молекулу B, в среднем не будут компенсированы, возникает результирующая сила 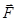, направленная внутрь жидкости. Таким образом, на каждую молекулу, лежащую от поверхности жидкости на расстоянии, меньшем радиуса молекулярного действия r, со стороны других молекул действует сила, направленная внутрь жидкости. На весь слой, лежащий у поверхности жидкости, действуют силы, направленные нормально к поверхности жидкости. Поверхностный слой оказывает на всю жидкость давление, называемое молекулярным давлением. Под влиянием этого давления молекулы жидкости оказываются сближенными, что ведет к появлению между ними сил отталкивания, уравновешивающих силы сжатия, вызванные поверхностным слоем.

Силы молекулярного притяжения направлены внутрь массы жидкости и при отсутствии других сил равновесным окажется такое положение поверхности, при котором эти силы нормальны к поверхности. Масса жидкости, при отсутствии действия на неё внешних сил, должна принять сферическую форму. Поэтому, переход данной массы жидкости от какой-либо несферической формы к сферической связан с уменьшением её поверхности. Следовательно, действие сил молекулярного давления аналогично действию, которое возникало бы, если поверхность жидкости представляла бы собой растянутую пленку, стремящуюся сжаться. Все явления, которые вызваны существованием молекулярного давления, объясняются путем рассмотрения действия такой растянутой пленки.

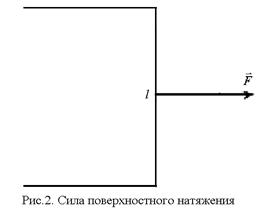
Для того чтобы растянутую пленку удержать в равновесии, нормально к линии её границы (рис.2) надо приложить силу 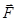, касательную к поверхности жидкости, называемую силой поверхностного натяжения. Эта сила, очевидно, тем больше, чем больше длина границы пленки l:

F=σl. (1)

Коэффициент σ, зависящий от природы жидкости, называется коэффициентом поверхностного натяжения. Из (1) можем получить:

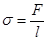. (2)

Таким образом, коэффициент поверхностного натяжения σ численно равен силе, приходящейся на единицу длины контура поверхностной пленки жидкости. Единица измерения σ в СИ Н/м :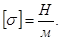

Для данной жидкости σ зависит от температуры: с повышением температуры он убывает (табл.1). При приближении температуры жидкости к критической температуре Т_кр коэффициент поверхностного натяжения σ стремится к 0, так как в этой точке разница между жидким и газообразным состояниями пропадает.

Таблица 1	Поверхностное натяжение воды в интервале температур 0-310С
t, ºC	σ, Н/м	t, ºC	σ, Н/м
	0,07549		0,07311
	0,07535		0,07295
	0,07520		0,07282
	0,07505		0,07265
	0,07490		0,07252
	0,07475		0,07235
	0,07460		0,07222
	0,07445		0,07208
	0,07430		0,07193
	0,07415		0,07178
	0,07401		0,07163
	0,07385		0,07148
	0,07370		0,07133
	0,07355		0,07118
	0,07341		0,07103
	0,07325		0,07088

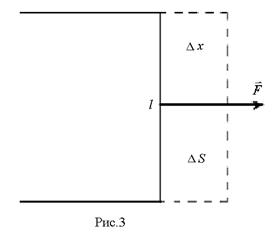
Определим работу, которую надо затратить, чтобы увеличить площадь поверхностной пленки жидкости на некоторую величину ∆S. Для этого с помощью силы 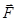передвинем границу пленки l на отрезок ∆x параллельно самой себе (рис.3). Совершенная при этом работа A равна A=F∆x=σl∆x=σ∆S, где ∆S- увеличение площади пленки. Эта работа идет на увеличение энергии пленки ∆E, откуда

∆E= σ ∆S (3)

или 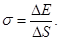(4)

Энергия Eпредставляет собой ту часть внутренней энергии пленки, которая может быть превращена в работу при изотермическом процессе. В термодинамике эту часть энергии называют свободной энергией. Из равенства (4) получаем ещё одно определение коэффициента поверхностного натяжения: коэффициент поверхностного натяжения σ численно равен отношению изменения свободной энергии поверхностной пленки к изменению площади этой пленки. Следовательно, 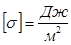. Поверхностное натяжение объясняет многочисленные явления, характерные для жидкого состояния вещества, например, образование капель при вытекании жидкости сквозь малые отверстия, образование пены, возникновение добавочного давления под выпуклой и вогнутой поверхностью жидкости, смачивание и не смачивания жидкостью твердого тела, капиллярные явления.

Упражнение 1. Определение коэффициента поверхностного натяжения методом отрыва капли

Для измерения коэффициента поверхностного натяжения рассмотрим образование капли при медленном вытекании жидкости из вертикальной трубки. Поверхностное натяжение не позволяет жидкости сразу вылиться из трубки. По мере вытекания жидкости поверхностная пленка капли получает сужение, или шейку. Сужение потом разрывается, и нижняя часть жидкости дает основную падающую каплю, а из сужения получается добавочная маленькая капелька (рис.4). При очень малом отверстии и недостаточном давлении со стороны жидкости капля может вообще не оторваться (мелкосетчатые поверхности, ткани и т.п.)

Условием отрыва капли является равенство её веса силе поверхностного натяжения, удерживающей каплю от падения:

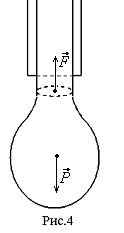P=mg=F=σl=2σπr, (5)

где m – масса капли,

g – ускорение свободного падения,

σ – коэффициент поверхностного натяжения,

r – радиус шейки капли,

l – периметр шейки капли в момент отрыва.

Следовательно, из равенства mg=σ2πr получаем расчетную формулу для σ:

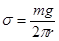(6)

За радиус шейки капли принимают внутренний радиус пипетки (капилляра).