Из уравнения (3) с учетом (1) и (2) получим
Fтр = ( 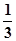 ρ
ρ 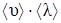 )
) 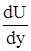 S = h
S = h 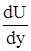 S
S
Откуда следует, что динамическая вязкость газа определяется по
η = 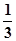 ρ
ρ 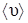
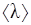 (4)
(4)
Для наблюдения явления переноса – внутреннее трение – необходимо создать условие для ламинарного течения газа. Ламинарное течение газа можно обеспечить при движении газа в трубках малого диаметра (капиллярах). Объёмный расход газа Q, проходящий через такой капилляр, определяется по формуле Пуазейля:
Q = 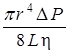 ,
,
где L и r – длина и радиус капилляра соответственно, м;
DР – перепад давлений на капилляре, Па.
Отсюда:
η = 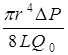 (5)
(5)
Из (4) находим среднюю длину свободного пробега молекул:
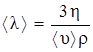 (6)
(6)
Средняя скорость теплового движения молекул:
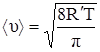 , (7)
, (7)
где R¢ = R/M –газовая постоянная;
R – универсальная газовая постоянная;
T - абсолютная температура;
М - молярная масса газа.
Плотность газа найдем из уравнения состояния
ρ = 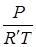 , (8)
, (8)
где Р – давление воздуха, Па.
Подставляя выражения (5), (7) и (8) в (6), получим:
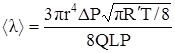 (9)
(9)
Разность давлений ΔP может быть измерена дифференциальным манометром, соединённым с капилляром.
Эффективный диаметр молекулы определяется по формуле:
d = 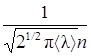 (10)
(10)
где n – число молекул в единице объёма при данных условиях.
Число молекул в единице объёма при данных условиях выражается формулой:
n = n0 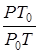 , (11)
, (11)
где n0 – число Лошмидта (число молекул в единице объёма при нормальных условиях, т.е. при T0 = 273К, P0 = 760 мм рт. ст.).
Из формул (8) и (9) получим выражение для эффективного диаметра молекулы воздуха:
d = 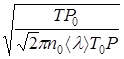 (12)
(12)
Описание установки
Для определения средней длины свободного пробега и эффективного диаметра молекул воздуха используется установка, состоящая из реометра (А) и капилляра (1) c манометром (Б) (рис.2).
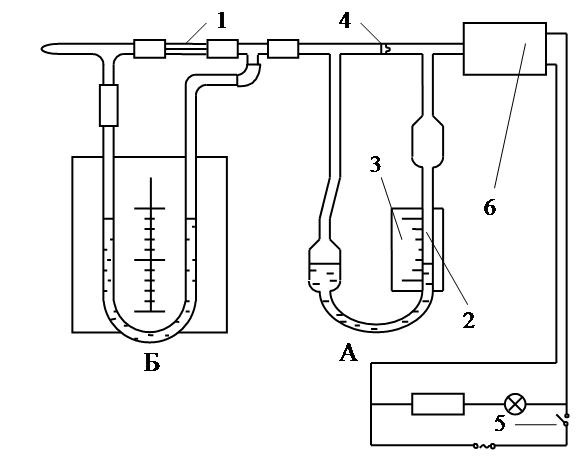 |
Рис.2. Схема установки для определения динамической
вязкости воздуха
Реометр стеклянный лабораторный типа РДС предназначен для измерения расхода газа в лабораторных условиях. Он состоит из дифференциального манометра (2), шкалы (3) и диафрагмы (4). Предельное допустимое значение избыточного давления, при котором может эксплуатироваться реометр, не должно быть более 100 мм вод. ст.
Шкала реометра подвижна и перемещается параллельно продольной оси дифференциального манометра. Принцип работы реометра основан на определённой зависимости между расходом газа и разностью далений газового потока до и после диафрагмы. От компрессора воздух прогоняется через систему. При этом в капилляре (4) установится течение воздуха, обусловленное разностью давлений на его концах. В левом конце давление – атмосферное, в правом – создаваемое компрессором. Манометр (Б), снабжённый шкалой позволяет определить перепад давления ΔP на концах капилляра. Объемный расход воздуха Q, протекающего через капилляр, определяется реометром.
Порядок выполнения работы
1. Установить нулевое положение прибора, т.е. совместить уровень воды в дифференциальном манометре с нулевой отметкой шкалы, используя возможность шкалы перемещаться в вертикальном направлении.
2. Включить тумблером (5) компрессор (6).
3. Снять показания по шкале реометра (в л/мин.) и по шкале манометра (в мм. вод. ст.).
4. Опыт повторить пять раз.
5. Записать температуру toC по комнатному термометру (Т = 273 + toC) и атмосферное давление по барометру Р (1 мм. рт. ст. = 133,3 Па)
6. Записать показания реометра и манометра в системных единицах измерений (м3/с , Па ).
7. Заполнить таблицу.
8. Найти длину свободного пробега молекул воздуха по формуле (9).
9. Для каждого опыта оценить относительную погрешность, предварительно пролагарифмировав и продифференцировав выражение (9).
10. Окончательный результат записать в виде:
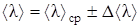
11. По среднему значению средней длины свободного пробега молекул воздуха по формуле (12) определить эффективный диаметр молекул.
12. Вычислить коэффициент внутреннего трения по формуле (5).
13. Вычислить погрешности определения величин h, d и 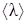 .
.
Таблица
| № | Q, м3/с | ΔP, Па | T, К | P, Па | 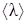 , м , м | h, Па×с | d, м |
| Среднее значение |
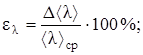 ed =
ed = 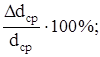 εη =
εη = 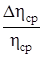 ∙100%
∙100%
Примечание:
R = 8,31 ∙ 103 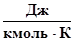 ; Mвоз =28,96
; Mвоз =28,96 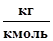 ;
;
n0 = 2,69 ∙ 1025 м-3.
Радиус r и длины капилляра L даются в лаборатории.
Контрольные вопросы
1. Дать описание процессу вязкости.
2. Записать закон вязкостного трения Ньютона.
3. От каких параметров зависит динамическая вязкость газа?
4. Объясните почему динамическая вязкость газа практически не зависит от давления и плотности газа при изотермических условиях?
5. Как влияет температура газа на его динамическую вязкость?
6. Что такое длина свободного пробега и эффективный диаметр молекул?
7. Как влияет давление газа на длину свободного пробега молекул?
8. Получите и объясните уравнение Пуазейля для вязкости.
9. Рассказать принцип работы реометра.
Литература
1. Савельев И.В. Курс общей физики т.1 М.: Наука, 1989 с. 274–287.
2. Детлаф А.А., Яворский Б.М. Курс физики М.: Высш. шк., 2002. с. 136–143.
3. Зисман Г.А., Тодес О.М. Курс общей физики, т.1 «Наука» 1972г. с. 128–134.
Таблица
| № | V0 | ΔP | T | P | 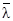 | η | d |
| м3/с | Па | К | Па | м | м2/с | м | |
| 1. | |||||||
| 2. | |||||||
| 3. | |||||||
| 4. | |||||||
| 5. | |||||||
| Среднее значение |
ελ = 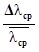 ∙100%
∙100%
εd = 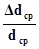 ∙100%
∙100%
εη = 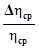 ∙100%
∙100%
Примечание:
R = 8,31 ∙ 103 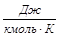 ; μвозд = 28,96
; μвозд = 28,96 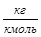 ; n0 = 2,69 ∙ 1025 м-3
; n0 = 2,69 ∙ 1025 м-3
Величины радиуса r и длины капилляра L даются в лаборатории.
Контрольные вопросы
1. Дать описание процессу вязкости.
2. Записать закон вязкостного трения Ньютона.
3. От каких параметров зависит динамическая вязкость газа?
4. Объясните почему динамическая вязкость газа практически не зависит от давления и плотности газа при изотермических условиях?
5. Как влияет температура газа на его динамическую вязкость?
6. Что такое длина свободного пробега и эффективный диаметр молекул?
7. Получить и объяснить уравнение Пуазейля для вязкости.
8. Рассказать принцип работы реометра.
Литература
1. Савельев И.В. Курс общей физики т.1 М.: Наука, 1989 с 274-287.
2. Детлаф А.А., Яворский Б.М. Курс физики М.: Высш. шк., 2002. с 136–143.
3. Зисман Г.А., Тодес О.М. Курс общей физики, т.1 «Наука» 1972г. с. 128-134.
Лабораторная работа № 3.
