Для молярных теплоемкостей идеального газа получим формулу Майера
СР - СV = R .
Адиабатным процессом называется такой термодинамический процесс, в котором к системе не подводится и от системы не отводится теплота, т.е.
dQ = 0
Термодинамическую систему, в которой протекает адиабатный процесс, можно представить себе в виде некоторого объема, ограниченного оболочкой с идеальной тепловой изоляцией, не пропускающей теплоту. Такая оболочка называется адиабатной. В реальных условиях процесс можно считать адиабатным, когда система снабжена хорошей теплоизоляцией, или когда процесс протекает настолько быстро, что система не успевает вступить в теплообмен с окружающей средой (например, при быстром сжатии и расширении газа).
Первый закон термодинамики для адиабатного процесса для массы вещества 1 кг приобретает следующий вид:
du = – Рdυ; (5)
di = υdР (6)
Из уравнений (5) и (6) получим:
 , (7)
, (7)
где γ – безразмерная величина называется показателем адиабаты или коэффициентом Пуассона.
Дифференциальное уравнение адиабатного процесса (адиабаты) можно представить в следующем виде
dlnР + γ dlnυ =0. (8)
Если показатель адиабаты принять постоянным, то дифференциальное уравнение (8) в следующее:
d(ln(Рυγ) = 0
Интегрируя это уравнение, получим:
ln(Рυγ) = lnconst
Или
Рυγ = const; (9)
для любой массы вещества объемом V уравнение (9) имеет вид
РVγ = const.
Уравнение (9) называется уравнением адиабаты или уравнением Пуассона и справедливо и для газа, и для жидкости, и для твердого тела. Если показатель адиабаты изменяется с изменением состояния системы, то можно использовать среднее значение показателя γср.
Реальные газы в области умеренных давлений по своим свойствам приближаются к идеальным газам и для них можно применять соотношения для идеальных газов. Для идеального газа показатель адиабаты с учетом соотношения (7) определяется по формуле:
γ = ср/сv = Cp/Cv = 1+R/Cv 
Приборы, необходимые для выполнения работы
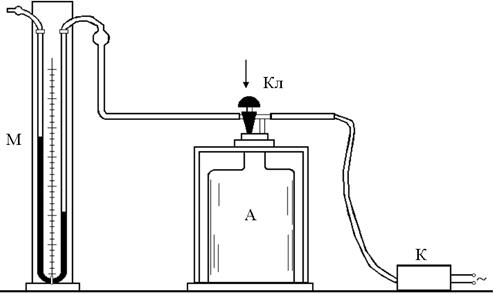
Прибор Клемана – Дезорма, с помощью которого можно определить величину  (рис.1). Он представляет собой баллон A с воздухом, накачиваемым компрессором K, до некоторого давления P, избыток которого DР = Р – Р0 над атмосферным р0 определяется по водяному манометру, соединённому с баллоном шлангом,
(рис.1). Он представляет собой баллон A с воздухом, накачиваемым компрессором K, до некоторого давления P, избыток которого DР = Р – Р0 над атмосферным р0 определяется по водяному манометру, соединённому с баллоном шлангом,
DР = rgh
Для осуществления быстрого (адиабатного) расширения воздуха из баллона в атмосферу служит ручной клапан Кл.
Выделим (мысленно) внутри воздуха, находящегося в баллоне А, некоторую массу газа m и проследим за изменением её состояния во время опыта при одновременном изменении давления Р и температуры Т.
Если клапан Кл открыт, то давление в сосуде равно атмосферному Р0; температура воздуха в сосуде равна T0 – температуре окружающей среды. Тогда параметрами мысленно выделенной массы воздуха будут V0, P0, T0, где V0 – объём рассматриваемой массы воздуха при давлении P0 и температуре T0.
Если теперь закрыть клапан Кл и накачать с помощью компрессора в сосуд некоторое количество воздуха, то рассматриваемая нами масса воздуха сожмётся, а температура и давление её повысятся. Через некоторое время, вследствие теплообмена с окружающей средой, температура воздуха в сосуде станет равной T0. Давление же будет равно:
P1 = P0 + rgh1, (10)
где h1 – окончательная (после установления теплового равновесия с окружающей средой) разность уровней жидкости в манометре.
Состояние рассматриваемой массы воздуха определяется теперь параметрами V1, P1, T0 – это 1-ое состояние выделенной массы воздуха; V1 – объём рассматриваемой массы воздуха при давлении P1 и температуре T0.
Если на короткое время (~ 1÷2 с) открыть клапан Кл (рис. 1), то воздух, находящийся в баллоне, быстро (адиабатно) расширится и вследствие этого охладиться. В конце этого малого промежутка времени, в течение которого клапан Кл открыт и баллон сообщается с атмосферой, давление воздуха внутри сосуда станет равным давлению атмосферы P0, и состояние рассматриваемой массы воздуха будет определяться в этот момент следующими параметрами:
V2, P0, T1 – 2-ое состояние выделенной массы воздуха, где V2 – объём выделенной массы воздуха. При этом T1 < T0.
|
Когда давление в сосуде А сделается равным давлению атмосферы (~ 1÷2 с) клапан Кл закрывают. Воздух, находящийся в баллоне, начнёт нагреваться от T1 до T0 вследствие получения тепла от окружающей среды, давление в сосуде начнёт повышаться и станет равным:
P2 = P0 + rgh2, (11)
где h2 – разность уровней жидкости в манометре после того, как температура газа в баллоне станет равной температуре окружающей среды.
Рассматриваемая масса воздуха теперь характеризуется параметрами V2, P2, T0 – это 3-е состояние рассматриваемой массы воздуха.
Итак, рассматриваемая масса воздуха во время опыта находилась последовательно в трёх состояниях:
1. V1, P1, T0
2. V2, P0, T1
3. V2, P2, T0
Переход из первого состояния во второе происходит адиабатно, а точки состояний 2 и 3 лежат на изохоре.
На рис.2 изображены графики процессов: кривая 1-2 – адиабата, кривая 2-3 – изохора, кривая 1-3 – изотерма.
Газ в состояниях 1-3 имеет одинаковую температуру T0.
Переход из состояния 1 в состояние 2 описывается уравнением Пуассона:
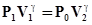 . (12)
. (12)
 |
Параметры 1-го и 3-го состояний удовлетворяют закону Бойля – Мариотта:
P1V1 = P2V2 . (13)
Возведя уравнение (13) в степень γ и разделив его почленно на (12), получим
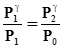 ,
,
отсюда
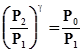 . (14)
. (14)
Учитывая равенства (9) и (10), получаем, что
P0 = P1 – rgh1, P2 = P1 – rg(h1 - h2)
и подставляя их в равенство (14), имеем
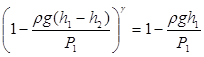 . (15)
. (15)
Так как rg(h1 – h2) << P1, то разложив левую часть (15) в ряд и ограничившись первым членом разложения, получим
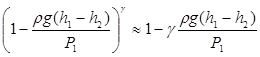 . (16)
. (16)
Приравняв правые части (14) и (15), получим следующую формулу:
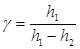 ,
,
которая используется в этой работе для экспериментального определения γ.
Порядок выполнения работы
1. При закрытом клапане Кл компрессором осторожно накачивают воздух в баллон А до разности уровней жидкости в манометре 30 – 35 см.
2. Выжидают 2 – 3 минуты, пока уровни жидкости в манометре не перестанут изменяться; затем отсчитывают их разность h1 с точностью до 1 мм.
3. Открыв клапан Кл выпускают из баллона воздух. Клапан остаётся открытым в течение 1-2 секунд, пока не прекратится шипение выходящего из баллона А воздуха, после чего клапан Кл закрывают.
4. Выжидают минуты 2 – 3, следя за изменением уровней жидкости в манометре; когда уровни установятся, берут отсчёт разностей уровней жидкости в манометре h2.
5. Опыт проделывают не менее десяти раз. Результаты измерений записывают в таблицу.
6. Рассчитать абсолютную и относительную погрешность полученного результата.
7. Окончательный результат записать в виде 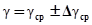 .
.
Таблица
| № измерения | Разность уровней жидкостей в манометре h1, мм | Разность уровней жидкости в манометре h2, мм | h1 – h2 , мм | 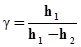 | Δγ |
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. | |||||
| 5. | |||||
| 6. | |||||
| 7. | |||||
| 8. | |||||
| 9. | |||||
| 10. | |||||
| Среднее |
Контрольные вопросы
1. Дайте определение удельной и молярной теплоёмкости при:
а) постоянном давлении;
б) постоянном объёме.
2. Выведите соотношение между теплоёмкостями при постоянном давлении и постоянном объеме.
3. Какие процессы изменения состояния воздуха имеют место в данной работе?
4. Чему равен показатель адиабаты γ в уравнении Пуассона? Каково его численное значение для одноатомного и многоатомного газов?
5. Вычислите теоретическое значение γ для воздуха, считая воздух идеальным двухатомным газом.
6. Какой процесс называется адиабатным? Выведите уравнение адиабатного процесса.
7. Какие процессы называются изохорным, изотермическим, изобарным? Нарисуйте в диаграмме P, V графики этих процессов.
8. Чему равна теплоемкость в изотермическом и адиабатном процессах?
9. Как меняется внутренняя энергия газа при адиабатном процессе?
10. Как меняется температура газа при адиабатном процессе?
11. Выведите формулу, выражающую зависимость молярной теплоёмкости идеального газа при постоянном давлении от числа степеней свободы молекулы.
Литература
1. Детлаф А.А., Яворский Б.М. Курс физики М.: Высш. шк., 2002. с. 114–125, 146-148.
2. Савельев И.В. Курс общей физики. Т.1. – М.: Наука, 1977, §§ 87, 88, 97.
3. Зисман Г.А., Тодес О.М. Курс общей физики. Т.1. – М.: Наука, 1972, §§ 32, 33.
Лабораторная работа № 2
Определение средней длины свободного пробега, эффективного диаметра молекул воздуха и динамической вязкости воздуха
Цель работы: Методом продувания воздуха через капилляр по динамической вязкостиопределить длину свободного пробега и эффективный диаметр молекул воздуха
Приборы и принадлежности: экспериментальная установка, барометр, термометр
Краткая теория работы
Состояние газа характеризуют основными параметрами: давлением P, температурой Т и объёмом V. Состояние вещества называется равновесным, если все его элементарные объемы имеют одинаковые параметры.
 |
При выводе вещества из состояния равновесия, возникают явления, стремящиеся вернуть его в прежнее или новое состояния равновесия. В основе этих явлений лежит один и тот же молекулярный механизм – тепловое поступательное движение молекул, которые переносят массу (диффузия), энергию (теплопроводность), и импульс (внутреннее трение).
Рассмотрим явление переноса импульса – внутреннее трение.
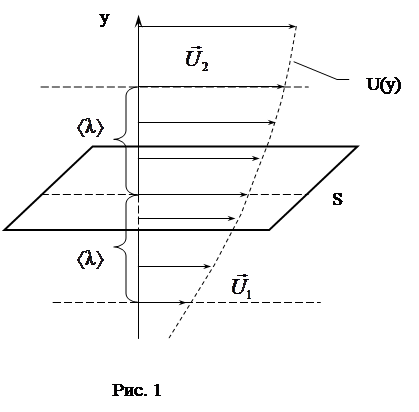
При изменении скорости U в потоке газа или жидкости вдоль координаты y на границе между двумя смежными слоями действуют сила внутреннего трения Fтр, величина которой при ламинарном режиме течения определяется по закону вязкостного трения Ньютона:
Fтр = η 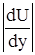 S, (1)
S, (1)
где h - динамическая вязкость (коэффициент внутреннего трения), Па×с;
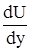 – градиент скорости, т.е. производная в направлении внешней нормали (ось у) к поверхности слоя;
– градиент скорости, т.е. производная в направлении внешней нормали (ось у) к поверхности слоя;
S – величина площади поверхности слоя, по которой действует сила Fтр .
Рассмотрим два слоя движущихся со скоростями U1 и U2 и находящихся от площади S на расстоянии средней длины свободного пробега молекул 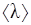 (среднее расстояние
(среднее расстояние 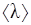 , которое проходит молекула при тепловом поступательном движении между двумя последовательными столкновениями). За единицу времени через поверхность S в направлении оси y из одного слоя в другой пройдёт количество молекул, равное
, которое проходит молекула при тепловом поступательном движении между двумя последовательными столкновениями). За единицу времени через поверхность S в направлении оси y из одного слоя в другой пройдёт количество молекул, равное
N = 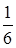 n
n 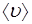 S,
S, 
где n – концентрация молекул, м–3;
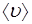 - средняя скорость теплового движения молекул.
- средняя скорость теплового движения молекул.
Умножив это количество молекул на импульс одной молекулы слоя, т.е. на m0U, получим импульс движущихся слоёв газа. В итоге импульс более быстро движущегося слоя (со скоростью U2) убывает, а более медленно движущегося (со скоростью U1) – возрастает.
Поток импульса через поверхность S на границе слоев
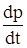 = Nm0 (U1– U2) =
= Nm0 (U1– U2) = 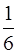 n
n 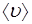 S m0(U1 – U2),
S m0(U1 – U2),
где n∙m0 = ρ – плотность газа.
Выражая разность скоростей слоёв через градиент скорости
U1 – U2 = – 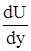 2
2 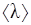 ,
,
получим
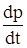 = –
= – 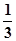 ρ
ρ 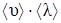 S
S 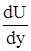 (2)
(2)
Согласно второму закону Ньютона сила трения равна производной импульса по времени
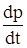 = – Fтр, (3)
= – Fтр, (3)
где Fтр – сила трения, возникающая между слоями, движущимися с разными скоростями.
Знак минус в уравнении обусловлен тем, что импульс «течет» в направлении убывании скорости U.
