Термодинамические функции состояния

УДК 541(075.8)

ББК 24.1

Рецензенты: кафедра общей и неорганической химии Санкт-Петербургского государственного политехнического университета (зав. каф., д-р. хим. наук, проф. Л.Н. Блинов); профессор кафедры физической химии Санкт-Петербургского государственного технологического института (университета) д-р. хим. наук Л.В. Пучков

Утверждено

редакционно-издательским

советом университета

ã БГТУ, СПб., 2003

ВВЕДЕНИЕ

Химия – наука, изучающая свойства и превращения веществ,сопровождающиеся изменением их состава и строения. Кроме учения о строении вещества, необходимо знание закономерностей процесса превращения одних веществ в другие, т. е. условий протекания химической реакции. При рассмотрении общих закономерностей протекания химических процессов необходимо ответить на два вопроса: 1) возможно ли и в каких пределах протекание химической реакции в данных условиях (температура, давление, состав реакционной смеси и другие факторы); 2) как быстро во времени будет осуществляться самопроизвольный процесс, т. е. какова скорость химической реакции.

Ответ на первый вопрос дает химическая термодинамика, задачи которой – определение возможности или невозможности самопроизвольного протекания процесса в том или ином направлении, условий химического равновесия, определение тепловых эффектов химических процессов.

Ответ на второй вопрос дает химическая кинетика, позволяющая определить факторы эффективного воздействия на скорость химического процесса и оптимальные условия его проведения.

Химическая термодинамика устанавливает энергетическую возможность химического превращения при заданных условиях, однако эта возможность может быть не реализована из-за ничтожно малой скорости протекания реакции. Таким образом, термодинамические условия осуществления процесса являются необходимыми, но не достаточными. Если показана термодинамическая невозможность протекания процесса, то он протекать не будет (достаточное условие). Но если термодинамика разрешает самопроизвольный химический процесс, то это не значит, что он будет протекать. Для того чтобы процесс протекал с заметной скоростью, необходимо выполнение кинетических условий.

Авторы выражают благодарность коллегам по кафедре, особенно профессору Б.Т. Плаченову и доцентам Т.Э. Кехва и Д.С. Маслобоеву за ценные замечания при обсуждении данного пособия. Авторы признательны профессорам Л.В. Пучкову, Л.Н. Блинову и Р.Г. Чувиляеву, взявшим на себя труд по рецензированию рукописи.

ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА

Термодинамика – наука, изучающая превращения (переходы) энергии из одной формы в другую, от одной части системы к другой, энергетические эффекты, сопровождающие физические и химические процессы, возможность, направления и предел самопроизвольного протекания процессов. Термодинамика изучает энергетические переходы макроскопических систем в целом, не вдаваясь в подробности, связанные с микроскопическим строением системы и "судьбой" отдельных, составляющих ее частиц. В отличие от теории строения вещества и химической связи, термодинамическому изучению подвергаются системы, состоящие только из большого (статистически значимого) числа частиц. Раздел термодинамики, в котором рассматриваются изменения энергии систем в ходе химических превращений, называется химической термодинамикой. Химическая термодинамика – термодинамика химических процессов.

1.1.Основные понятия и определения

Термодинамическая система

Термодинамическая система – это совокупность взаимодействующих между собой физических тел, выделенная из окружающего пространства реальной или мысленной границей. Остальная часть пространства является внешней (окружающей) средой.

Взаимодействие термодинамической системы с окружающей средой осуществляется путем обмена веществом и энергией.

В зависимости от свойств границ между термодинамической системой и окружающей средой выделяют системы:

· изолированные – отсутствует обмен веществом и энергией между системой и окружающей средой (dm=0;dE=0). При протекании процесса не меняются масса вещества и энергия системы.

· закрытые (замкнутые) – при протекании процесса происходит обмен энергией между системой и окружающей средой. Обмен массой вещества отсутствует (dm=0;dE¹0).

· открытые (незамкнутые) – при протекании процесса происходит обмен между системой и окружающей средой как энергией, так и веществом (dm ¹0;dE¹0).

Обмен энергией между термодинамической системой и окружающей средой может происходить как в виде передачи теплоты, так и путем совершения работы (рис.1.1).

Теплота – это форма передачи кинетической энергии атомов и молекул от одного тела к другому, которая может осуществляться тремя способами: при непосредственном их соприкосновении – теплопередачей, при самопроизвольном механическом перемешивании газов или жидкостей с различным значением энергии – конвекцией, при испускании и поглощении электромагнитного излучения – лучеиспусканием. Условно принято считать, что теплота, полученная от окружающей среды, положительна (dQ>0), а теплота, отданная системой, – отрицательна (dQ<0). Процессы, протекающие в системе без обмена теплотой с окружающей средой, называются адиабатическими (dQ=0).

Работа при взаимодействии с окружающей средой может совершаться как самой системой против внешних сил, так и внешними силами против системы. Условно принято считать, что в первом случае работа положительна (dW>0), а во втором – отрицательна (dW<0).

Рис. 1.1. Обмен энергией и веществом между термодинамической системой

и окружающей средой

В зависимости от состояния и свойств физических тел, образующих термодинамическую систему, различают гомогенные системы, все части которых обладают одинаковыми физико-химическими свойствами, и гетерогенные – системы, в которых можно выделить отдельные части, обладающие различными физико-химическими свойствами, т. е. состоящие из нескольких фаз (две и более). Фаза – совокупность частей системы, которые обладают одинаковыми физико-химическими свойствами и отделены друг от друга поверхностью раздела (граница фазы).

Примеры гетерогенных систем:

· монокристалл, находящийся в контакте с газом (обе фазы непрерывны и имеют различный химический состав);

· кусочки льда, плавающие на поверхности воды (лед – прерывная фаза; обе фазы имеют одинаковый химический состав);

· смесь кристаллов, полученная механическим смешиванием или при кристаллизации (обе фазы прерывны и имеют различный химический состав).

Совокупность всех физических и химических свойств системы называется ее состоянием, которое характеризуется термодинамическими параметрами. Термодинамическим параметром может быть любое свойство системы, если оно рассматривается как одна из независимых переменных. Число независимых параметров, необходимое и достаточное для полного описания состояния системы, называется числом термодинамических степеней свободы.

Параметры состояния, которые можно определить непосредственно, принято считать основными. К ним относятся температура (термодинамическая шкала Кельвина) T [K], давление р [Па = Н/м²], объем V [м³, л], количество вещества (число молей вещества) n, концентрация вещества C [мольная доля; моль/л].

Считается, что термодинамическая система находится в состоянии равновесия, если ни один из ее параметров не изменяется во времени и это состояние не поддерживается каким-либо внешним по отношению к системе воздействием. То есть одновременно выполняются следующие условия:

· давление во всех точках системы одинаково (механическое равновесие);

· температура во всех точках системы одинакова (термическое равновесие);

· химический и фазовый состав системы постоянен (химическое равновесие).

Примечание. Система, находящаяся в состоянии равновесия, называется стабильной. В ряде случаев в системе, находящейся в неравновесном состоянии, сохраняются во времени значения термодинамических параметров. Это связано с тем, что скорость перехода системы в состояние равновесия практически равна нулю. Такие системы называются метастабильными. Например, при комнатной температуре метастабильными системами являются алмаз или смесь газообразного водорода и кислорода. Очевидно, что при соответствующем внешнем воздействии системы самопроизвольно перейдут в стабильное состояние.

Параметры системы, находящейся в состоянии равновесия, находятся в функциональной зависимости: изменение одного из параметров должно сопровождаться изменением других параметров. Уравнения, связывающие термодинамические параметры системы в состоянии равновесия, называются уравнениями состояния.

Пример. Уравнение состояния n молей идеального газа – уравнение Менделеева-Клапейрона:

р×V =n×R×T.

Термодинамический процесс

Один из постулатов термодинамики формулируется так: термодинамическая система стремится перейти в состояние равновесия, в котором может находиться сколь угодно долго при отсутствии внешнего воздействия на нее.

Если на систему оказывается какое-либо внешнее воздействие, приводящее к обмену между системой и окружающей средой веществом или энергией, то система перейдет в другое состояние равновесия, характеризующиеся другим набором параметров. Переход системы из одного состояния равновесия в другое называется термодинамическим процессом. В ходе процесса обязательно изменяется хотя бы один из параметров системы.

При постоянстве одного из термодинамических параметров процессы делятся наизотермический – при постоянной температуре (Т=const),изохорический(или изохорный) – при постоянном объеме (V=const),изобарический (или изобарный) – при постоянном давлении (р= const).

Процесс, при протекании которого система возвращается в исходное состояние, называется круговым или циклическим.

Химический процесс, являющийся, по сути, совокупностью химических реакций, протекает с изменением количеств веществ. Пусть система, состоящая из молекул вещества А, находится в состоянии термодинамического равновесия 1. При добавлении в эту систему молекул вещества В (воздействие на систему извне) она должна перейти в новое состояние равновесия. Одним из путей перехода является химическая реакция между молекулами А и В с образованием продуктов C и D:

n_аA + n_bB ® n_сC + n_dD.

Если между молекулами C и D протекает реакция с образованием молекул А и В: n_сC + n_dD ®n_аA + n_bB, то в состоянии равновесия 2 термодинамическая система будет состоять из смеси веществ A, B, C и D в соответствующих количествах. Химическая реакция запишется следующим образом:

n_аA + n_bB « n_сC + n_dD.

Если на данную систему было оказано воздействие извне (обмен энергией или веществом), то это приведет к переходу системы в состояние равновесия 3 с другим количеством веществ A, B, C и D. Причем, неочевидно, в каком направлении будет протекать химическая реакция, приводящая систему в состояние равновесия 3. Условились считать, что реакция протекает в прямом направлении, если количество исходных веществ (в нашем случае А и В) уменьшается, а количество продуктов реакции (в нашем случае C и D) увеличивается. Говорят, что реакция протекает в обратном направлении, если увеличивается количество исходных веществ при соответствующем уменьшении количества продуктов. Если реакция в системе может протекать в прямом и обратном направлении, то говорят, что она обратимая.

Очевидно, что для обратимых реакций «исходные реагенты и продукты реакции» – понятия условные и зависят от того, как записана реакция. При изменении записи химической реакции они меняются:

n_аA + n_bB « n_сC + n_dD,

n_сC + n_dD « n_аA + n_bB.

исходные « продукты

вещества реакции

Все процессы, встречающиеся в природе, бывают самопроизвольными и несамопроизвольными (вынужденными). Самопроизвольные процессы – это такие процессы, для протекания которых не требуются затраты энергии из окружающей среды. Примеры – переход теплоты от нагретого тела к холодному или процесс смешения газов. Несамопроизвольные процессы – это такие процессы, для протекания которых необходимы затраты энергии из окружающей среды. Пример – разделение газовых смесей.

По характеру перехода термодинамической системы из одного состояния равновесия в другое процессы делятся наравновесные (обратимые) и неравновесные (необратимые).

Равновесный (обратимый) процесс представляет собою бесконечную последовательность отдельных состояний равновесия. Система как бы все время находится в состоянии равновесия (квазистатический процесс). Его можно в любой момент заставить протекать в обратном направлении по тому же самому пути, изменив какой-либо параметр на бесконечно малую величину. Очевидно, что если время перехода системы в новое состояние равновесия (t) будет много меньше, чем время воздействия на систему (t) (t<< t), то можно считать, что в каждый момент времени система будет находиться в термодинамическом равновесии, что и является условием обратимости процесса. Такие процессы суть идеализация реальных процессов, экспериментально к ним можно только приблизиться, но никогда нельзя достигнуть. Если равновесный процесс провести сначала в прямом направлении, а затем в обратном, то система пройдет через те же состояния равновесия и не обнаружится никаких изменений как в самой системе, так и в окружающей среде. Работа, совершаемая системой в прямом процессе (W₁₂), будет равна работе, необходимой для возврата системы в исходное состояние (W₂₁). Работы прямого и обратного процесса равны по абсолютной величине и противоположны по знаку: W₁₂=–W₂₁ (условие термодинамической обратимости процесса).

В неравновесных (необратимых) процессах время перехода системы в состояние равновесия много больше, чем время воздействия на систему (t >> t). Поэтому в системе не устанавливается термодинамическое равновесие в промежуточных стадиях, и они не совпадают при прямых и обратных переходах. Работа, совершаемая системой в неравновесныхпроцессах при переходе из одного состояния равновесия в другое (W₁₂) не равна работе необходимой для возврата системы в исходное состояние (W₂₁). Если система совершала работу в прямом процессе, то для ее возврата в исходное состояние требуется бόльшая работа: W₁₂< W₂₁. Если в прямом процессе внешние силы совершали работу над системой, то при возвращении в исходное состояние термодинамическая система совершит меньшую работу: W₁₂>W₂₁.

Пример.Процесс изотермического расширения идеального газа.

Начальное (первое) состояние системы: идеальный газ при температуре Т находится под поршнем, нагруженным тремя гирями (рис.1.2), давление в системе р₁, занимаемый объем V₁. Конечное (второе) состояние системы: идеальный газ при температуре Т находится под разгруженным поршнем, давление в системе р₂, занимаемый объем V₂. Работа, совершаемая идеальным газом при переходе из первого состояния во второе, зависит от характера воздействия на систему. В случае бесконечно медленного снятия нагрузки с поршня (t<< t) система все время находится в состоянии равновесия, которое описывается уравнением Менделеева-Клапейрона. Элементарная работа, совершаемая системой, равна:

.

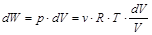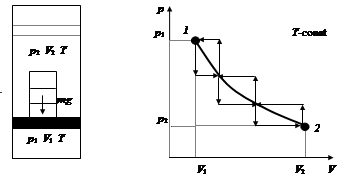Рис. 1.2. Процесс расширения (1-2) и сжатия (2-1) идеального газа

Тогда работа при переходе системы из состояния 1 в состояние 2, также как и из состояния 2 в состояние 1 , равна:

,

,

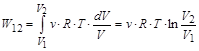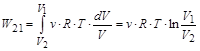W_равн =½W₁₂½ = ½W₂₁½.

Работа, совершаемая при переходе системы из одного состояния в другое, равна площади под кривой, описывающей этот переход, в координатах р-V (рис. 1.2).

В случае ступенчатого перехода системы из состояния 1 в состояние 2 (время разгрузки системы меньше, чем время установления равновесия в системе – t >> t) работа, совершаемая идеальным газом меньше, чем при реализации того же процесса в равновесных условиях (площадь под ломаной линией меньше): W₁₂ < W_равн. При проведении процесса в обратном направлении в этих же условиях W₂₁ > W_равн.

Внутренняя энергия

При анализе работы тепловой машины Джоуль (Joule), Гельмгольц (Helmholtz) и др. установили, что теплота, подводимая к системе из окружающей среды, расходуется на совершение механической работы и на изменение некоторого свойства системы, которое получило название внутренней энергии.

Внутренняя энергия (U) – это сумма всех видов энергии, которыми обладают отдельные частицы системы, за исключением кинетической и потенциальной энергии системы в целом и энергии, связанной с внешним электромагнитным и гравитационным полем.

Для систем, рассматриваемых в химической термодинамике, такими видами энергии могут быть кинетическая и потенциальная энергия атомов и молекул, энергия электронов в атомах, внутриядерная энергия и другие виды энергии. На сегодняшний день неизвестны и вряд ли когда-либо будут известны все виды энергии, заключенные в веществе, поскольку материя бесконечна и бесконечны формы ее движения. Но это не создает никаких проблем для практического использования понятия «внутренняя энергия». При расчете термодинамического процесса определяющим является не абсолютное значение величины внутренней энергии системы в начальном и конечном состояниях, а только ее изменение DU. Его можно определять, приняв за точку отсчета любое состояние термодинамической системы – так называемое стандартное состояние.

В химических процессах изменяются только две составляющие внутренней энергии:

1) химическая – энергия химических связей, включая энергию межмолекулярного взаимодействия. Изменение химической энергии происходит при протекании химической реакции в результате разрыва и образования химических связей в молекулах исходных веществ и продуктов реакции;

2) тепловая – кинетическая энергия движения атомов и молекул. Изменение тепловой энергии определяется изменением температуры системы как параметра кинетической энергии атомов и молекул.

Внутренняя энергия является функцией состояния системы, т.е. ее изменение в каком-либо процессе зависит только от начального и конечного состояний и не зависит от пути перехода.

Независимость изменения какого-нибудь свойства системы (X) от пути протекания процесса означает, что бесконечно малое приращение является полным дифференциалом (dX). Тогда элементарное количество внутренней энергии (бесконечно малое изменение) является полным дифференциалом (dU): 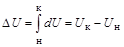. Если система совершает круговой процесс, то полное изменение внутренней энергии равно нулю: .

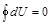Аналогичным свойством обладают и все остальные функции состояния системы. Величина DU (dU) считается положительной, если внутренняя энергия системы в ходе процесса увеличивается, и, соответственно, отрицательной, если уменьшается. Теплота (Q) и работа (W) в общем случае не являются функциями состояния, поскольку их изменение при переходе системы из одного состояния равновесия в другое зависит от пути протекания процесса. Соответственно элементарное количество (бесконечно малые изменения) теплоты (dQ) и работы (dW) в общем случае не являются полными дифференциалами. В равновесных процессах теплота и работа приобретают свойства функций состояния и их бесконечно малые изменения – свойства полных дифференциалов.

Единицей измерения внутренней энергии является [Дж], [кДж]. Внутренняя энергия термодинамической системы зависит от природы вещества, его количества (экстенсивная величина) и параметров состояния системы. Поэтому часто ее относят к одному молю (или килограмму) вещества, измеряя в [кДж/моль], [кДж/кг]. В литературе может встречаться внесистемная единица тепловой энергии – термохимическая калория (кал_тх): 1 кал_тх = 4,184 Дж.

Величину внутренней энергии системы, находящейся в состоянии равновесия, характеризует температура, поскольку она является параметром средней кинетической энергии молекул и атомов. Более высокой температурой обладают тела, у которых средняя кинетическая энергия молекул выше. Для идеального газа внутренняя энергия 1 моля газа зависит только от температуры.

Температура системы измеряется термометрами, действие которых основано на зависимости какого-либо физического свойства тела (объем, электрическое сопротивление и т.п.) от температуры с учетом принципа транзитивности теплового равновесия: если каждая из систем А и В находится в тепловом равновесии с системой С, то справедливо утверждение о тепловом равновесии А и В друг с другом. Все системы, находящиеся в тепловом равновесии друг с другом, будут обладать общим свойством – их температура будет одной и той же.

В термодинамике пользуются термодинамической шкалой температур. Абсолютная температура тела Т (температура по термодинамической шкале) всегда положительна. В системе СИ единицей измерения температуры является градус Кельвина (К).

Первое начало термодинамики

Джеймс Джоуль (Joule) в середине XIX века экспериментально обосновал закон сохранения энергии и определил механический эквивалент теплоты. На основании его работ этот закон был сформулирован в удобной для термодинамики форме и получил название"первое начало термодинамики": теплота (DQ), сообщенная термодинамической системе, идет на увеличение внутренней энергии (DU) системы и на совершение системой работы (DW).

Математическим выражением первого начала термодинамики является уравнение DQ =DU + DW. Для бесконечно малых изменений величин соответственно dQ = dU + dW.

Часто при протекании термодинамических процессов единственной работой системы является работа расширения, т. е. работа против внешнего давления (р): DW= р×DV. Тогда DQ =DU + р×DV , dQ = dU + р×dV.

Рассмотрим применение первого начала термодинамики к процессам, протекающим при постоянстве одного из параметров.

1. Изотермический процесс (Т=const). Энергия, подведенная к системе в виде теплоты, идет только на работу расширения системы: dQ_T = p×dV,DQ_T = p×DV.

2. Изохорный процесс (V=const, тогда DV=0). Система работы не совершает, поэтому все подведенное к системе тепло идет на увеличение ее внутренней энергии: dQ_V = dU,DQ_V =DU. Поскольку в данном случае DQ_V >0, так как система поглощает теплоту из окружающей среды, то и DU >0.

3. Изобарный процесс (p=const). Энергия, подведенная к системе в виде теплоты, идет на приращение внутренней энергии (DU >0) и на работу расширения системы (p×DV): dQ_р = dU + p×dV,DQ_р =DU + p×DV,

dQ_p = dU + p×dV = dU+ d(p×V) = d(U+ p×V).

Отметим, что в изотермичеческом, изохорном и изобарном процессах бесконечно малые изменения теплоты приобретают свойство полного дифференциала, т. е. теплота приобретает свойства функции состояния: U+ p×V может быть заменено функцией Н, H = U+ p×V, тогда, очевидно, dQ_p = dH.

Эта термодинамическая функция (H = U+ p×V) называется энтальпией (от греч. enthalpo — нагреваю).Она является функцией состояния системы и измеряется, как и внутренняя энергия, в [Дж], [кДж]. Она также зависит от количества вещества (экстенсивная величина), поэтому ее относят к одному молю (или килограмму) вещества [кДж/моль], [кДж/кг].

Физический смысл энтальпии явствует из ее определения (H = U+ p×V). Если взять какую-то систему, которая занимает объем V и находится под давлением p, то полная энергия этой системы будет суммой двух энергий: внутренней U и энергии, связанной с взаимодействием системы со средой (с энергией «стенки», отделяющей систему от окружающей среды), которая и обеспечивает давление p. Эта энергия будет пропорциональна p и будет тем больше, чем больше объем системы, т.е. пропорциональна V. Всю энергию системы можно, в принципе, превратить в тепло. Таким образом, система как бы содержит в себе определенное количество энергии, которую можно переводить в тепло. Таким образом энтальпия есть теплосодержание системы.

Энтальпию удобно использовать при рассмотрении энергетических эффектов в изобарных процессах. Поскольку изменение энтальпии характеризует количество теплоты, отданное или полученное системой, то оно соответствует тепловому эффекту реакции, протекающей при постоянном давлении.

Термохимические расчеты

Поскольку величины внутренней энергии, а следовательно, и энтальпии системы зависят от термодинамических параметров (температура, давление, количество вещества), то для термохимических расчетов необходимо привести тепловые эффекты реакций к одинаковым условиям. Чаще всего используют так называемые стандартные условия: давление p⁰ = 1,013×10⁵ Па , температура Т⁰ = 298,15 К. Этим условиям соответствуют стандартные тепловые эффекты химических реакций, которые обозначают D_rН⁰₂₉₈.

Иногда в целях упрощения записи, когда ясно, что речь идет о стандартных условиях, нижний индекс, указывающий температуру, опускают. Если температура отлична от стандартной, то нижний индекс показывает, к какой температуре относится тепловой эффект D_rН⁰_Т.

Наиболее удобными для экспериментального определения тепловых эффектов являются реакции образования сложных веществ из простых и реакции сгорания сложных веществ в кислороде. Значения стандартных тепловых эффектов этих реакций приведены в справочной литературе.

Энтальпия образования веществ. Условились, что стандартная энтальпия образования простых веществ, находящихся в устойчивом состоянии (наиболее устойчивая модификация), принимается равной нулю.

Пример.

1. Водород при стандартных условиях газ, энтальпия образования газообразного водорода D_fН⁰₂₉₈= 0 кДж/моль.

2. Ртуть при стандартных условиях жидкость, энтальпия образования жидкой ртути D_fН⁰₂₉₈= 0 кДж/моль.

3. Углерод при 298 К может существовать в нескольких модификациях, например в виде графита и алмаза. Так как графит устойчивее алмаза, то (D_fН⁰₂₉₈)_графит = 0 кДж/моль, а (D_fН⁰₂₉₈)_алмаз = 1,83 кДж/моль.

Тогда стандартнаяэнтальпия образования сложных веществ (теплота образования) является количеством теплоты, которое поглощается или выделяется при образовании в стандартных условиях одного моля сложного вещества из простых веществ, взятых в наиболее устойчивой модификации:

1/2 А₂ + 1/2 В₂ = АВ + D_fН⁰₂₉₈.

Стандартная энтальпия образования веществ обозначается D_fН⁰₂₉₈ [кДж/моль]; индекс f происходит от англ. formation – образование. Известные значения стандартных энтальпий образования веществ приведены в справочной литературе, в разделе термодинамические характеристики веществ.

Теплота сгорания – это количество теплоты, которое выделяется при полном сгорании одного моля вещества при стандартных условиях. Полным сгоранием является реакция взаимодействия исходного вещества и кислорода с образованием продуктов окисления атомов, входящих в молекулу вещества. Принято считать, что продуктами окисления углерода, водорода, азота, галогенов (Hal), металлов (Ме) будут являться соответственно CO₂, H₂O (жидкость), N₂, HHal, Me_xO_y.

Пример.Реакция полного сгорания вещества C_cH_hN_nO_oF_f имеет вид

C_cH_hN_nO_oF_f + x O₂ = c CO₂ + ( 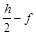) H₂O + 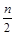N₂ + f HF.

Стандартная энтальпия сгорания веществ обозначается D_сН⁰₂₉₈, [кДж/моль]; индекс с происходит от английского combustion – сгорание.

Следствия из закона Гесса. Теплоты образования и сгорания веществ широко используют при определении тепловых эффектов химических реакций. Расчеты проводят на основании следствий из закона Гесса.

Первое следствие: тепловой эффект реакции равен разности между суммой энтальпий образования продуктов реакции и суммой энтальпий образования исходных веществ с учетом числа молей реагирующих веществ:

D_rН⁰₂₉₈=(ån_iD_fН⁰_i)_{продукты}–(ån_iD_fН⁰_i)_{исх. вещества}.

Для реакции n_аA + n_bB = n_сC + n_dD тепловой эффект рассчитывается по уравнению

D_rН⁰₂₉₈=(n_c×D_fН⁰_C + n_d×D_fН⁰_D )–(n_a×D_fН⁰_A + n_b×D_fН⁰_B ).

Второе следствие: тепловой эффект реакции равен разности между суммой теплот сгорания исходных веществ и суммой теплот сгорания продуктов реакции с учетом числа молей реагирующих веществ: D_rН⁰₂₉₈=(å n_i×D_cН⁰_i) _{исх. вещества} –(å n_i×D_cН⁰_i ) _{продукты} .

Для реакции n_аA + n_bB = n_сC + n_dD тепловой эффект рассчитывается по уравнению

D_rН⁰₂₉₈=(n_a×D_сН⁰_A + n_b×D_сН⁰_B)–(n_c×D_сН⁰_C + n_d×D_сН⁰_D).

Примеры.

1. Определение стандартного теплового эффекта реакции, если известны теплоты образования веществ.

Реакция образования сульфата алюминия из оксида алюминия и триоксида серы:

Al₂O_{3 (кр)} + 3SO_{3 ( газ)} = Al₂(SO₄)_{3 (кр)}

D_fН⁰₂₉₈, кДж/моль –1676,1 –395,9 –3442,8.

Решение.Тепловой эффект реакции определяем по первому следствию из закона Гесса:

D_rН⁰₂₉₈=(å n_i×D_fН⁰_i) _{продукты}–(å n_i×D_fН⁰_i )_{исх. вещества}

в соответствии с уравнением реакции

D_rН⁰₂₉₈ = 1×(–3442,8) – [–1676,1 + 3×(–395,9)] = –579 [кДж].

Реакция взаимодействия метана и диоксида углерода с образованием оксида углерода и водорода:

CH_{4 (газ)} + CO_{2 (газ)} = 2 CO _(газ) + 2H_{2 (газ)}

D_fН⁰₂₉₈, кДж/моль –74,85 –393,51 –110,5 0

Решение.Тепловой эффект реакции определяем по первому следствию из закона Гесса:

D_rН⁰₂₉₈=(å n_i×D_fН⁰_i) _{продукты}–(å n_i×D_fН⁰_i )_{исх. вещества}

в соответствии с уравнением реакции

D_rН⁰₂₉₈ =[2×(–110,5) + 2×0] – [(–74,85) + (–393,51)] = 247,36 [кДж].

2. Определение стандартного теплового эффекта реакции, если известны стандартные теплоты сгорания веществ.

Реакция взаимодействия уксусной кислоты и этилового спирта с образованием сложного эфира – этилацетата:

CH₃COOH_(ж) + C₂H₅OH_(ж) = CH₃COOC₂H_5(ж) + H₂0_(ж)

D_cН⁰₂₉₈, кДж/моль –873,79 –1366,91 –2254,21 0

Решение.Тепловой эффект реакции определяем по второму следствию из закона Гесса:

D_rН⁰₂₉₈=(å n_i×D_cН⁰_i) _{исх. вещества} –(å n_i×D_cН⁰_i ) _{продукты}

в соответствии с уравнением реакции

D_rН⁰₂₉₈ = [1×(–873,79) +1×(–1366,91)] – [1×(–2254,21)] = 13,51[кДж].

Второе начало термодинамики

Анализ работы идеальной тепловой машины по циклу Карно, показал, что коэффициент полезного действия h, не зависит от природы рабочего тела, а определяется только температурным интервалом, в котором совершается работа (теорема Карно-Клаузиуса) (Carnot; Clausius):

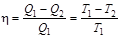или ,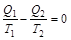

где Q₁ – количество теплоты, сообщенное рабочему телу при температуре T₁; Q₂ – количество теплоты, отданное рабочим телом при температуре T₂.

Если представить цикл Карно суммой бесконечно малых циклов, в каждом из которых 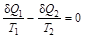, то в циклическом процессе 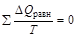, а это значит, что интеграл, взятый по замкнутому контуру, равен нулю: 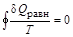. Следовательно, подынтегральная функция 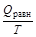является функцией состояния. Эту функцию Клаузиус назвал энтропией (S) (entropia — превращение).

Для обратимого (равновесного) процесса изменение энтропии равно:

, .

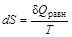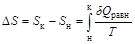Для необратимого (неравновесного) процесса, как было показано на примере расширения идеального газа, работа, производимая системой в самопроизвольном процессе, меньше работы, производимой в равновесном процессе: W_неравн< W_равн. Принимая во внимание первое начало термодинамики dU =dQ + dW и учитывая, что внутренняя энергия – функция состояния (dU_равн=dU_неравн), получаем, что dQ_неравн >dQ_равн. Соответственно для необратимого (неравновесного) процесса изменение энтропии .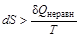

В общем случае для любого процесса можно написать:

, ;

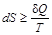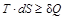знак равенства относится к равновесным процессам, знак неравенства – к неравновесным.

Согласно первому началу термодинамики dQ = dU + p×dV, следовательно, T×dS ³ dU + p×dV. В изолированной системе dU = dV =0, а так как Т >0, то dS ³0.

Второе начало термодинамики утверждает, что в изолированной системе самопроизвольно протекают процессы с увеличением энтропии, которые прекращаются при достижении ее максимального значения, соответствующего состоянию термодин