Второе и третье начала термодинамики

Второе начало термодинамики: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает (закон возрастания энтропии).

Если первое начало термодинамики выражает закон сохранения и превращения энергии применительно к термодинамическим процессам безотносительно их направления, то второе начало термодинамики определяет направление протекания термодинамических процессов, указывая, какие процессы в природе возможны, а какие - нет.

Существуют ещё две формулировки второго начала термодинамики:

1) по Кельвину:невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;

2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к телу более нагретому.

Третье начало термодинамики - теорема Нернста-Планка - постулирует поведение термодинамических систем при нуле Кельвина: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:

.

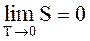Тепловые двигатели и холодильные машины

Тепловой двигатель - это периодически действующий двигатель, совершающий работу за счет полученной извне теплоты.

Термостатом называется термодинамическая система, которая может обмениваться теплотой с телами практически без изменения собственной температуры.

Рабочее тело - это тело (газ или пар), совершающее круговой процесс и обменивающееся энергией с другими телами.

Принцип работы теплового двигателя: от термостата с более высокой температурой 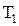, называемого нагревателем, за цикл отнимается количе­ство теплоты 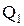, а термостату с более низкой температурой 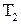, называемому холодильником, за цикл передается количество теплоты 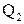. При этом рабочее тело расширяется и совершает работу 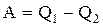(рис.18).

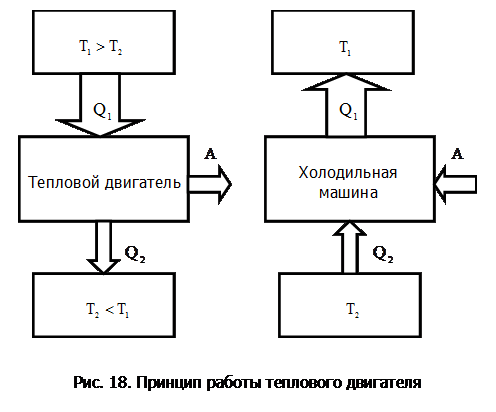
Термический КПД двигателя:

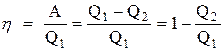
Чтобы КПД был равен 1, необходимо, чтобы 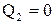, а это запрещено

вторым началом термодинамики.

Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине: от термостата с более низкой температурой 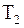за цикл отнимается количество теплоты 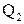и отдается термостату с более высокой температурой 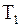. При этом 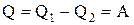или .

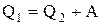Количество теплоты 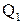, отданное системой термостату 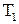, больше количества теплоты 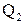, полученного от термостата 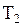, на величину работы, совершенной над системой.

Эффективность холодильной машины характеризует холодильный коэффициент 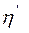- отношение отнятой от термостата с более низкой температурой количества теплоты 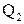к работе 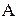, которая затрачивается на приведение холодильной машины в действие:

.

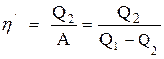Теорема Карно

Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей и холодильников , наибольшим КПД обладают обратимые машины. При этом КПД обратимых машин, равны друг другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника.

Для построения рабочего цикла использует обратимые процессы. Например, цикл Карно состоит из двух изотерм (1–2, 2-4), в которых теплота полностью превращается в работу, и двух адиабат (2-3, 4–1), в которых изменение внутренней энергии полностью превращаются в работу (рис. 19).

Рассмотрим изменение энтропии рабочего тела. Общее изменение энтропии в цикле:

Так как мы рассматриваем только обратимые процессы, общее изменение энтропии .

Последовательные термодинамические процессы в цикле Карно:

Процесс	Работа	Изменение энтропии	Наблюдается
Изотермическое расширение 1—2			тело принимает теплоту
Адиабатическое расширение 2—3 ;			охлаждение до
изотермическое сжатие 3-4			тело отдает теплоту
адиабатическое сжатие ;			восстановление начального состояния

Общее изменение энтропии в равновесном цикле: , поэтому: -максимальный КПД теплового двигателя.

Следствия:

1. КПД цикла Карно не зависит от рода рабочего тела.

2. КПД определяется только разницей температур нагревателя и холодильника.

3. КПД не может быть 100% даже у идеальной тепловой машины, так как при этом температура холодильника должна быть , что запрещено законами квантовой механики и третьим законом термодинамики.

4. Невозможно создать вечный двигатель второго рода, работающий в тепловом равновесии без перепада температур, т.е. при , так как в этом случае .

Тепловые двигатели повышают энтропию замкнутой системы.

РЕАЛЬНЫЕ ГАЗЫ

Уравнение Ван-дер-Ваальса

Как показывают эксперименты, модель идеального газа позволяет описывать поведение разреженных реальных газов лишь при «нормальных» условиях, т.е. при достаточно низком давлении и высокой температуре. При высоких давлениях, или низких температурах уравнение состояния дает большие расхождения с результатами экспериментов.

При выводе уравнения состояния идеального газа не учитывались размеры молекул и потенциальная энергия их взаимодействия. Поэтому физическая природа газа не играла никакой роли и уравнение состояния универсально и применимо ко всем газам. Повышение давления приводит к уменьшению среднего расстояния между молекулами, значит, необходимо учитывать объем молекул и взаимодействие между ними.

Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, Ван-дер-Ваальс вывел уравнение состояния реального газа, введя в уравнение Клапейрона-Менделеева две поправки.

1. Учет собственного объема молекул.

Для движения молекул предоставлен не весь объем , занимаемый газом, а меньший на величину объема всех молекул газа ‑ , где ‑ суммарный объем молекул газа, - молярный объем. Расчеты показывают, что константа численно равна учетверенному объему молекул, содержащихся в моле газа. Размерность поправки .

2.Учет притяжения молекул.

Действие сил притяжения молекул газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. Внутреннее давление равно

,

где – постоянная Ван-дер-Ваальса, характеризующая силы притяжения молекул. Размерность коэффициента: .

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):

(23)

Для произвольного количества вещества газа с учетом того, что , уравнение (23) имеет вид:

где поправки и - постоянные для каждого газа величины, определяемые опытным путем.