Описывает ориентацию орбиталей в пространстве.

Может принимать целочисленные значения в диапазоне от -l до +l (включая 0). Например:

Для l=0 возможно только одно значение: m=0. Это значит, что s-орбиталь имеет только одну пространственную ориентацию.
Для l=1: m=-1;0;+1 - p-орбиталь имеет три пространственные ориентации.
Для l=2: m=-2;-1;0;+1;+2 - d-орбиталь имеет пять пространственных ориентаций.

Спиновое квантовое число m_s

Описывает направление вращения электрона в магнитном поле - по часовой стрелке или против. На каждой орбитали может находиться только два электрона: один со спином +½ другой -½.

Квантовые числа для первых трех энергетических уровней:

n	l	Орбиталь	m	ms
		1s		+½ -½
		2s		+½ -½
		2p	-1 0 +1	+½ -½ +½ -½ +½ -½
		3s		+½ -½
		3p	-1 0 +1	+½ -½ +½ -½ +½ -½
		3d	-2 -1 0 +1 +2	+½ -½ +½ -½ +½ -½ +½ -½ +½ -½

На первом уровне (n=1) есть только s-орбиталь, на которой может находиться только 2 электрона со спинами +1/2 и -1/2. Это справедливо для s-орбитали любого уровня: 1s; 2s; 3s…

На втором энергетическом уровне (n=2) есть уже две орбитали s; p. На третьем (n=3) - три орбитали: s, p, d. и т.д. С каждым новым энергетическим уровнем добавляется новая орбиталь.

Для 2p-орбитали существует три пространственных ориентации (формы облака), на каждой из которых может находиться по два электрона. Т.е. на втором энергетическом может находиться не более 6 p-электронов.

Для 3d - максимум 10 d-электронов и пять форм облаков.

Главные энергетические уровни отличаются энергией. Чем выше уровень - тем выше энергия. С другой стороны, различные орбитали одного и того же уровня также обладают разной энергией:
Энергия электронов на орбитали 2p выше, чем на 2s
Энергия электронов на орбитали 3p выше, чем на 3s
Энергия электронов на орбитали 3d выше, чем на 3s
Энергия электронов на орбитали 3d выше, чем на 3p

Что же касается электронов "внутри орбиталей", то их энергии одинаковы (так у всех десяти электронов 3d-орбитали энергии одинаковы).

Постулат Де-Бройля

Волнова́я фу́нкция, или пси-фу́нкция — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

где — координатный базисный вектор, а — волновая функция вкоординатном представлении.

Согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точкеконфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

Уравнение Шредингера — основное уравнение нерелятивистской квантовой механики, описывающее динамику частиц. Предложено Э. Шредингером в 1926 г. Состояние классической частицы в любой момент времени описывается заданием ее координат и импульсов (x,y,z,p_x,p_y,p_z). Зная эти величины в момент времени t, можно определить эволюцию системы под действием известных сил во все последующие моменты времени. Координаты и импульсы частиц сами являются величинами, непосредственно измеряемыми на опыте. В кван­то­вой физике состояние системы описывается волновой функцией ψ(x,y,z,t). Т. к. для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса, то не имеет смысла говорить о движении частицы по определенной траектории, можно определить только вероятность нахождения частицы в данной точке в данный момент времени, которая определяется квадратом модуля волновой функции

W ~ |ψ(x,y,z,t)|².

Эволюция квантовой системы в нерелятивистском случае описывается волновой функцией, удовлетворяющей уравнению Шредингера

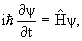
где ψ(x,y,z,t) − волновая функция, 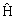− оператор Гамильтона (оператор полной энергии системы).