Идеальный газ. Основное уравнение молекулярно – кинетической теории газов. Постоянная Больцмана. Температура и давление как статистические величины.

Одной из особенностей физики является использование абстракций и модельных процессов, которые позволяют при изучении некоторых явлений не учитывать не очень существенные их стороны. Простейшей моделью молекулярно-кинетической теории является модель идеального газа.

В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений (т.е. силы межмолекулярного взаимодействия отсутствуют). Время соударения молекул значительно меньше времени между соударениями. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ (т.е. молекулы рассматриваются как материальные точки).

Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Опыт показывает, что при давлениях, близких к атмосферному, и температурах, близких к комнатной, многие газы (азот, кислород, водород, пары воды и т.д.) можно считать идеальными. Энергией взаимодействия молекул между собой здесь можно пренебречь потому, что в этих условиях лишь небольшая доля молекул находится в каждый момент времени в состоянии соударения.

В результате каждого столкновения между молекулами и молекул со стенкой скорости молекул могут изменяться по модулю и по направлению; на интервалах между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т.е. подчиняются законам механики Ньютона.

Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление газа, его температура).

Свойство газа оказывать давление на стенки сосуда, в котором он находится – одно из основных его свойств. Именно своим давлением газ и обнаруживает свое присутствие. Поэтому величина давления является одной из главных характеристик газа.

По определению давление газа

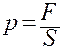: (1)

где F – сила, которая действует со стороны молекул газа на площадку S стенки сосуда с газом.

Используя модель идеального газа, вычислим давление газа на стенку сосуда. Пусть в сосуде с расстоянием l между стенками 1 и 2 находится N молекул. Рассмотрим движение одной молекулы массой m. Столкновение молекулы со стенкой абсолютно упругое, т.е. скорость молекулы не изменяется по модулю после столкновения. В процессе упругого взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υ_x скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, не изменяясь по модулю(υ_1x = υ_2x = υ_x), а проекция υ_y скорости, параллельная стенке, остается неизменной (рис.1.).

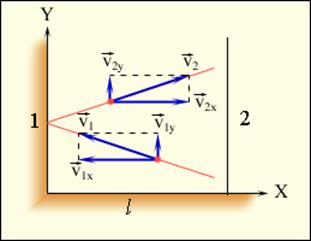
Рис.1.Упругое столкновение молекулы со стенкой.

Определим нормальную составляющую импульса (вдоль оси X), которую получает стенка при ударе молекулы, т.е. изменение импульса молекулы.

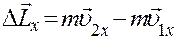(2)

В проекции на ось X, с учетом того, что проекция скорости молекулы на ось X не изменяется по модулю из (2) получим:

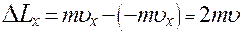(3)

Касательная к стенке составляющая (вдоль оси Y) не влияет на величину давления. В среднем ее величина будет равна нулю.

После столкновения со стенкой 1 молекула движется к стенке 2, соударяется с ней и опять ударяется о стенку 1. Очевидно, что число ударов Z этой молекулы о стенку 1 за время Δt будет равно:

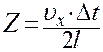, (4)

где 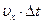- путь, пройденный молекулой вдоль оси X за время Δt.

Тогда за время Δt молекула передаст стенке 1 импульс

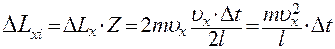(5)

Согласно II закону Ньютона импульс, который молекула передает стенке 1 за время Δt (изменение импульса стенки) равен импульсу силы, действующей на стенку за тоже время. Запишем II закон Ньютона для i-ой молекулы

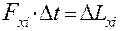(6)

С учетом (5) перепишем (6) в виде

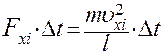
Отсюда

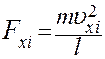(7)

Сила, которая действует на стенку 1 вдоль оси X, со стороны всех N молекул равна

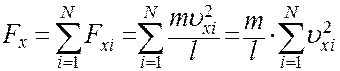(8)

Умножим и разделим правую часть (8) на число молекул N

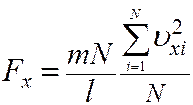(9)

Величина

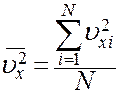(10)

это среднее значение квадрата скорости молекулы вдоль оси X (не путать с квадратом средней скорости 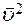). С учетом (10) перепишем (9) в виде

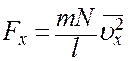(11)

Из (1) с учетом (11) определим величину давления газа на стенку

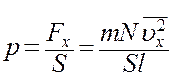(12)

где S – площадь стенки. Следует учесть, что Sl = V – объем сосуда. С учетом этого из (12) получим

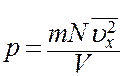(13)

В (13) N/V = n – число молекул в единице объема, т.е. концентрация молекул. С учетом этого перепишем (13) в виде

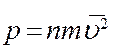(14)

Скорость i – ой молекулы можно определить, зная ее проекции на оси координат

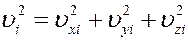
Усредним это уравнение по всем молекулам

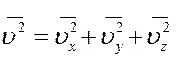(15)

Очевидно, что все направления движения молекул в сосуде равновероятны из–за полной хаотичности движения молекул. Следовательно, средние значения квадратов проекций скоростей на оси координат равны.

.

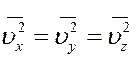С учетом этого из (15) получим

.

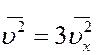Из последнего уравнения получим

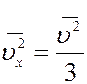(16)

Подставим (16) в (14)

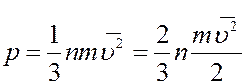(17)

где 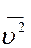- среднее значение квадрата скорости. Величина 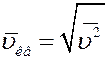называется средней квадратичной скоростью молекул.

В (17) величина

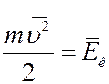
есть не что иное, как средняя кинетическая энергия одной молекулы газа. С учетом этого (17) примет вид

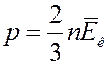(18)

(18) – уравнение Клаузиуса. Из (18) следует: давление газа равно двум третям средней кинетической энергии поступательного движения молекул, которые содержатся в единице объема газа.

Это один из важнейших выводов кинетической теории идеального газа. Уравнения (17) и (18) устанавливают связь между микроскопическими величинами, т.е. величинами, относящимися к отдельной молекуле и величиной давления – макроскопической величине, характеризующей газ как целое, которую можно измерить непосредственно.

(17) и (18) – основное уравнение кинетической теории газов.

Уравнению (17) можно придать другой вид. Известно:

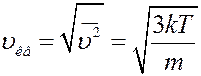, (19)

где m – масса молекулы, T – температура газа. С учетом (19) из (17) получим

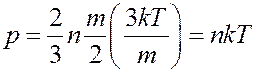. (20)

Из (18) и (20) следует:

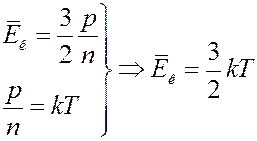. (21)

(21) – уравнение Больцмана. Следует обратить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не зависит от ее массы, а является только функцией температуры. Броуновская частица, взвешенная в жидкости или газе, обладает такой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частицы. Этот вывод распространяется и на случай, когда в сосуде находится смесь химически невзаимодействующих газов, молекулы которых имеют разные массы. В состоянии равновесия молекулы разных газов будут иметь одинаковые средние кинетические энергии теплового движения, определяемые только температурой смеси.

Коэффициент k в (21), выражающий соотношение между единицей энергии и единицей температуры называется постоянной Больцмана. Постоянная Больцмана одна из фундаментальных физических констант. Постоянная Больцмана дает возможность напрямую связать характеристики микромира с характеристиками макромира — в частности, с показаниями термометра. Уравнение (21) прокладывает мостик между двумя мирами, связывая характеристики атомного уровня (в левой части) с объемными свойствами (в правой части), которые можно измерить при помощи человеческих приборов, в данном случае термометров. Очевидно, что численное значение постоянной Больцмана должно быть установлено экспериментально. Ввиду важности этой постоянной она была определена многими методами. В системе единиц СИ:

.

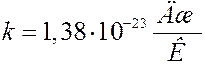Из уравнения Больцмана вытекает, что средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.

Следовательно, температура есть мера средней кинетической энергии поступательного движения молекул.

Из (21) следует, что абсолютный нуль температуры это температура, при которой средняя кинетическая энергия хаотического движения молекул равна нулю, т.е. температура, при которой хаотические движения молекул прекращаются. Это и есть тот абсолютный нуль, начало отсчета абсолютной температуры. Из этого же уравнения вытекает, что отрицательной абсолютной температуры быть не может, так как кинетическая энергия положительная величина.

В соответствии с МКТ давление газа обусловлено столкновениями молекул со стенками сосуда. Так как движение молекул полностью хаотично, то в отдельные моменты времени число молекул, которые сталкиваются со стенкой и их скорости могут отличаться от средних значений этих величин в ту или другую сторону. Поэтому будут наблюдаться флуктуации давления около некоторого среднего значения. Если общее число молекул невелико, то флуктуации давления могут быть сравнимы с величиной самого давления. В случае одной или малого числа молекул теряется смысл понятия давления газа, также как и понятие его плотности.

Отсюда следует, что давление газа это величина, связанная с тем, что газ состоит из большого числа молекул. О таких величинах, которые имеют смысл только для систем состоящих из очень большого числа частиц, говорят, что они имеют статистический характер. Таким образом, давление газа – статистическая величина.

Поскольку температура определяется средней энергией хаотического движения молекул, она, как и давление, является статистической величиной. Поэтому нельзя говорить о “температуре” одной или нескольких молекул, о “горячих” или ”холодных” молекулах. Не имеет смысла говорить о температуре газа в космическом пространстве, где число молекул в единице объема настолько мало, что они не образуют газ в обычном смысле слова. Следовательно, нельзя говорить об их средней кинетической энергии.

Лекция 4