Активность растворов электролитов

Теория Аррениуса, базирующаяся на представлениях о полной диссоциации молекул в растворе, дает правильное количественной описание свойств разбавленных растворов, для которых основную роль играет число частиц растворенного вещества в единице объема раствора. При этом не учитываются различия в силах взаимодействия между заряженными и незаряженными частицами, принимая все силы межчастичных взаимодействий силами Ван-дер-Ваальса. Такой подход вполне оправдан, когда речь идет о разбавленных слабых электролитах.

Однако для растворов сильных электролитов, даже разбавленных, большую роль играют дальнодействующие электростатические силы, которые достаточно медленно убывают с расстоянием.

По современным представлениям, ионы в растворе окружены определенным числом ориентированных диполей растворителя, которые прочно удерживаются вблизи иона и участвуют в тепловом движении вместе с ним как единое целое. Этот «комплекс», образующийся в результате первичной сольватации (первичная сольватная оболочка), в результате вторичной сольватации окружен вторым слоем молекул растворителя (вторичная сольватная оболочка), не столь правильно ориентированных и совершающих самостоятельные тепловые движения. Вокруг каждого иона в растворе находится сольватная оболочка, которая препятствует их соединению в не диссоциированные молекулы.

Теплоты сольватации солей велики и соизмеримы с тепловыми эффектами обычных химических реакций. Высокая теплота сольватации показывает, что ионы образуют очень прочные сольваты, характеризующиеся малым значением внутренней энергии. Теплота сольватации тем больше, чем выше заряд иона и чем меньше его радиус. Сольватация ионов приводит к существенным нарушениям молекулярной структуры растворителя, что имеет особенное значение для водных растворов. При рассмотрении водных растворов электролитов для сольватации используют специальный термин - гидратация.

В растворах электролитов рассчитанная концентрация ионов в растворах не совпадает с экспериментальными значениями из-за взаимодействия ионов растворенного вещества между собой. В связи с этим Льюисом [8] было введено понятия об активности и коэффициенте активности. Поэтому для применения к реальным системам, описывающих свойства идеальных растворов, вместо обычных величин - давления, концентрации - в них стали использовать величины, взятые из опыта. Так, давление пара заменялась на величину, названную летучестью, или фугитивностью, а концентрация - на активность.

Если, например, формулу кислоты представить в общем виде как HA, то уравнение

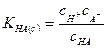(32.10)

определяющее константу диссоциации слабой кислоты и справедливое для идеальных систем и выраженную через концентрации ионов, то по Льюису применительно к реальным системам имеет вид

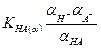(32.11)

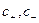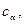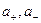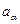Уравнение (32.11) совпадает по форме с уравнением (32.10) и правильно описывает поведение реального раствора. Это достигается тем, что в него входят не концентрации ионов и недиссоциированного электролита а соответствующие активности и . Значения активностей выбираются так, чтобы величина константы диссоциации оставалась одной и той же независимо от общей концентрации электролита. Термодинамическая константа диссоциации 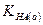, в отличие от концентрационной константы диссоциации 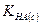, определяемой из уравнения (32.10), будет постоянной величиной для данного электролита при определенной температуре.

Существует три способа выражения активностей для выражения концентрации растворов: c - молярная, m - моляльная и X - мольная доля (рациональная шкала).

Активность в отличие от концентрации учитывает силы взаимодействия между частицами, проявляющиеся в реальных растворах. Поэтому активность можно представить как произведение концентрации на некоторый переменный фактор, называемый коэффициентом активности и включающий поправку на силы взаимодействия:

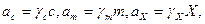(32.12)

где 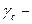молярный; 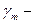моляльный; 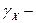рациональный коэффициенты активности.

Физический смысл коэффициента активности становится понятным на

основании рассмотрения двух растворов одного и того же вещества в одинаковом растворителе, которые находятся в идеальном (сильно разбавленный раствор) и неидеальном (концентрированный раствор) состояниях. Из основных термодинамических понятий и соотношений вытекает нижеследующее.

Химический потенциал растворенного вещества 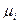в идеальном растворе отвечает выражению

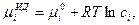(32.13)

а в неидеальном –

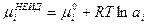(32.14)

Учитывая (32.12) и вычитая из уравнения (32.14) уравнение (32.13), получим:

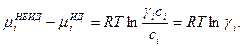(32.15)

Исходя из того, что химическим потенциалом i-го компонента термодинамической системы в данной фазе называется частная производная термодинамического потенциала (чаще свободной энергии Гиббса 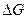) по числу молей 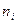этого компонента при неизменном числе молей остальных компонентов и неизменности соответствующих параметров состояния, выражение (32.15) может быть преобразовано с учетом того, что 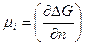следующим образом:

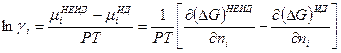. (32.16)

При этом известно, что система в идеальном состоянии не совершает полезной работы, т. е. 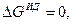а работа, совершаемая системой в неидеальном состоянии, равна убыли термодинамического потенциала, т. е. .

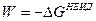Таким образом, для каждого моля i -го компонента

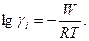(32.17)

Уравнение (32.17) показывает, как коэффициент активности связан с той максимальной работой, которую нужно совершить, чтобы перенести 1 моль вещества из неидеального раствора в идеальный.

Определить активность отдельного сорта ионов, а, следовательно, и их коэффициент активности из опытных данных невозможно, так как уравнения, которые можно было бы использовать для нахождения активностей, содержат не активность какого-либо одного сорта ионов, а произведение активностей всех ионов данного электролита. Поэтому введено понятие средней активности, как среднее геометрическое из активностей ионов, составляющих данный электролит. Для электролита, распадающегося на v положительных ионов и v отрицательных ионов, средняя активность будет

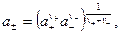(32.18)

а для бинарного электролита –

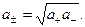
Аналогично можно определить и средний коэффициент активности электролита, распадающегося на 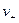и 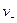ионов,

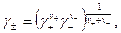(32.19)

и соответственно для бинарного электролита

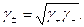(32.20)

В разбавленных растворах сильных электролитов средний[3] коэффициент активности электролита зависит только от ионной силы раствора (понятие введено Льюисом и Рендаллом) и не зависит от природы ионов, находящихся в растворе (одна из формулировок закона ионной силы). Поэтому его можно определить и по ионной силе раствора.

Ионная сила I разбавленного раствора сильного электролита (или смеси электролитов) равна полусумме произведений концентраций ионов на квадраты их зарядов, т. е.

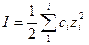и 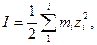(32.21)

где 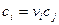и 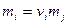- молярная и моляльная концентрация 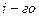иона, соответственно; 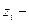заряд i-ого иона; 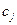и 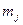- молярность и моляльность j-го электролита; 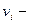число i-ых ионов, на которые распадается j-тый электролит.

Для разбавленного раствора одного электролита с концентрацией c или т выражения (32.21) примут вид

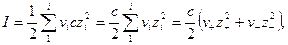
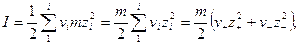(32.22)

Для раствора 1-1 - электролита ионная сила равна концентрации, т. е I=c или I=m, а для других электролитов она всегда больше концентрации. Например, для 2-2 - сильного электролита с молярностью c (при допущении, что 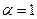и 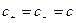) ионная сила равна учетверенной концентрации

.

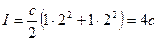Экспериментально установленная зависимость ионной силы и коэффициента активности формулируется в виде закона ионной силы: в растворах с оди­наковой ионной силой коэффициенты активности одинаковы. Другими слова­ми, для разбавленных растворов различных электролитов в одинаковом растворителе при 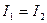имеем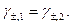

Это положение может быть объяснено на основе электростатической теории растворов электролитов - теории Дебая и Гюккеля.