Колебательно-вращательные спектры многоатомных молекул.
Трехатомная молекула не может быть описана моделью гармонического осциллятора, так как обладает ни одной, а несколькими степенями свободы. Поэтому колебательно-вращательный спектр многоатомных молекул содержит целый набор линий, интенсивности и частоты которых отражают особенность сложного колебательного движения в молекулах.
Если молекула состоит из N атомов, то в пространстве трех измерений у нее будет (3N-6) степеней свободы. Если молекула линейная, то число степеней свободы (3N-5).
Так как колебания отдельных атомов связаны друг с другом, то колебательное движение можно представить как суперпозицию колебаний набора свободных осцилляторов. Удобно выбрать естественную систему координат, которая задается расположением атомов в молекуле и характеризуется значением длин связей и углов между связями.
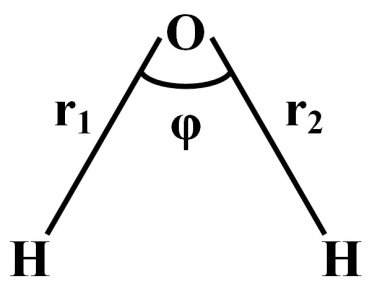
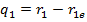 ,
, 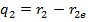 ,
, 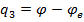
Общее число естественных координат равно числу степеней свободы.
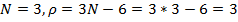
Нужно выразить полную энергию молекулы через координаты:
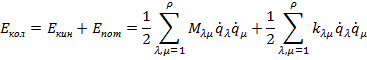
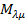 – приведенная масса,
– приведенная масса, 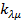 – постоянная упругой связи между атомами с координатами
– постоянная упругой связи между атомами с координатами 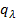 и
и 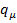 .
.
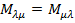 и
и 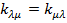
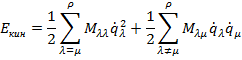
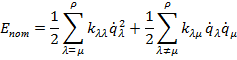
В этих выражениях первые слагаемые характеризуют взаимодействие атомов, связанных химической связью и имеющих общую координату 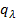 . Второе слагаемое в первой сумме характеризует взаимодействие различных естественных координат или динамическое взаимодействие. Оно не зависит от квазиупругих сил и связано с характером движения колебания частиц. Второе слагаемое во второй сумме характеризует взаимодействие естественных координат, определяемое квазиупругими силами и выражается через силовые постоянные k. Если различные связи в молекуле независимы, вторые слагаемые будут равны нулю. Количество энергии такой системы можно представить как:
. Второе слагаемое в первой сумме характеризует взаимодействие различных естественных координат или динамическое взаимодействие. Оно не зависит от квазиупругих сил и связано с характером движения колебания частиц. Второе слагаемое во второй сумме характеризует взаимодействие естественных координат, определяемое квазиупругими силами и выражается через силовые постоянные k. Если различные связи в молекуле независимы, вторые слагаемые будут равны нулю. Количество энергии такой системы можно представить как:
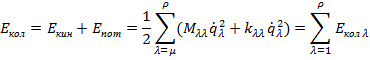
Каждый гармонический осциллятор будет колебаться как:
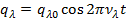
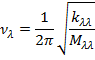
Для того чтобы многоатомную молекулу можно было рассматривать как совокупность ρ невзаимодействующих гармонических осцилляторов, нужно перейти от исходных естественных координат к их линейным комбинациям:
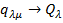
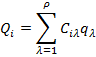
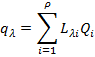
Новые координаты называются нормальными, их число тоже равно числу степеней свободы, они связаны с естественными координатами через коэффициенты преобразования С и λ или нормированные коэффициенты формы колебаний 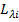 . С помощью нормальных координат удается выразить полную колебательную энергию молекулы как сумму отдельных энергий осцилляторов.
. С помощью нормальных координат удается выразить полную колебательную энергию молекулы как сумму отдельных энергий осцилляторов.
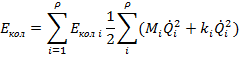
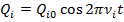
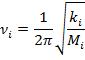
Основное свойство нормальных колебаний: при таком колебании с частотой 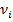 колеблются все без исключения атомы молекулы, и фаза колебаний всех атомов оказывается одинаковой. Поэтому в колебательных спектрах многоатомных молекул проявляются частоты нормальных колебаний.
колеблются все без исключения атомы молекулы, и фаза колебаний всех атомов оказывается одинаковой. Поэтому в колебательных спектрах многоатомных молекул проявляются частоты нормальных колебаний.
Второе свойство: при равенстве частот и фаз колебаний всех частиц, образующих молекулу, амплитуды и направления движения могут сильное отличаться.
Соотношение всех амплитуд, с которыми при данном нормальном колебании изменяются естественные колебательные координаты, называется формой нормального колебания. Форма нормального колебания определяется совокупностью коэффициентов преобразования С и λ, характеризующих вклад в данное нормальное колебание различных естественных координат.
Для того чтобы рассчитать колебательный спектр молекулы, нужно решить две задачи:
- механическая (1 этап: составляются уравнения движения системы, имеющие степень, равную числу степеней свободы - вековое уравнение; 2 этап: решают вековое уравнение, находят частоты и формы нормальных колебаний).
- электрооптическая (определяют интенсивности, поляризацию колебательных полос).
