Сформулируйте первый закон Гиббса-Коновалова. Проиллюстрируйте его с помощью диаграмм состояния системы с идеальными растворами и неидеальной азеотропной системы.

Окончания фазовых превращений, а также составы исчезающей и образующейся фаз. Что может быть выделено в дистилляте при ректификации выбранных жидких растворов и что останется в кубовом остатке?

Положительное отклонение от идеальности:

Можно выделить только азеотроп, в кубовом остатке будет находится компонент, присутствующий в избытке по отношению к азеотропу.

Диаграмма состояния двухкомпонентной системы А-В характеризуется максимумом на кривых «температура-состав» при постоянном давлении. Компонент А является менее летучим, чем вещество В. Схематически изобразите названную диаграмму. Укажите составы дистиллята и кубового остатка при ректификации жидкой смеси, которая более богата компонентом А по сравнению с азеотропной смесью. Какие отклонения от идеальности растворов проявляются в данной системе? Приведите необходимые пояснения.

18.Запишите уравнение, выражающее правило рычага, и назовите входящие в него величины. Проиллюстрируйте его примером T-x(y)-диаграммы кипения (при P=const) двухкомпонентной системы (диаграмму выберите в справочнике). Укажите температуру, до которой необходимо нагреть систему выбранного состава для того, чтобы мольные количества жидкой и паровой фаз были бы одинаковы.

19.Запишите уравнение, выражающее правило рычага, и назовите входящие в него величины. Проиллюстрируйте его примером диаграммы взаимной растворимости двух ограниченно растворимых друг в друге жидкостей (диаграмму выберите в справочнике).

Состав фаз, находящихся в равновесии, определяется правилом рычага: если одна фаза при изменении параметров системы разлагается на две другие фазы, то количественное соотношение образующихся фаз будет обратно пропорционально длинам отрезков от точки состава исходной фазы до точек состава образующихся фаз

Для кипения:

Произведение массы жидкой фазы на плечо, соединяющее точку опоры (а) с линией жидкости, равно произведению массы пара, на плечо, соединяющее точку (а) с линией пара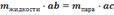

Если известна общая масса системы m, то, используя правило рычага, можно найти массы сосуществующих фаз. Выразим массу пара через общую массу системы и массу жидкости:

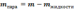
Правило рычага в этом случае примет вид:

Определив по диаграмме размер отрезков ab и ac, можно найти массу жидкости, а затем и массу пара в двухфазной области. Правило рычага используют только в двухфазной области!

Вывод з-на развед.Ост.для слаб.эл-та,мол-лы к-го диссоциируют в разбав.водном р-ре на 2 иона.Константа эл-ой дис-ции.Записать получ.ур-е с исп-ем величины молярной электропроводности.

Kд= α2*C/(1−α); α= λ/λ∞; Kд= ((λ^2/λ0^2)*C)/(1− λ/λ0) = (λ^2/λ0^2)*C*(λ0/(λ0−λ) = (λ^2*C)/(λ0^2−λ0*λ);

λ^2*C=Kд*λ0^2−Кд*λ0*λ;

λ^2*C+Кд*λ0*λ−Kд*λ0^2=0;

λ= −Кд*λ0+√(Кд^2*λ0^2+4*Кд*C *λ0^2)/2*Кд =−λ0+ λ0/2*√(1+ 4*C/Kд)

Изм-е эл.пр-ти как метод исслед.тд.св.р-ров эл-тов и ионных равновесий.

Кондуктометр.титрование.

Метод титрования, при котором точку эквивалентности фиксируют по резкому изм-ю электропроводности исследуемого раствора, наз.кондуктометрическим. Электропроводность раствора зависит от природы эл-та, его конц-ии в р-ре, природы растворителя и концентрации. Поскольку уд. электр-ть разбав.рров пропорциональна концентрации эл-та, можно, измеряя электропроводность, определить конц-цию. Практич. применение этого метода ограничено тем, что электропроводность р-ра определяется суммарной концентрацией всех ионов, находящихся в растворе. Кондук.титр.имеет большое значение при анализе окрашенных и мутных растворов. Условием применимости этого метода является существенное изм-е электропроводности в момент достижения точки эквивалентности. При титровании анализируемого в-ва стандартным р-ром титранта в случае образования нерастворимого или малодиссоциированного соединения электропроводность р-ра снижается вследствие уменьшения кол-ва ионов в рре. Наименьшее кол-во ионов, а значит и наименьшая электропроводность раствора будут в точке эквив-ти. После достижения этой точки электропроводность снова начнет возрастать вследствие избытка титранта-электролита. График титрования электропроводность - объем титранта обычно имеет вид ломаной линии, где точки перегиба (излома) соответствуют точкам эквивалентности. Форма кривой титрования зависит от природы реагирующих и образующихся веществ.

Как на основании экспериментальных данных об электрической проводимости раствора слабого электролита рассчитать теплоту его диссоциации? Укажите основные этапы этого расчета, приведите соответствующие расчетные формулы.

Электропр-ть р-ров сильных эл-тов.Зависимость моляр.эл-ой пров-ти р-ров сильных эл-тов от конц-и.Природа сил торм.при движении ионов в р-рах сильных эл-тов.Электрофор.и релаксац.эффект сниж. электропроводности в р-рах сильн.эл-тов.

Проводники II рода называются электролитами.

Осн мерой способности эл-тов проводить эл. ток является электрическая проводимость. K= 1/R =[ 1/Ом ]=[См] .

Молярная эл. проводимость λm – эл. проводимость раствора, распол-го м/у двумя электродами, располож-ми на расстоянии 1м друг от друга, причем площадь каждого электрода такова, что между ними находится 1 моль растворенного вва.

Зависимость молярной эл. проводимости от концентрации:

λ∞ предел. электр. проводимость при бесконечном разведении. В слабых электролитах λ сразу падает, т. к. при ∞ разведении α=1, а потом уменьшается.

Для слабого электролита такая зависимость молярной электропроводности от концентрации обусловлена в основном увеличением степени диссоциации с разбавлением раствора. В случае сильного электролита с уменьшением концентрации ослабляется взаимодействие ионов между собой, что увеличивает скорость их движения и, следовательно, молярную электропроводность раствора.

Ионная подвижность. В 1875 г. Колърауш проводил сопоставление молярных проводимостей при бесконечном разбавлении для пары сильных электролитов, имеющих общие ионы. Он установил, что разность молярных проводимостей между членами каждой пары с общими ионами оказывается постоянной (табл. 10.1). На этом основании Кольрауш сформулировал закон аддитивности (независимости) ионных подвижностей, названный впоследствии его именем. Закон Кольрауша гласит, что молярная проводимость электролита при бесконечном разбавлении представляет собой сумму подвижностей ионов, образующих электролит, и что эти подвижности не зависят от других ионов.

Ионная подвижность связана с молярной проводимостью данного иона при бесконечном разбавлении. Для электролита состава 1:1 (иначе, для 1 :1-электролита) типа KCl закон Кольрауша математически записывается так:

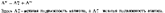
Ионная подвижность является мерой скорости, с которой данный ион перемещается через раствор. Вообще говоря, ионы с малыми ионными радиусами перемещаются медленнее, чем ионы с большими ионными радиусами. Это объясняется тем, что ион меньшего размера имеет более высокую плотность заряда и поэтому сильнее сольватируется растворителем (см. разд. 2.2). Его гидратная оболочка и, следовательно, его эффективный размер оказывается больше, чем у иона с большим ионным радиусом. Большой эффективный заряд такого иона обусловливает его малую подвижность в растворе.

Силы торможения опред-ся ионной силой р-ра, природой раств-ля и темп-ой. Для одного и того же эл-та при прочих равных усл-ях они возрастают с ув-ем конц-ции р-ра. Эффект электрофоретического торможения возникает вследствие того, что центр-ый ион и его ионная атмосфера обладают противоположными по знаку зарядами. При наложении на р-р эл-та электричго поля ионы, входящие в ионную атмосферу, движутся в навстречу центральному иону. След-но, движущийся центр-ый ион находится под влиянием тормозящей силы, названной электрофоретической силой трения, что приводит к снижению его скорости. Эффект релаксационного торможения,возникает вследствие того, что при движении иона в электрическом поле нарушается центральная симметрия ионной атмосферы: перемещение иона сопровождается разрушением ионной атмосферы в одном положении иона и формированием ее в другом, новом. Данный процесс протекает с конечной скоростью в течение некоторого времени, называемого временем релаксации. Позади движущегося иона, потерявшего центральную симметрию, всегда будет некоторый избыток заряда противополож. знака. Силы электростатич-го притяжения, возникающие при этом, будут тормозить движение иона. В электрических полях высокого напряжения (~107 В/м) скорость движения ионов становится настолько большой, что ионная атмосфера не успевает образоваться, вследствие чего оба тормозящих эффекта отсутствуют (эффект торможения Вина). В электрических полях высокой частоты (∼104 Гц) центр-ый ион очень быстро колеблется не выходя за пределы окружающей его атмосферы, которая не успевает разрушиться. Вследствие этого релаксационное торможение исчезает и остается лишь электрофоретическое торможение (эффект Дебая – Фалькенгагена).

Имеются данные о зависимости электропроводности р-ра от конц-ции эл-та.Какие граф.зависимости необ-мо построить,чтобы получить ответ на вопрос- явл-ся дан.эл-т сильным или слабым? Какие хар-ки р-ров эл-тов при этом могут быть определены?

Осн мерой способности эл-тов проводить эл. ток является электрическая проводимость. K= 1/R =[ 1/Ом ]=[См] .

Для проводников I рода R=ρ*l/S . Отсюда K= 1/R = S/(ρ*l) =γ*S/l , где γ — удельная электрическая проводимость — эл. проводимость объема р-ра, заключ-о м/у двумя параллельными электродами площадью 1 м2 каждый, расположенные на расстоянии 1м друг от друга. Молярная эл. проводимость λm – эл. проводимость раствора, распол-го м/у двумя электродами, располож-ми на расстоянии 1м друг от друга, причем площадь каждого электрода такова, что между ними находится 1 моль растворенного вва. Эквивалентная эл. проводимость λэкв – эл. проводимость раствора, расположенного между двумя электродами, расположенными на расстоянии 1м друг от друга, причем площадь каждого электрода такова, что между ними находится 1 г-экв растворенного вещества.

λm= γ/C =γ*V , C – молярная концентрация [моль/м3 ], V – разведение, V = 1/C.

γ = 1/ρ ,[ 1/(Ом*м)],λm=[ м2/(Ом*моль)]

λэкв= λm*f , где f – фактор эквивалентности, выраженный в целых числах. Зависимость удельной эл. проводимости от концентрации:

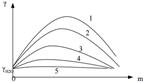1-HCl

2-KOH

3-KCl

4-LiCl

5-CH3-

COOH

Сначала при повышении конц.уд.эл. проводимость растет почти прямо пропорционально конц, т. к. повышается кол-во переносчиков заряда. При достижении определенной точки она начинает падать из-за двух факторов: 1) электрофоретическое торможение; 2) релаксационное торможение. В слабых электролитах она падает при уменьшении степень диссоциации вследствие роста концентрации. Зависимость молярной эл. проводимости от концентрации:

λ∞ предел. электр. проводимость при бесконечном разведении. В слабых электролитах λ сразу падает, т. к. при ∞ разведении α=1, а потом уменьшается.

20. Приведите аналитические выражения двух законов Кольрауша: уравнения квадратного корня, и закона независимого движения ионов. Для каких электролитов (слабых или сильных) и при каких условиях справедливы эти выражения?

А-функ

2 торм

ожений

λ∞ предел. электр. проводимость при бесконечном разведении.

Для сильн:

Моляр.пров-ть эл-та = сумме предел.подвиж. анионов и катионов.

Λ₊⁰=F*U₊⁰;F-число Фарадея;U-абс.скор.движ.ионов

Для сильн.эл-тов в разб.р-рах

21.Электрическая проводимость растворов электролитов при бесконечном разведении. Расположите перечисленные системы в порядке возрастания молярной электрической проводимости водных растворов при бесконечном разведении и температуре 25оС: (дан ряд водных растворов электролитов). Приведите обоснование ответа.

Для слабого электролита такая зависимость молярной электропроводности от концентрации обусловлена в основном увеличением степени диссоциации с разбавлением раствора. В случае сильного электролита с уменьшением концентрации ослабляется взаимодействие ионов между собой, что увеличивает скорость их движения и, следовательно, молярную электропроводность раствора. Последнюю связывает с абсолютными скоростями движения катионов и анионов U₊ и U_– уравнение Аррениуса:

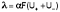
Ф. Кольрауш показал, что в молярную электропроводность бесконечно разбавленных растворов электролитов каждый из ионов вносит свой независимый вклад, и λ_o является суммой молярных электропроводностей катиона и аниона λ₊ и λ_– (т.н. подвижностей ионов), и сформулировал закон независимости движения ионов:

Молярная электропроводность при бесконечном разведении равна сумме электролитических подвижностей катиона и аниона данного электролита.

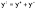
Подставив в это выражение уравнение Аррениуса (III.35) и приняв, что при бесконечном разведении степень диссоциации α равна единице, получим:

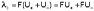
Отсюда

;

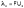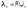
Электролитическая подвижность является важнейшей характеристикой иона, отражающей его участие в электропроводности раствора.

1-HCl

2-KOH

3-KCl

4-LiCl

5-CH3-

COOH

22.Закон независимого движения ионов. Расположите перечисленные ниже системы в порядке возрастания молярной электрической проводимости водных растворов при бесконечном разведении и температуре 25оС: (дан ряд водных растворов электролитов).

Для сильн: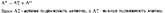

Моляр.пров-ть эл-та = сумме предел.подвиж. анионов и катионов.

Λ₊⁰=F*U₊⁰;F-число Фарадея;U-абс.скор.движ.ионов

Для сильн.эл-тов в разб.р-рах

1-HCl 2-KOH 3-KCl 4-LiCl 5-CH3COOH

23.Методы определения молярной электрической проводимости растворов слабых и сильных электролитов при бесконечном разведении.

Для сильных эл-тов можно построить график в координатах

График будет являться прямой линией.Экстраполировав его на верт.ось получим значение λ₀

Для слаб.эл-тов ее вычисляют по з-ну независ-ти движ.ионов.Кальрауша.

Для этого необходимо найти Λ₊⁰ Λ_-⁰ отдельно для каждого типа ионов,исследуя сильн.эл-ты,сод.эти ионы.

Скорость движения, абсолютная скорость движения (подвижность) иона. Влияние природы иона и природы растворителя на подвижность иона. Связь предельной молярной электрической проводимости иона с его абсолютной скоростью движения (подвижностью).

Абс.скорость движ.иона – скор.передвижения иона к электроду, отнесенная к единице напряж-ти эл.поля.

U[см2/(В*с)] Подвижность ионов – скорость достигаемая ионами в поле напряж-тью 1В/см

Скорость движения ионов в р-ре зависит от их пр-ды,темп-ры,и пр-ды раств-ля, а именно: 1.Пр-да иона опред-ся его радиусом r и зарядом z.Эти 2 фактора хар-ют поляризующую способность ионов по отн-ию к растворителю.В р-рах скорость движ.ионов опр-ся размерами сальват-ых ионов.Чем меньше радиус иона и больше заряд, тем большим поляризующим действием ион обладает. 2)пр-да р-ля хар-ся диэлектрич.постоянной дельтаЕ.С ум.вел.дельтаЕ падает способность р-ля сальватировать ионы в р-ре; электропров-ть р-ра ум-ся,поскольку происходит ум.степени диссоциации в-в в малополярных р-лях.3)С ростом темп. Эл.пров-ть ув-ся на каждый градус на 2%.

Предельное значение λº, отвечающее молярной электрической проводимости гипотетического бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами, можно выразить соотношением:

λº = F(U₀₊ + U_0-).

25.Зависимость подвижности (абсолютной скорости движения) иона от его заряда и размеров (радиуса). Кристаллографический радиус иона Li+ меньше, чем иона K+. Какой из ионов дает больший вклад в электропроводность водных растворов хлоридов солей этих металлов при бесконечном разведении при одной и той же температуре? Для обоснования ответа приведите уравнения, связывающие между собой названные величины.

Пр-да иона опред-ся его радиусом r и зарядом z.Эти 2 фактора хар-ют поляризующую способность ионов по отн-ию к растворителю.В р-рах скорость движ.ионов опр-ся размерами сальват-ых ионов.Чем меньше радиус иона и больше заряд, тем большим поляризующим действием ион обладает.

Чем меньше кристаллограф.радиус, тем более сильное поле создает ион и тем в большей степени он гидратирован.Поэтому радиус гидр.иона Li больше, чем гидр.и.Na. К больше,чем Li.Однако, если собств.размер иона возрастает настолько,что прочная гидратная оболочка вокруг него уже не удерживается, то при дальнейшем увеличении кристиллограф. Радиуса следует ожидать уменьшения подвижности.Эта закономерность наблюд-ся у катионов(при переходе от Cs к [(CH3)4N], и анионов(от Br к I и далее к CH3COO)

26.Числа переноса ионов в растворе данного электролита, их связь с электрической проводимостью ионов. Сравните числа переноса катиона и аниона в растворе … (дан конкретный электролит). Эстафетный механизм переноса электрического тока ионами гидроксония и гидроксила.

Число переноса иона ti – это отношение количества электричества, перенесенного ионами, к общему количеству электричества, прошедшему через раствор. t(i)= I(i)/∑I(i)=I(i)/I;∑t(i)=1 .

t₊= I₊/I = I₊/(I₊+I_-)= u₊/(u₊+u_-)= λ₊/(λ₊+λ_-)= λ₊/λ ;t_-= λ_-/λ.

Эстафет.механизм переноса:

Ион водорода как бы прыгает по молекулам воды, преодолевая гораздо большее расстояние, чем мог бы преодолеть за счет собственного движения. Ион водорода присоединяется к молекуле воды, образуя ион гидроксония. Противоположный атом водорода отщепляется и образуется ион водорода, который притягивается следующей молекулой воды и так далее. С ионом OH- тоже самое, только ион водорода двигается в обратную сторону. Получается, что двигается OH-.

27.Как по данным об электрической проводимости растворов сильных электролитов определить электрическую проводимость при бесконечном разведении для раствора слабого электролита в том же растворителе? Какой закон лежит в основе метода определения? Проиллюстрируйте процедуру расчета каким-либо произвольным примером.

Эл.проводимость слаб.эл-тапри бесконеч.разведении:

Для этого необходимо найти Λ₊⁰ Λ_-⁰ отдельно для каждого типа ионов,исследуя сильн.эл-ты,сод.эти ионы.

В основе лежит закон независимости движения ионов Кальрауша.

Растворы сильных электролитов. Основные положения теории Дебая-Хюккеля. Зависимость среднего ионного коэффициента активности от ионной силы раствора в разбавленных и концентрированных растворах сильных электролитов.

Теория Д-Х:1. Ионы рассматриваются в виде материальных точек. 2. Элты диссоциированы полностью. 3. Растворитель представляет собой непрерывную среду с диэлектрической проницаемостью ε. εр-ра = εр-рителя. 4. М/у ионами действуют только силы кулоновского взаимодействия. Основные допущения теории: 1. Применима только для сильных электролитов. 2. В ионной атмосфере распределение ионов подчиняется законам классической статистики. 3. Ионная атмосфера рассматривается как непрерывная статическая среда. В разбавленных растворах сильных электролитов среднеионные коэффициенты активности у электролитов одного и того же типа одинаковые при равной ионной силе раствора.

Ионная сила-полусумма произведений ионных конц-й в р-ре на квадрат их валентности.

I=1/2∑zi^2*mi,где zi – заряд иона, mi – моляльность иона. Согласно первому приближению Д-Х(предельный закон): lgγ±=−A∣z₊ z_-∣√I , где I – ионная сила раствора,

z₊ z_—заряды ионов; A=(1,825∗10^6)/(ε T )^3 /2 , где ε — диэлектрическая проницаемость, T – температура. Для воды при 25 градусах A = 0,509. Первое приближение описывает растворы с концентрацией 0,01 — 0,03 моль/кг. В концентрированных растворах первое приближение заметно не совпадает с экспериментальными данными, поэтому используют второе и третье приближения, учитывающие расстояние наибольшего сближения ионов a, а также дополнительные константы: lg γ ±= −A*∣z₊ z_-∣√ (I)/(1+Ba √I) , B= (50,3∗10^8)/(ε*T)^1/2; lg γ ±= −A∣z+ z−∣√ I/(1+Ba*√ I) +CI Второе приближение хорошо описывает растворы с концентрацией до 0,1М, третье — до 1М.

Запишите определительные уравнения для средних ионных величин: коэффициента активности, активности, моляльности. Как связана средняя ионная активность с моляльной концентрацией раствора и активностью электролита. Приведите соответствующие выражения для электролита валентного типа «(дан тип)».

Активность — это эффективная концентрация ионов в растворе, т. е. концентрация с учетом отклонений поведения системы от идеальности.

Коэффициент активности – мера отклонения поведения р-ра от идеального отклонения м.б. обсуловлены разл-мы хим.и физ.причинами. Для иона,как и для комп-та в р-ре: µ_i=µ_i⁰+RTlnc_i C-конц-я i-го иона в идеал.р-ре, то для реал.р-ра будем иметь µ_i=µ_i⁰+RTlnа_i =µ_i⁰+RTlnc_i + RTlnf_i ,где а_i =c_i f_i -активность i-го иона в р-ре; f-коэф-т активности. Тогда энергия вз-ия иона с окруж.его ионами в расчете на 1 моль ионов равна: Е=( µ_i^’- µ_i )= RTlnf_i

Связь активности эл-та с акт.иона: а_с=а₊^v+*a_-^v-,a_c – активность эл-та. а₊ a_- -активности пол и отр ионов.

Средний ионный акт:а(+-)=(а₊^v+*a_-^v-)^1/v

а(+-)=а_с^(1/v)

Сред.ион.коэф.актив-ти(γ(+-)):γ(+-)=(γ₊^v+*γ_-^v-)^1/v

Активность связана с конц: а=γ*m

Ср.ион.моляльность(m(+-): m(+-)=(m₊^v+*m_-^v-)^1/v

Правило ионной силы раствора. Предельный закон Дебая-Хюккеля как теоретическое обоснование этого правила. В какой области концентраций им можно пользоваться? Изобразите схематически график зависимости, соответствующей предельному закону.

Ионная сила-полусумма произведений ионных конц-й в р-ре на квадрат их валентности.

I=1/2∑zi^2*mi,где zi – заряд иона, mi – моляльность иона. Согласно первому приближению Д-Х(предельный закон): lgγ±=−A∣z₊ z_-∣√I , где I – ионная сила раствора,

z₊ z_—заряды ионов; A=(1,825∗10^6)/(ε T )^3 /2 , где ε — диэлектрическая проницаемость, T – температура. Для воды при 25 градусах A = 0,509. Первое приближение описывает растворы с концентрацией 0,01 — 0,03 моль/кг. В концентрированных растворах первое приближение заметно не совпадает с экспериментальными данными, поэтому используют второе и третье приближения, учитывающие расстояние наибольшего сближения ионов a, а также дополнительные константы: lg γ ±= −A*∣z₊ z_-∣√ (I)/(1+Ba √I) , B= (50,3∗10^8)/(ε*T)^1/2; lg γ ±= −A∣z+ z−∣√ I/(1+Ba*√ I) +CI Второе приближение хорошо описывает растворы с концентрацией до 0,1М, третье — до 1М.

1приближение:0-0,001,2прибл:0,001-0,1,3прибл:0,1-1

Правило ионной силы Льюиса-Рендела: в разбавленном растворе среднеионный коэффициент активности зависит только от ионной силы раствора и не зависит от конкретного вида других ионов, находящихся в растворе. Правило справедливо при концентрациях 0,01-0,02 моль/кг, приближенно — до 0,02 моль/кг.

Экспериментальная зависимость среднего ионного коэффициента активности электролита от корня (квадратного) из ионной силы раствора в широкой области концентраций. На том же графике представьте зависимость, отвечающую предельному закону Дебая-Хюккеля. В какой области концентраций он выполняется?

lgγ(i)=-Az(i)^2*√ I

Пред.з-н ДХ соответствует экспер.данным только конц.менее 0,01

Правило ионной силы Льюиса-Рендела: в разбавленном растворе среднеионный коэффициент активности зависит только от ионной силы раствора и не зависит от конкретного вида других ионов, находящихся в растворе. Правило справедливо при концентрациях 0,01-0,02 моль/кг, приближенно — до 0,02 моль/кг.

Приведите уравнения, описывающие зависимость среднего ионного коэффициента активности от корня (квадратного) из ионной силы раствора согласно трем приближениям теории Дебая-Хюккеля. Приведите схематически зависимости для каждого из приближений и сопоставьте их с реальной зависимостью (в названных координатах), построенной на основании экспериментальных данных.

Ионная сила-полусумма произведений ионных конц-й в р-ре на квадрат их валентности.

I=1/2∑zi^2*mi,где zi – заряд иона, mi – моляльность иона. Согласно первому приближению Д-Х(предельный закон): lgγ±=−A∣z₊ z_-∣√I , где I – ионная сила раствора,

z₊ z_—заряды ионов; A=(1,825∗10^6)/(ε T )^3 /2 , где ε — диэлектрическая проницаемость, T – температура. Для воды при 25 градусах A = 0,509. Первое приближение описывает растворы с концентрацией 0,01 — 0,03 моль/кг. В концентрированных растворах первое приближение заметно не совпадает с экспериментальными данными, поэтому используют второе и третье приближения, учитывающие расстояние наибольшего сближения ионов a, а также дополнительные константы: lg γ ±= −A*∣z₊ z_-∣√ (I)/(1+Ba √I) , B= (50,3∗10^8)/(ε*T)^1/2; lg γ ±= −A∣z+ z−∣√ I/(1+Ba*√ I) +CI Второе приближение хорошо описывает растворы с концентрацией до 0,1М, третье — до 1М.

lgγ(i)=-Az(i)^2*√ I

Произведение растворимости малорастворимых соединений. Изменятся ли (и если да, то как) произведение растворимости и растворимость малорастворимой соли, если в водный раствор этого соединения ввести посторонний сильный электролит, не имеющий общих ионов с малорастворимой солью. Приведите обоснование ответа.

Произведение растворимости — произведение конц-ий ионов малорастворимого в-ва в его насыщенном р-ре при пост. Темп-ре и давлении. ПР — величина постоянная в данных условиях. Константа диссоциации вычисляется по формуле: Kд= [A+]^а [ B- ]^b / [ AB] . Если считать, что вещество малорастворимо, то можно пренебречь изменением концентрации исходного вещества. Тогда Kд=ПР=[ A+]^a[B-]^b . При относительно высоких концентрациях необходимо использовать не концентрации ионов, а их активности: ПР=a₊^v+ *a_-^v- . ПР= a₊^v+ *a_-^v- = m₊^v+ γ₊^v+ *m_-^v- *γ_-^v- = v₊^v+ *v_-^v- m^v *γ^v +-

При введении в раствор стороннего электролита, не имеющего общих ионов с рассматриваемым веществом, ПР не изменится, т. к. он зависит только от p и T

Растворимость малорастворимых электролитов. Изменятся ли (и если да, то как) произведение растворимости и растворимость малорастворимой соли, если в раствор ввести посторонний сильный электролит, не имеющий общих ионов с малорастворимой солью. Приведите обоснование ответа.

Растворимость вещества можно выразить из уравнения ПР: m= 1/γ±*(ν)√ ПР/( v₊^v+ *v_-^v-) , где γ ±=−A∣z + z-∣√ I . Поскольку ионная сила зависит от всех ионов, входящих в раствор, то при добавлении хорошо растворимого вещества, ионная сила сильно увеличится, вследствие чего увеличится среднеионный коэффициент активности, а растворимость уменьшится. Правило ионной силы Льюиса-Рендела: в разбавленном растворе среднеионный коэффициент активности зависит только от ионной силы раствора и не зависит от конкретного вида других ионов, находящихся в растворе. Правило справедливо при концентрациях 0,01-0,02 моль/кг, приближенно — до 0,02 моль/кг.

При добавлении в р-р сильного эл-та, не имеющего общих ионов с нашей малораств.солью ПР не изм-ся,т.к.зависит только от Т и р.Раств-ть уменьшится, т.к. увеличится I.

Растворимость малорастворимых электролитов. Приведите выражение для произведения растворимости соединения AB (дан конкретный электролит). Каким образом изменяется растворимость этой малорастворимой соли при добавлении в раствор индифферентного электролита (т.е. электролита не имеющего общих ионов с малорастворимой солью)? Дайте обоснованный ответ.

Растворимость вещества можно выразить из уравнения ПР: m= 1/γ±*(ν)√ ПР/( v₊^v+ *v_-^v-) , где γ ±=−A∣z + z-∣√ I . Поскольку ионная сила зависит от всех ионов, входящих в раствор, то при добавлении хорошо растворимого вещества, ионная сила сильно увеличится, вследствие чего увеличится среднеионный коэффициент активности, а растворимость уменьшится. Правило ионной силы Льюиса-Рендела: в разбавленном растворе среднеионный коэффициент активности зависит только от ионной силы раствора и не зависит от конкретного вида других ионов, находящихся в растворе. Правило справедливо при концентрациях 0,01-0,02 моль/кг, приближенно — до 0,02 моль/кг.

Произведение растворимости — произведение конц-ий ионов малорастворимого в-ва в его насыщенном р-ре при пост. Темп-ре и давлении. ПР — величина постоянная в данных условиях. Константа диссоциации вычисляется по формуле: Kд= [A+]^а [ B- ]^b / [ AB] . Если считать, что вещество малорастворимо, то можно пренебречь изменением концентрации исходного вещества. Тогда Kд=ПР=[ A+]^a[B-]^b . При относительно высоких концентрациях необходимо использовать не концентрации ионов, а их активности: ПР=a₊^v+ *a_-^v- . ПР= a₊^v+ *a_-^v- = m₊^v+ γ₊^v+ *m_-^v- *γ_-^v- = v₊^v+ *v_-^v- m^v *γ^v +-

При добавлении индефферент.эл-та I ув-ся,=> γ ±=−A∣z + z-∣√I сред.коэф.активности ув-ся=> растворимость уменьшится.

Возникновение скачка потенциала на границе раздела проводников I и II рода. Обратимые электроды и обратимые гальванические элементы. Условная запись правильно разомкнутого гальванического элемента. Электродвижущая сила (ЭДС) гальванического элемента.

Потенциал µ(cu2+пластина) > µ(cu2+р-ра)=>пласт.в р-р до выравнивания потенциала=>возн.эл.слой на границе раздела ж-тв=>возникает скачок потенциала от Ме и ж-ти.Явление возник-я скачка потенциала на границе раздела фаз лежит в основе работы гальв.эл-тов.

Электроды могут быть обратимыми по катиону или по аниону. По катиону обратимы электроды 1 рода с металлической пластинкой и газовые электроды, которые в растворе дают катион. По аниону — 1 рода с неметаллической пластинкой, газовые, которые в растворе дают анион, и электроды II рода. Гальванический элемент называется обратимым, если при пропускании через него тока в обратном направлении в нем происходят обратные химические реакции. Такой гальванический элемент составлен из двух обратимых электродов. Условная запись: слева записывается электрод, имеющий более отрицательный стандартный электродный потенциал; границы фаз обозначаются сплошной вертикальной чертой, граница растворов обозначается одинарной вертикальной пунктирной прямой, если есть диффузионный потенциал, либо двойной вертикальной пунктирной прямой, если он отсутствует. Исключение составляет водородный электрод, который всегда располагается слева. Пример правильно разомкнутого гальванического элемента: Pt, H2 | HCl || CuSO4 | Cu | Pt ЭДС гальванического элемента равна разности электродных потенциалов составляющих его электродов. Согласно принятой форме записи гальванического элемента, его ЭДС равна разности электродных потенциалов правого и левого электродов: E = Eпр — Eлев > 0

40.Приведите пример химического гальванического элемента, составленного из газового электрода и электрода второго рода, электрохимическая цепь без жидкостных соединений - «без переноса». Запишите уравнения электродных полуреакций и уравнение химической реакции, за счет энергии которой вырабатывается электрическая энергия данным элементом.

Примером такой цепи является водород-хлорсеребряный элемент

Pt | (H₂) | HCl | AgCl | Ag, (I)

кот состоит из водородного и хлорсеребряного эл-дов, погруженных в р-р хлороводорода. При работе в таком элементе протекают эл-дные реакции: 1/2H₂(газ)®H⁺(р-р) + e; AgCl (тв) + e ®Ag (тв) + Cl^–(р-р)

Т о, суммарный процесс представляет собой химическую реакцию: 1/2H₂(газ) + AgCl (тв)®Ag (тв) + Н⁺(р-р) + Cl^–(p-p);

ЭДС такой цепи равна разности потенциалов хлорсеребряного и водородного электродов. Учитывая ур-ия получим

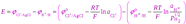
Разность стандартных потенциалов хлорсеребряного и водородного эл-дов дают стандрт ЭДС цепи Е^о, но т к стандартный потенциал водородного эл-да принят равным нулю, то Е^о равна стандартному потенциалу хлорсеребряного электрода. Если давление водорода =1, то

.

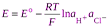Если хлороводород полностью диссоциирован в р-ре, то произведение активностей ионов водорода и хлора можно заменить средней ионной активностью 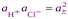, тогда

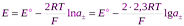
Газовые электроды, водородный электрод. Вывод и анализ уравнения, выражающего зависимость потенциала водородного электрода от активности водородных ионов и давления молекулярного водорода. Область применения водородного электрода.

Газовые электроды - пластинка инертного металла, омываемая газом, опущенная в раствор, содержащий ионы этого газа. Пример электрода: Pt, H2 | H+ Уравнение полуреакции: H⁺ + e → ½ H2 Уравнение Нернста: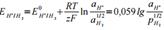

Е⁰=0В.

Водород.эл-д-пластинка или проволока из Ме,хорошо поглощ.газообр.водород,насыщ.водородом(при атм.давл) и погруженный в вод.р-р,содерж.ионы водорода.

Pt, H2 | H+ Уравнение полуреакции: H+ + e →<= ½ H2 Уравнение Нернста:

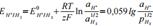
z=1,E=0В

Применение вод.эл-да в произ-ве очень неудобно,потому что связано с подачей газообр.Н2.Преимущество:широкая область применимости.М.использовать в большом диапазоне темп,давл, и рН, а также во многих неводных или частично водных р-рах.

Водородный электрод. Условная шкала потенциалов. Уравнение Нернста для потенциала водородного электрода. Зависимость потенциала электрода от рН раствора и давления молекулярного водорода. Область применения водородного электрода.

Водород.эл-д-пластинка или проволока из Ме,хорошо поглощ.газообр.водород,насыщ.водородом(при атм.давл) и погруженный в вод.р-р,содерж.ионы водорода.

Pt, H2 | H+ Уравнение полуреакции: H+ + e →<= ½ H2 Уравнение Нернста:

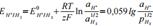
z=1,E=0В

Применение вод.эл-да в произ-ве очень неудобно,потому что связано с подачей газообр.Н2.Преимущество:широкая область применимости.М.использовать в большом диапазоне темп,давл, и рН, а так