Статистический характер второго закона термодинамики. энтропия и термодинамическая вероятность

Энтропия имеет статистический характер, следовательно, можно говорить и о статистическом характере 2-го закона ТД. Так как равномерное распределение частиц (по молекулярно-кинетической теории) является наиболее беспорядочным, наиболее хаотичным, то с увеличением энтропии растёт хаос в системе. Таким образом, естественная тенденция самопроизвольного процесса направлена к состоянию с более высокой энтропией [1].

2-ой закон ТД – статистический закон. Несамопроизвольные (отрицательные) процессы в макроскопических системах являются не невозможными, а крайне маловероятными событиями.

Как установил Клаузиус, энтропия остаётся без изменений, если в изолированной системе протекают обратимые процессы, и возрастает, если в изолированной системе протекают самопроизвольные (необратимые) процессы. Следовательно, критерием самопроизвольного протекания процесса в изолированной системе является увеличение энтропии [2].

∆S_изол >0 (3.1)

Пределом самопроизвольного процесса в изолированной системе является достижение равновесия, которому соответствует максимум энтропии:

mахS – ТДР; (3.2)

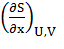= 0 и 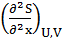> 0 (3.3)

где:

х – какой-либо параметр (Т, Р, концентрация).

Энтропия идеального кристаллического вещества при абсолютном нуле равна нулю:

S_o = 0 (3.4)

(М. Рlаnck, 1912). Иногда это утверждение называют третьим законом ТД в формулировке Планка.

Энтропия растёт с увеличением температуры: S_пара > S_ж > S_тв.

РАСЧЕТ ИЗМЕНЕНИЯ ЭНТРОПИИ ВЕЩЕСТВА «А» В ЗАДАННОМ ИНТЕРВАЛЕ ТЕМПЕРАТУР

Исходные данные к работе:

Вещество «А»: С₂Н₃ClО₂ (хлоруксусная кислота)

Температуру плавления, температуру кипения, теплоемкость в твердом состоянии, теплоемкость в жидком состоянии, теплоемкость в газообразном состоянии, теплоту плавления, теплоту испарения, ищем по «Справочнику химика, т.1.» [4].

Молярную массу находим по таблице Менделеева

М – 94,5 г/моль;

m – 15 (кг)

Т₁ – 423К;

Т₂ – 313К;

Т_пл – 335,45К;

ΔН_пл – 19,37·10³ Дж/моль;

Т_исп – 461,71К;

ΔН_исп – 12,28·10³ Дж/моль;

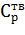– 86,7 Дж/К моль;

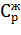–83,5 Дж/К моль;

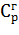–35,8 Дж/К моль;

РЕШЕНИЕ

Весь процесс охлаждения можно разделить на несколько стадий:

4) процесс испарения при Т_исп = 461,71К;

3) охлаждение 15 кг жидкого С₂Н₃ClО₂ от 461,71К до Т_пл = 335,45К;

2) плавление вещества при Т_пл= 335,45К;

1) охлаждение 15 кг твердого С₂Н₃ClО₂ от Т_пл = 335,45К до Т₂= 313К;

Соответственно этому:

ΔS=Δ4+ Δ3+ Δ2+ Δ1 Дж/К; (4.1)

Рассчитаем ΔS для каждой стадии, Дж/К:

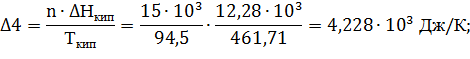
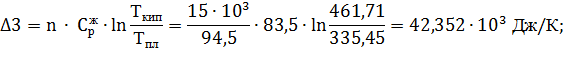
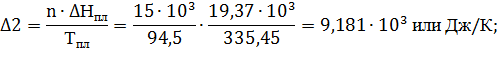
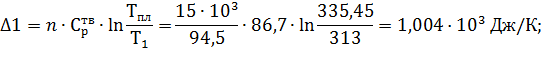
Исходя из этого:

ΔS= Δ4+ Δ3+ Δ2+ Δ1= 4,228·10³+42,352·10³+9,181·10³+1,004·10³=56,765·10³ Дж/К.

ЗАКЛЮЧЕНИЕ

Данная курсовая работа выполнена по дисциплине: «Физическая химия в принтмедиаиндустрии», на тему: «Расчет изменения энтропии вещества «А» в заданном интервале температур».

В данной курсовой работе была показана зависимость энтропии от изменения температуры: с увеличением температуры, энтропия увеличивается. Также было рассчитано изменение энтропии вещества в заданном интервале температур. В качестве исследуемого вещества использовался С₂Н₃ClО₂ (хлоруксусная кислота). Было выявлено, что именно процесс испарения вносит наибольший вклад в изменение энтропии.

Помимо расчетного задания, в курсовой работе были рассмотрены вопросы, подлежащие разработке, а именно: второй закон термодинамики и направленность физико-химических процессов; расчет изменения энтропии вещества в различных процессах. Определение абсолютного значения энтропии; статистический характер второго закона термодинамики. Энтропия и термодинамическая вероятность.