Промышленных регуляторов
Лекция по АТПП № – Настройки 4
ИНЖЕНЕРНЫЕ МЕТОДЫ ВЫБОРА И РАСЧЕТА
ОПТИМАЛЬНЫХ НАСТРОЕК
ПРОМЫШЛЕННЫХ РЕГУЛЯТОРОВ
2.3.5. Критерий Kкр и расширенные АФХ (введение критерия Kc)
Выше был обоснован критерий Kкр, но при этом умалчивалось, что согласно ему, система должна быть выведена на границу области устойчивости, что, естественно, не допустимо. Фактически, настраивая АСР по критерию Kкр, мы имеем возможность выбрать коэффициент усиления системы из максимально возможного диапазона его значений, ограниченного максимальным критическим коэффициентом усиления, причем для создания работоспособной АСР он будет меньше этого максимально возможного значения.
При этом, т.е. при введении дополнительных ограничений на систему, показатели качества АСР могут оказаться не самими лучшими при настройке регулятора по критерию Kкр. Например, введя дополнительные ограничения на требуемые запасы устойчивости системы по модулю и фазе, т.е.
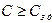 и
и 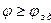 (2.101)
(2.101)
лучших показателей можно добиться при не выполнении критерия Kкр.
С другой стороны , для ряда объектов, настроив систему по Kкр, можно вообще не обеспечить желаемых запасов (2.101), что приведет к неудовлетворительному качеству регулирования. Для таких объектов лучших показателей качества можно достичь, если настроить систему на максимально возможный коэффициент усиления системы при требуемых ограничениях, хотя критический коэффициент усиления системы оказывается в этом случае меньше максимального. Такой подход назовем расчетом АСР по критерию Kc.
Для примера рассмотрим расположение параметров ПИ регулятора при настройке АСР по критериям Kкр и Kc на линиях равной степени затухания при Ψ=0, Ψ=0.75(m=0.221) и Ψ=0.9(m=0.366). Расчетные данные по системе заимствованы нами из [15] для объекта первого порядка с запаздыванием с
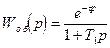
при τ=20 с и T1=100 с и представлены в таблице 2.3.
Таблица 2.3. Расчетные данные для АСР с ПИ-регулятором и объектом с 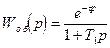 при τ=20 с, T1=100 с
при τ=20 с, T1=100 с
| ψ=0 | ψ=0.75 | ψ=0.9 | ||||||
| ω, c-1 | Kp | Kp/Tиз, c-1 | ω, c-1 | Kp | Kp/Tиз, c-1 | ω, c-1 | Kp | Kp/Tиз, c-1 |
| 0.020 | 0.14 | 0.045 | 0.015 | 0.154 | 0.024 | 0.010 | 0.09 | 0.014 |
| 0.030 | 0.87 | 0.091 | 0.020 | 0.66 | 0.040 | 0.015 | 0.52 | 0.024 |
| 0.040 | 2.17 | 0.140 | 0.030 | 1.76 | 0.073 | 0.020 | 1.07 | 0.038 |
| 0.050 | 3.67 | 0.177 | 0.040 | 2.87 | 0.101 | 0.030 | 2.14 | 0.066 |
| 0.060 | 5.23 | 0.186 | 0.050 | 3.88 | 0.110 | 0.040 | 3.05 | 0.083 |
| 0.070 | 6.73 | 0.152 | 0.060 | 4.70 | 0.090 | 0.050 | 3.74 | 0.079 |
| 0.080 | 8.03 | 0.061 | 0.070 | 5.24 | 0.035 | 0.060 | 4.13 | 0.046 |
| 0.085 | 8.56 | 0.009 | 0.075 | 5.38 | -0.007 | 0.070 | 4.21 | -0.017 |
Результаты представлены также в виде линии границы устойчивости (Ψ=0) и линий заданного запаса устойчивости (ψ=0.75 и ψ=0.9) в плоскости параметров настройки Kp и Kp /Tиз ПИ-регулятора на рис. 2.26.
Соответствующие линии для ψ=0.75 и ψ=0.9 построены исходя из понятия расширенных АФХ [15], а линия для ψ=0 является кривой Д-разбиения в плоскости двух параметров регулятора. В этих координатах настройке АСР по критерию Kкр, как будет показано ниже, соответствуют настройки лежащие на линии Tиз=const, проходящей через максимум значения Kp /Tиз на линии ψ=0, (точка 1 на рис. 2.26). При ψ=0.75 и ψ=0.9 соответственно получим параметры настройки ПИ-регулятора, отвечающие точкам 2 и 3. В тоже время критерию Kc для ψ=0.75 будут соответствовать параметры ПИ-регулятора, отвечающие точке 4 с максимумом отношения Kp /Tиз при ψ=0.75, а для ψ=0.9 - точке 5 с максимумом Kp /Tиз при ψ=0.9.
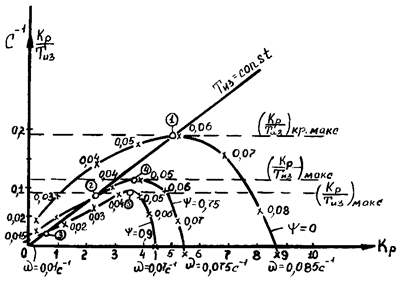
Рис. 2.26. Расположение параметров настройки ПИ-регулятора при настройке АСР по критериям Ккр и Кс
Вид переходных процессов в АСР для настроек, отвечающих соответствующим точкам, приведен на рис. 2.27. Как видно, процессы, отвечающие точкам 2,3 не являются лучшими в сравнении, соответственно, с процессами, отвечающими точкам 4,5 (последние практически совпадают).
Допустив в соответствии с гипотезой об эквивалентной АСР второго порядка, что C и φ, а также степень затухания ψ однозначно связаны с коэффициентом колебательности системы m, также воспользуемся понятием расширенных АФХ для обеспечения в АСР требуемых ограничений в виде запасов по модулю и фазе, или заданной степени затухания.
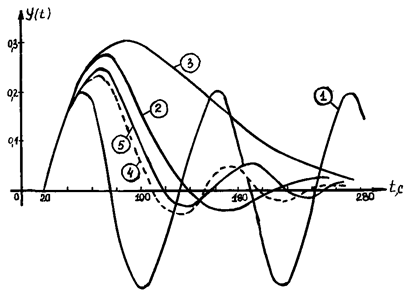
Рис. 2.27. Вид переходных процессов в АСР при различных параметрах настройки регулятора
Напомним, что расширенную АФХ получают путем замены в передаточных функциях оператора p на -mω+jω=(j-m)ω, где m – коэффициент колебательности . Соответствующие АФХ будем обозначать как W(m,jω).
m - коэффициент колебательности
В общем случае для АСР m определяют как отношение действительной части к мнимой для ближайшей к мнимой оси пары комплексно-сопряженных корней характеристического уравнения замкнутой системы. Для случая колебательного звена
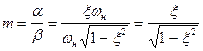 (2. 12)
(2. 12)
Графики зависимостей σ/K от ξ и m от ξ представлены на рис. 2.8г и 2.8д соответственно. Как видно с ростом ξ от 0 к 1 σ/ K убывает, а m - возрастает, т. е. котангенс угла γ все более возрастает, а процесс становится все менее колебательным и при ξ > 1 становится апериодическим.
В числе следующих показателей качества рассмотрим:
а) степень затухания - ψ
Показатель вводится для суждения о колебательности переходной характеристики звена, а также о быстроте ее затухания. Степенью затухания ψ называют величину, равную отношению разности двух соседних амплитуд переходного процесса к первой из них (рис. 2.8а)
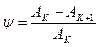 (2. 13)
(2. 13)
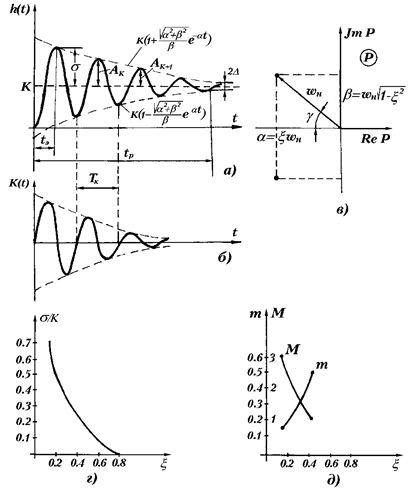
Рис. 2.8. Колебательное звено:
а - переходная функция; б - функция веса; в - распределение корней в комплексной плоскости; г - зависимость перерегулирования σ от относительного коэффициента демпфирования ξ; д - зависимость коэффициента m и показателя колебательности М от относительного коэффициента демпфирования ξ
Чем больше ψ, тем быстрее происходит затухание переходного процесса. При ψ=0 имеем автоколебательный процесс, а при ψ =1 - AK+1=0. Для колебательного звена имеется связь ψ с m
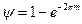 , (2. 15)
, (2. 15)
б) Относительная резонансная частота ир , максимум амплитудной частотной характеристики А(ир), показатель колебательности М
При 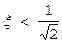 АЧХ колебательного звена заведомо имеет максимум, который определяется выражением:
АЧХ колебательного звена заведомо имеет максимум, который определяется выражением:
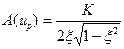 , (2. 17)
, (2. 17)
где ир - относительная резонансная частота, при которой имеем максимум АЧХ, определяется выражением:
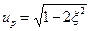 (2. 18)
(2. 18)
Зная ир, просто находим резонансную частоту:
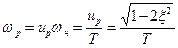 (2. 19)
(2. 19)
Наконец, так как А(0) для колебательного звена равно К, то выражение для показателя колебательности М , равное отношению A(ир)/A(0), примет вид:
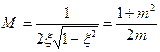 (2. 20)
(2. 20)
График зависимости М от ξ дан на рис. 2.8д.
Исходным выражением при расчете АСР на заданную степень затухания (заданные запасы по модулю и фазе) является уравнение АСР для расширенных АФХ, аналогичное характеристическому, используемому при расчете системы на устойчивость [15]:
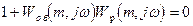 (2.102)
(2.102)
или с учетом (2.51), (2.52)
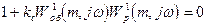 , (2.103)
, (2.103)
где Kc=KобKp - коэффициент усиления системы, а W1об(m,jω) и W1p(m,jω) - расширенные АФХ, соответственно, объекта и регулятора при единичных коэффициентах передачи Kоб и Kp.
Наряду с кривыми Д-разбиения по коэффициенту усиления системы, выражение для которых, получаемое из характеристического уравнения системы, имеет вид
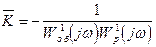 , (2.104)
, (2.104)
где черта над 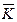 обозначает, что кривая Д-разбиения является комплексной характеристикой, а W1об(m,jω) и W1p(m,jω) - соответственно, АФХ объекта и регулятора при единичных коэффициентах передачи Kоб и Kp, введем понятие суженных кривых Д-разбиения, которые будем помечать дополнительной чертой над комплексным параметром
обозначает, что кривая Д-разбиения является комплексной характеристикой, а W1об(m,jω) и W1p(m,jω) - соответственно, АФХ объекта и регулятора при единичных коэффициентах передачи Kоб и Kp, введем понятие суженных кривых Д-разбиения, которые будем помечать дополнительной чертой над комплексным параметром 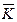 .
.
При этом суженные кривые Д-разбиения (кривые Д-разбиения с заданной степенью затухания) по коэффициенту усиления системы получаем из (2.103):
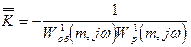 (2.105)
(2.105)
Рассмотрим графическую интерпретацию выражений (2.104) и (2.105) для системы с ПД-регулятором и статическим объектом общего вида с запаздыванием, структура которой представлена на рис. 2.28.

Рис. 2.28. Структурная схема АСР с ПД-регулятором и объектом общего вида
Для данного случая выражения (2.104) и (2.105) запишем в виде:
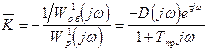 (2.106)
(2.106)
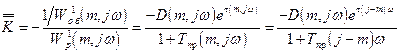 (2.107)
(2.107)
На рис. 2.29 представлена графическая интерпретация как отдельно числителя (объекта) и знаменателя (регулятора) выражений (2.106) и (2.107), так и результирующие кривые Д-разбиения по 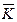 (рис. 2.29а) и
(рис. 2.29а) и 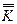 (рис. 2.29б). Кривые
(рис. 2.29б). Кривые 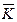 и
и 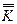 на рис.2.29 показаны для случая оптимальной настройки регулятора, соответственно по критерию Kкр (рис. 2.29а) и Kc (рис. 2.29б). Доказательство справедливости этого утверждения дано в следующем параграфе.
на рис.2.29 показаны для случая оптимальной настройки регулятора, соответственно по критерию Kкр (рис. 2.29а) и Kc (рис. 2.29б). Доказательство справедливости этого утверждения дано в следующем параграфе.
Для возможности выявления отличий в расчетах по принятым критериям, кривые рис. 2.29б показаны пунктиром на рис. 2.29а.
В дальнейшем верхний индекс 1 будем опускать, помня, однако, что при рассмотрении 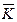 и
и 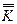 речь идет о характеристиках объекта и регулятора при единичных коэффициентах передачи (усиления), т.е. об их нормированных характеристиках.
речь идет о характеристиках объекта и регулятора при единичных коэффициентах передачи (усиления), т.е. об их нормированных характеристиках.
Для типовых промышленных регуляторов выполнение критерия 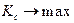 будет соответствовать условиям аналогичным (2.100), обеспечивающим минимум ранее рассмотренных в п.п. 1-5 показателям, при наличии ограничений на ψ или c и φ, т.е. для:
будет соответствовать условиям аналогичным (2.100), обеспечивающим минимум ранее рассмотренных в п.п. 1-5 показателям, при наличии ограничений на ψ или c и φ, т.е. для:
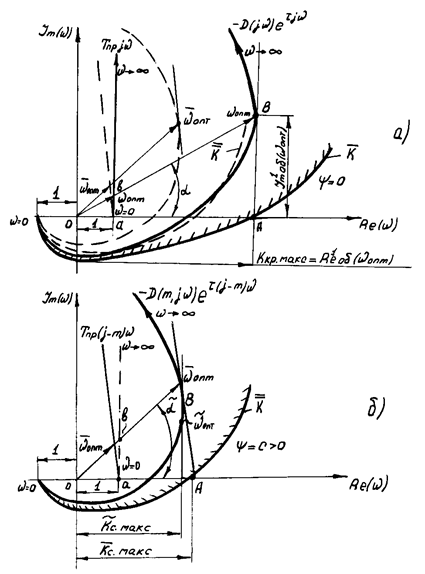
Рис. 2.29. Графическая интерпретация кривых Д-разбиения по 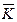 (а) и
(а) и 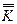 (б)
(б)
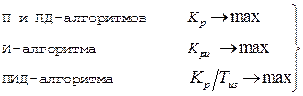 (2.108)
(2.108)
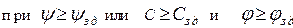 (2.109)
(2.109)
Из суженных кривых Д-разбиения по 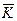 эти условия определяются сразу. Так для ПД-регулятора (рис. 2.27б) максимальное значение коэффициента передачи регулятора при ограничениях (2.109) определяется из выражения
эти условия определяются сразу. Так для ПД-регулятора (рис. 2.27б) максимальное значение коэффициента передачи регулятора при ограничениях (2.109) определяется из выражения
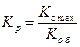 (2.110)
(2.110)
Из обычных кривых Д-разбиения по 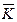 , где выделяется возможный диапазон изменения коэффициента усиления системы в виде отрезка действительной оси от начала координат, до ее пересечения с кривой
, где выделяется возможный диапазон изменения коэффициента усиления системы в виде отрезка действительной оси от начала координат, до ее пересечения с кривой 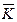 , для нахождения Kp необходимо ввести, например, запас устойчивости по модулю, тогда (см. (2.40))
, для нахождения Kp необходимо ввести, например, запас устойчивости по модулю, тогда (см. (2.40))
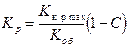 (2.111)
(2.111)
Для АСР с рядом объектов, как будет показано ниже, оптимальные настройки регуляторов, рассчитанные по критериям Kc и Kкр, могут совпадать. Это позволяет использовать для их расчета лишь критерий Kкр и, следовательно, исключить получение расширенных АФХ (суженных кривых Д-разбиения), что существенно позволит упростить расчет оптимальных настроек регуляторов.
Расчет по расширенным АФХ.
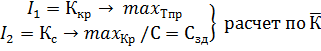
Расширенная АФХ:
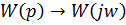 ,
,
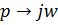 .
.
Для расширенной частотной характеристики:
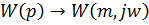 ,
,
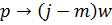 ,
,
где m - коэффициент колебательности.
Гипотеза об эквивалентности: поведение колебательного звена и поведение замкнутой системы.
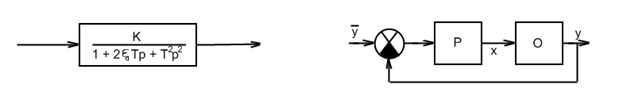


Гипотеза не всегда выполняется.
Смысл гипотезы в том, что колебательное звено и замкнутая система ведут себя одинаково (схоже), следовательно можно имея колебательное звено предполагать о наличии замкнутой системы.
У колебательного звена однозначная связь между прямыми и косвенными показателями качества.
| Прямые показатели качества | Косвенные показатели качества |
| δ, tp, σ, y1max, d,ψ | m, M, c, φ, ∫ |
Переходим на суженые кривые для того чтобы обеспечить показатели с, φ.
