Перевірка резистора на лінійність

Дослідження резистивних елементів на предмет їх

лінійності та ідеальності (безінерційності)

Теоретичне дослідження

Згідно з положеннями діалектичного матеріалізму (світогляду) та сучасної теорії систем, об’єкти реального світу (в нашому випадку електротехнічні об’єкти (ЕТО)) не можуть бути абсолютно лінійними, автономними (ізольованими від оточуючого простору), стаціонарними (в природі не існує фізичних констант). Дійсно, всі об’єкти реального світу матеріальні, а матерія і рух нерозривні. Внаслідок закону загального взаємного зв’язку вони безпосередньо чи опосередньо зв’язані між собою. Останнє призводить до їх постійного руху. Як відомо з теорії стійкості динамічних систем, внаслідок їх нескінченномірності і взаємнозв’язаності, залежність швидкості 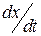і координат 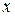навіть при розгляді її в нескінченно малій області, як лінійної

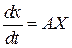
(стійкість у малому), буде мати характеристичний поліном з нульовим або навіть додатними коренями .

Тому актуальною задачею є визначення в яких часових інтервалах і динамічному діапазоні змінних ЕТО і з якою похибкою його можна подавати лінійно стаціонарною математичною моделлю кінцевої розмірності. Як відомо з електротехніки, більшість резисторів прийнято вважати ідеальними (лінійними, стаціонарними, безінерційними). Ідеальний резистор повинен мати активний опір 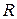, на якому згідно до закону Джоуля–Ленца електрична енергія 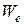за час 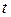повністю і безповоротно перетворюється в теплову :

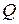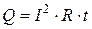. (1)

Теплова енергія витрачається на нагрів резистора. Щоб визначити як впливає температура 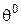резистора на його опір 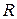достатньо скористатися фізико-математичною моделлю опору :

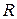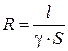, (2)

де 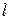– довжина, 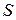– площа поперечного перерізу, 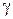– питома провідність провідника резистора.

Як відомо із курсу фізики:

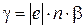, (3)

де 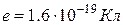– заряд електрона, 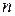– концентрація вільних електронів у провіднику, 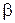– коефіцієнт вільного пробігу електрону, який для металів зменшується при збільшенні температури 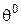внаслідок збільшення протидії напрямленому руху тепловим хаотичним, для напівпровідників навпаки – збільшується. Тобто

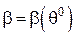. (4)

Тоді опір 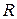буде функцією 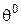. Для відносно малих змін 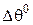ця залежність майже лінійна:

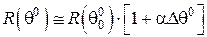, (5)

де 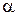- температурний коефіцієнт опору.

Як відомо з термодинаміки, для малих приростів 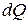теплоти 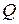має місце диференціал:

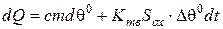, (6)

де 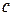– теплоємність, 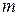– маса, 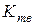– коефіцієнт тепловіддачі, 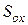– площа охолодженого резистора.

Швидкість зміни 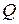є потужність 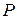, яку отримаємо, якщо продиференціювати вираз (6):

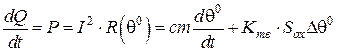. (7)

Якщо для спрощення прийняти, що потужність 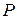незмінна, то в усталеному режимі 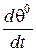дорівнюватиме нулю, а

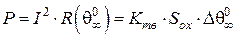, (8)

де .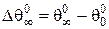

Тоді рівняння (7) набуває вигляду:

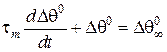, (9)

де 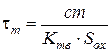– теплова стала часу резистора, , .

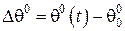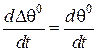Для потужних резисторів, реостатів стала часуможе бути значною. Нагрів провідника резистора згідно (9) відбувається за експоненціальним законом (рис. 1):

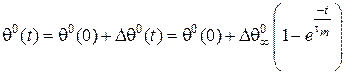. (10)

Відповідно 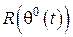, з урахуванням (5) і (10), буде змінюватись у часі, змінюючи за тією ж експонентою свій опір від 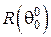до 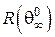(рис. 2):

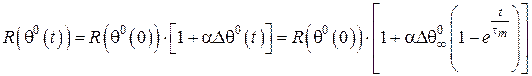. (11)

При підключенні резистора до ідеального джерела постійної напруги 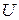струм у колі «джерело – резистор» за законом Ома з урахуванням залежності (11) буде зменшуватись у часі приблизно за тим же експоненціальним законом (рис.3):

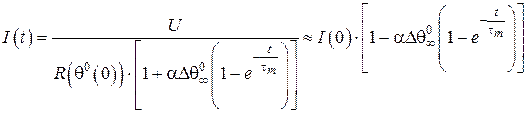. (12)

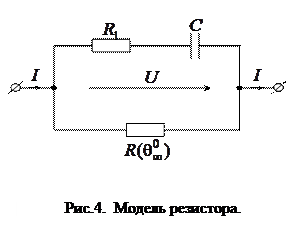
Графіку 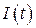(рис.3) відповідає схема заміщення реального резистора (рис.4), як - двополюсника:

В момент комутації ємнісний опір нульовий. Тому

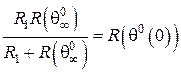. (13)

Звідки

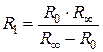, (14)

Ємність 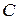визначаємо з умови 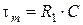з урахуванням (11) і (9):

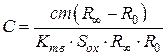. (15)

Залежно від динаміки зміни напруги 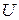, коефіцієнтів 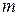, , 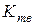, , 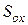, 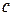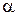приросту 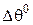залежність 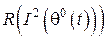може бути як суттєвою ,так і несуттєвою.

Відповідно резистор може розглядатися як безінерційний, так і інерційний, як лінійний елемент зі сталим опором 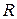, так і нелінійний, де .

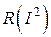Повернемося до усталеного режиму ( 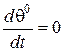) і визначимо аналітичну залежність 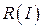. З рівняння (7) при 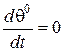і 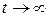маємо:

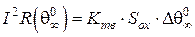. (16)

Найдемо звідси 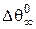і підставимо в рівняння (5):

,

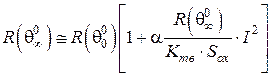або

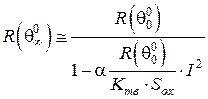. (17)

Враховуючи, що 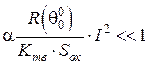з розкладання (17) в ряд замість (17) маємо наближено:

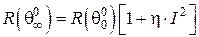, (18)

де 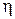- параметр резистора, який визначає вплив струму І на опір R,

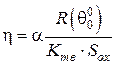. (19)

Параметр 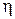пропорційний 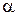і зворотно пропорційний 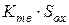. Залежно від величини 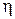і 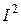, а також точності вимірювань, резистор слід розглядати як лінійний чи нелінійний елемент.

В експерименті при його детальному плануванні слід розглядати дві цілі:

1) Для існуючих приладів перевірити чи будуть резистори лінійними (опір 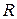незмінним) з урахуванням точності вимірювання напруги 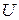і струму .

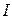2) Шляхом оптимального планування експерименту (значень 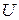, 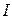і кількості їх вимірювань) все таки визначити цей малий параметр .

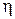Для визначення першої цілі (перевірки чи можна вважати резистори стенду лінійними елементами, в межах похибок вимірювальних приладів стенду) – проведемо планування експерименту з вибором оптимального варіанту. Стенд має стрілочні амперметри з рівномірною шкалою від 0 до 5 А та класом точності 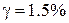; цифровий мультиметр виміру напруги або опору з абсолютною похибкою – одиницею молодшого десяткового розряду, тобто 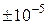. Визначення опору 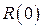холодного резистора можна досить точно виміряти омметром. Струм омметра практично не змінить температуру резистора внаслідок його малості. Опір нагрітого резистора визначимо методом вольтметра-амперметра для максимально допустимого струму 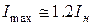, де 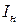– номінальне значення. Резистори мають паспортні данні 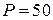Вт, 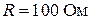, тоді .

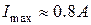Для зменшення систематичної похибки, пов’язаної з ненульовим опором амперметра, вимірюємо його опір за допомогою омметра. Тоді незміщена оцінка 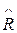опору резистора 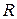дорівнюватиме:

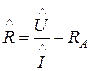, (20)

де 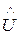, 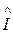– виміри цифровим вольтметром напруги джерела 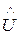, аналоговим амперметром струму 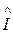і 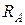- вимір опору амперметра (маючи велику точність омметра можна вважати точним).

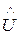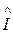Виміри і мають випадкові помилки, які некорельовані як між собою, так і між вимірами і, як правило, мають нормальний гаусовий розподіл.

Абсолютну похибку амперметра визначимо за його класом точності ( )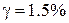

.

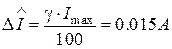Абсолютна похибка вимірювання напруги пов’язана не стільки з вольтметром (він досить точний), як з нестабільністю напруги джерела 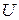. Для оцінювання нестабільності виконаємо 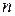вимірювань 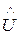, знайдемо оцінку середнього значення:

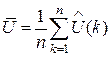, (21)

і незміщену оцінку 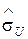середньоквадратичного розкиду 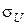вимірів 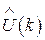відносно :

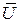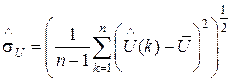, (22)

яку приймемо за похибку : .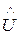

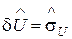Оцінку нагрітого резистора при 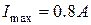отримаємо за формулою (20), де в якості 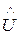візьмемо 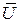(21). Висновок про лінійність чи не лінійність резистора з відповідною достовірністю можна зробити шляхом співставлення 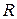холодного резистора (вимір омметром) і 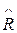як відношення 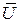до 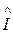. Вважаючи похибку 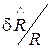досить малою, маємо:

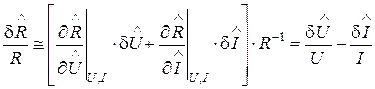. (23)

Похибки 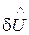і 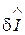по своїй суті мають випадковий характер. Це, як правило, нормальний розподіл з нульовим математичним очікуванням і дисперсіями 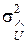, 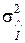. В результаті n спостережень напруги U (наприклад 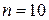)маємо вибірку 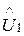, , 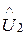…, 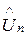об’єму 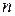. В процесі виміру 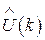, 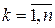показ стрілочного амперметра 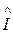, внаслідок його інерційності і грубості, майже не змінюється. Таким чином незміщена оцінка 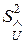дисперсії 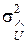визначається з експерименту

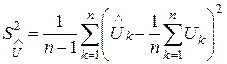, (24)

а оцінка 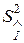дисперсії 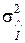визначається через клас точності 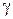амперметра, як квадрат абсолютної похибки:

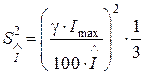. (25)

Враховуючи взаємну некорельованість випадкових помилок 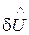і 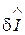, та їх малість відносно 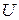і 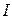, з урахуванням (23), отримаємо оцінку 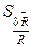кореня з дисперсії :

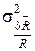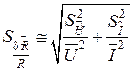, (26)

де 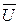, 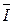– середні значення напруги і струму за 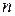дослідів.

Результат вимірювання опору 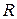холодного резистора цифровим омметром з точністю до п’яти десяткових розрядів можна прийняти за точне значення 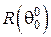, оскільки струм омметра надто малий.

Результати вимірювання (20) опору 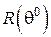резистора, нагрітого струмом 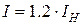, мають середнє значення

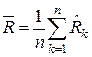(27)

і оцінку дисперсії

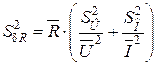. (28)

Для прийняття рішення щодо неістотності зміни опору від струму ( 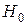гіпотеза), чи істотності ( 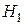гіпотеза) побудуємо випадкову величину :

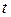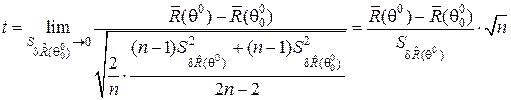. (29)

Величина 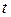за умови правильності гіпотези 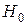має розподіл Стьюдента з 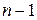степенями свободи. Двостороння критична область симетрична відносно нуля і знаходиться за умови, що ймовірність прийняття гіпотези 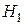дорівнює взятому рівню значущості 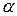, коли правильна гіпотеза 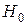( 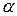– похибка першого роду).

Критична точка 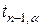знаходиться за таблицею розподілу Стьюдента для кількості степенів свободи 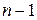і ймовірності

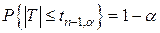. (30)

Якщо 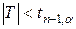, то приймається гіпотеза 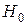, а якщо 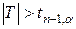, — то гіпотеза .

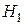У лабораторній роботі №1 перевіримо 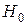гіпотезу для опору резистора і опору лампи розжарювання при зміні струму від мінімального до струму 120 % від номінального.

Приклад.

Перевірка резистора на лінійність

Точний показ омметра: 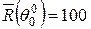Ом.

Десять результатів вимірювання напруги , .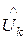

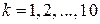Таблиця 1

k
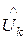, В	80,4	79,5	80,5	79,8	81,01				80,5
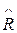,Ом	100,5	99,37	100,5	99,75	101,3	97,5	102,5		100,6	98,75

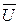=80,07 В, 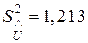В², 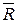=100,09 Ом;

оцінка (25) ;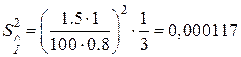

оцінка(28) ;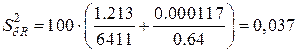

величина (29) ;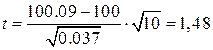

кількість степенів свободи 9; похибка першого роду 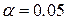; критичне значення (за таблицями t-критерій Стьюдента) .

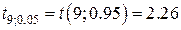Оскільки 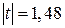менше 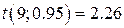, то можна вважати, що нуль-гіпотеза справедлива.