Багатоканальні С.М.О. із необмеженою чергою

Розглянемо випадок, коли довжина черги в С.М.О. не обмежена числом m, а може бути як завгодно велика, тобто 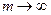. Граф станів у цьому випадку безкінечний, мал.12:

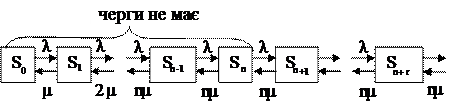мал. 12.

Так як ймовірності станів знаходилися за формулами (2.52 – 2.54), то для визначення можливостей станів у даному випадку їх можна використовувати прагнучи 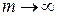. Так як сума геометричної прогресії 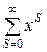сходиться (формула для Р₀) при x=α /n<1 і розходиться при x≥ 1, то сталий режим буде існувати при x<1, а при x≥ 1 черга буде нескінченно зростати. Нехай x=α /n<1. Тоді ймовірності станів такі ж, що й у (53-54):

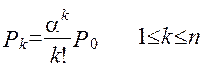(2.66)

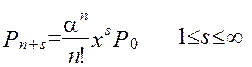(2.67)

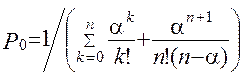(2.68)

Так як заявка буде рано чи пізно обслуговувана, то характеристики пропускної спроможності С.М.О.:

P_відм= 0; q=1; А=λ_*q= λ .

Середнє число заявок у черзі одержимо при 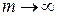. З (2.62)

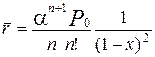(2.69)

Середній час чекання з (3.40)

T_оч= 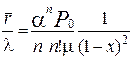(2.70)

Середнє число зайнятих каналів

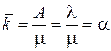(2.71)

Середнє число заявок у С.М.О.

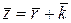(2.72)

Приклад 10. Автозаправочна станція (АЗС) з двома колонками (n=2), найпростіший потік машин інтенсивності λ=0,8 машин/год. Середній час обслуговування однієї машини t_об=2 хв. У даному районі немає іншої АЗС, так що черга машин перед АЗС може рости практично необмежено. Знайти характеристики С.М.О.

Рішення. Маємо λ=0,8; μ=0,5; n=2; α=1,6; x=α/n=1,6/2=0,8.

Так як x<1, то черга не зростає нескінченно і існує граничний стаціонарний режим роботи С.М.О.

По формулах (66-68) знаходимо ймовірності станів:

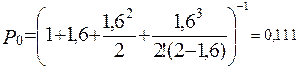
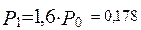
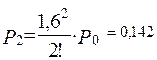
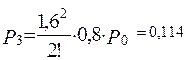
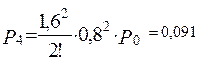
Середнє число зайнятих каналів 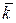=А/μ =λ /μ=α =1,3.

Ймовірність відсутності черги в АЗС P₀+P₁+P₂=0,111+0,178+0,142=0,431.

Середнє число машин у черзі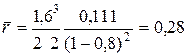

Середнє число машин на АЗС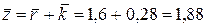

Середній час чекання в черзі T_оч = 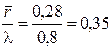хв.

Середній час перебування машини на АЗС 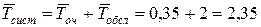хв.

ТЕОРІЯ ІГОР

В житті часто виникають конфліктні ситуації, що характеризуються наявністю протилежних інтересів і спрямувань окремих людей і колективів, що намагаються досягнути своїх цілей часто із шкодою один до іншого. Математичним моделюванням умов конфлікту і пошуком на цій основі оптимальних рішень займається теорія ігор. Теорія ігор дає рекомендації з раціонального образу дій кожного з учасників в ході конфліктної ситуації, тобто таких дій, які забезпечували б йому найбільший виграш (найменший програш).

Ігрової схеми можна надати багатьом ситуаціям в економіці. Тут виграш - це ефективність використання дефіцитних ресурсів, виробничих фондів, величини прибутку і т. і.

Приклад 1. Виконується проектування дільниці по обробці заготовок. Заготовки можуть виконуватись з різних матеріалів і оброблятись на різних верстатах. В табл.1 наведено вартість обробки однієї заготовки в залежності від матеріалу і типу верстатів, на яких ведеться обробка.

Табл.1.

Тип верстата	Вид матеріалу
М1	М2	М3	М4
S1	6,20	6,70	6,30	6,70
S2	6,30	6,50	6,55	6,50
S3	6,10	6,40	6,40	6,60
S4	5,80	6,35	6,80	6,40

Зрозуміло, що замовник (володар заготовок) прагне вибрати матеріал таким чином, щоб вартість однієї заготовки була мінімальною. З іншого боку, обробник деталей прагне так сформувати парк верстатів для обробки деталей, щоб отримати найбільший прибуток. Має місце конфліктна ситуація, і треба дати рекомендації кожній із сторін щодо їх оптимальної поведінки.