Короткі теоретичні відомості. Теорія електричних та магнітних кіл
Теорія електричних та магнітних кіл
Методичні вказівки
до лабораторних робіт
для студентів спеціальності 8.091.501
“Комп’ютерні системи та мережі”
всіх форм навчання
Методичні вказівки до лабораторних робіт з дисципліни “Теорія електричних та магнітних кіл”, „Сигнали та процеси в радіотехніці”, „Основи теорії кіл” для студентів спеціальності 8.091501, 8.090701, 8.090503 всіх форм навчання. (Укл. Т.І. Бугрова. – Запоріжжя: ЗНТУ, 2004, - 38 с.)
Укладач: Т.І. Бугрова, ст. викладач
Рецензент: М.М. Касьян, к.т.н. ст. викладач
Відповідальний за випуск: Т.І. Бугрова, ст. викладач
Затверджено на засіданні кафедри
„Радіотехніки”
Протокол №1 від 27 серпня 2001р.
Перелік скорочень
АМ – амплiтудна модуляцiя
АЧХ - амплiтудно-частотна характеристика
ГВЧ – генератор високих частот
ГНЧ – генератор низьких частот
IХ – iмпульсна характеристика
КЧХ – комплексна частотна характеристика
ЛЦФ - лiнiйний цифровий фiльтр
ТЕМК – теорiя електричних та магнiтних кiл
ФЧХ – фазо-частотна характеристика
ЗМІСТ
ПЕРЕЛІК СКОРОЧЕНЬ 3
ВСТУП 5
1 ЛАБОРАТОРНА РОБОТА №1. АНАЛІЗ І СИНТЕЗ СИГНАЛІВ
ПО ХААРУ 6
2 ЛАБОРАТОРНА РОБОТА №2. АНАЛІЗ І СИНТЕЗ СИГНАЛІВ
ПО ФУР’Є 11
3 ЛАБОРАТОРНА РОБОТА №3. АНАЛІЗ І СИНТЕЗ ЛІНІЙНИХ ЦИФРОВИХ ФІЛЬТРІВ 14
4 ЛАБОРАТОРНА РОБОТА №4. НЕЛІНІЙНЕ РЕЗОНАНСНЕ ПІДСИЛЕННЯ ТА МНОЖЕННЯ ЧАСТОТИ 27
ЛАБОРАТОРНА РОБОТА №5. АМПЛІТУДНА МОДУЛЯЦІЯ
ЗМІЩЕННЯМ 34
ПЕРЕЛІК ПОСИЛАНЬ 38
ВСТУП
Дисципліна ТЕМК є базовою у підготовці інженера-системотехніка. Його фахова діяльність вимагає глибоких знань у галузі комп’ютерної техніки, техніки передавання, відображення та відбору інформації. Всі технічні засоби, що застосовуються у цих галузях, мають загальну основу - електронні блоки, функціювання яких визначається рухом носіїв електричних зарядів.
Законами електричних кіл користуються для розрахунків схем окремих інтегральних вузлів, блоків комп’ютерів й систем керування.
Метою лабораторного курса є здобуття практичних навичок застосування законів електричних кіл для моделювання фізичних процесів, що відбуваються при перетворенні інформації у вигляді сукупності електричних сигналів, а також вироблення навиків експериментального дослідження елементів складних систем та пристроїв.
1 ЛАБОРАТОРНА РОБОТА №1. АНАЛІЗ І СИНТЕЗ СИГНАЛІВ ПО ХААРУ
Мета роботи – вивчення можливості апроксимації сигналу багаточленом Фур’є по ортогональній системі функцій Хаара.
Синтезуються сигнали різноманітної форми та досліджується вплив кількості ортогональних складових на похибку апроксимації.
Короткі теоретичні відомості
Систему ортонормальних функцій Хаара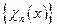 
можна використовувати в якості базисної при розвиненні у ряд Фур’є - Хаара, що рівномірно збігається неперервної на відрізку [0, 1], будь – якої функції
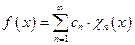
з коефіцієнтами
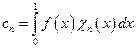
При використанні функцій Хаара в якості базисних для апроксимації сигналів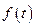 
на відрізку 
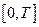багаточленами Фур’є безрозмірний аргумент 
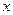функції Хаара необхідно замінити на 
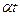, де коефіцієнт 
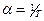завдає необхідний масштаб часу функцій і має розмірність часу у мінус першому ступені.
В означенні функцій Хаара використовується поняття двоїчних відрізків. Відрізки, які можна отримати розподілом відрізку [0, 1] на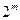 
рівних частин, називаються двоїчними. Ці відрізки вважають замкненими зліва і відкритими праворуч, якщо їх правий кінець не дорівнює одиниці. Якщо правий кінець відрізка дорівнює одиниці, то відріізок вважають замкненим і зліва, і справа. Такам чином, двоїчні відрізки – [0,1], [0,1/2[, [1/2,1], [0,1/4[, [1/4,1/2[, [1/2,3/4[, [3/4,1], [0,1/8[ . Відрізки [1/4, ¾[, або [5/8, 7/8[ не є двоїчними.
Для двоїчних відрізків введемо наступні позначення:
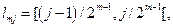
де j міняється від 1 до 2m-1 , а m=1,2,... (коли j=2m-1 треба вважати lmj замкненим також і праворуч)
Для кожного m виконується умова lm1+lm2+lm3+...+lm2m-1=[0,1[.
Разом із подвійною нумерацією використовують просту нумерацію, вважаючи lmj=ln , де n=2m-1+j . Насправді, при такій нумерації т=2,3,... (відрізок з n=1 відсутній). Ліву і праву половину lmj домовимось позначати lmj- і lmj+, так що
.
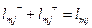Систему функцій Хаара 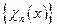зручно будувати групами: група номер m містить 2m-1 функцій 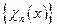, j=1,2,...2m-1, m=1,2,3..., причому перша функція 
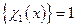залишається поза групами.
Означення функцій Хаара
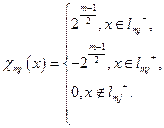
На рис.1.1 зображені перші вісім функцій цієї системи.
 |
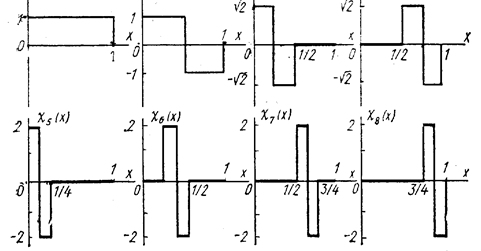Особливість функцій Хаара – порівняна простота їх отримання (генерування у електронних пристроях). Базисну систему функцій Хаара доцільно використовувати для аналізу та синтезу імпульсних сигналів кінцевої тривалості.
Рис.1.1