Современные методы кодирования

К наиболее эффективным методам обеспечения высокого качества цифровой передачи в условиях высокого уровня шума канала связи относятся весьма мощные алгоритмы формирования корректирующих кодов, в разработке которых теория помехоустойчивого кодирования имеет значительные успехи.

За годы развития в технику связи успешно внедрены пороговые декодеры, алгоритм Витерби, коды Рида-Соломона, каскадные схемы кодирования, а также разработки последнего времени – алгоритмы для турбо кодов, многопороговые декодеры и каскадные методы кодирования и декодирования.

Однако требования к алгоритмам коррекции ошибок в каналах связи с помехами, в частности в спутниковых каналах, непрерывно растут и главная проблема – декодирование с эффективностью, близкой к оптимальной по энергетике канала, но при максимально простой реализации.

Основными характеристиками методов коррекции ошибок являются:

- средняя вероятность ошибки в информационном бите или последовательности бит;

- энергетический выигрыш кодирования (ЭВК), показывающий величину снижения энергии, необходимой для передачи одного бита данных при некоторой выбранной средней вероятности ошибки;

- сложность реализации алгоритма как программной так и аппаратной. Данная характеристика имеет большое значение, так как применяя очень сложные методы кодирования, получают высокий ЭВК, но эти методы практического применения не находят.

На сегодняшний день известно множество различных классов помехоустойчивых кодов, отличающихся друг от друга структурой, функциональным назначением, энергетической эффективностью, алгоритмами кодирования и декодирования и многими другими параметрами. На рисунке 2.2 представлена классификация помехоустойчивых кодов.

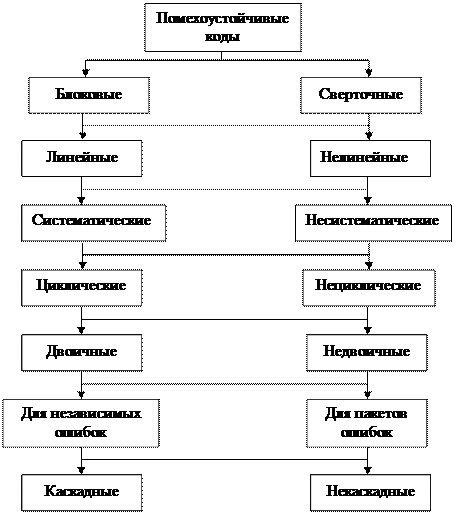
Рисунок 2.2 – Классификация помехоустойчивых кодов

К основным наиболее распространенным кодам можно отнести:

1) блоковые коды, в которых кодирование и декодирование производится в пределах кодовой комбинации или блока. К ним относят коды Боуза-Чоудхури-Хоквингема, коды Рида-Соломона, мажоритарно декодируемые коды;

2) сверточные коды, в которых обработка символов производится непрерывно, без разделения на блоки;

3) линейные коды, образующие векторное пространство и обладающие важным свойством: два кодовых сообщения можно сложить, используя подходящее определение суммы, и получить третье кодовое слово. Данное свойство упрощает процедуру кодирования и декодирования. Важный подкласс линейных кодов составляют циклические коды или CRC коды (Cyclic Redundancy Codes – Циклические Избыточные Коды);

4) каскадные схемы кодирования, в основе построения которых лежит идея совместного использования нескольких составляющих кодов. Данный подход позволил существенно повысить эффективность применения кодирования по сравнению с базовыми некаскадными методами. Примером могут служить каскадные коды, построенные с использованием кода Хемминга и его модификации, особое место среди кодовых схем занимают каскадирование с кодами контроля по четности, а также каскадные схемы с методами параллельного кодирования, образуя турбо коды, которые формируются при параллельном каскадировании двух или более составляющих кодов.

Задачи по разделу 2

Пример 1.Приняты две кодовые комбинации 0001 и 1111. Определить значность кодовых комбинаций, их вес и кодовое расстояние между комбинациями.

Решение:

1) определение значности соответствует количеству разрядов – n в кодовой комбинации: n₁=n₂=4.

2) определение веса по количеству «1» в комбинации: V₁=1;V₂=4.

3) кодовое расстояние между комбинациями – определяется как вес суммы по модулю два кодовых комбинаций: 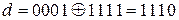; d=3.

Пример 2. Принята кодовая комбинация 101011. известно, что вектор ошибки 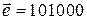. Найти исходную кодовую комбинацию.

Решение:

Для нахождения кодовой комбинации определим сумму по модулю два для принятой комбинации и вектора ошибки: ; ; ;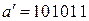

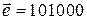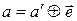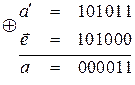
Пример 3. Передана кодовая комбинация 1100. Известно, что вес 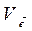вектора ошибки равен 2. Найти:

1) возможные варианты искаженных комбинаций.

2) кодовое расстояние, необходимое для обнаружения и устранения всех ошибок.

Решение:

1. Возможные варианты комбинаций состоят из тех комбинаций, которые отличаются от исходной двумя позиционными местами, т.к. .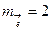

Возможные варианты:1010, 1001, 0110, 0101, 0000.

Проверим комбинации, сложив их по модулю два с исходной комбинацией: .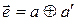

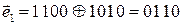
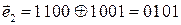
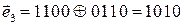
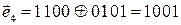
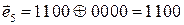
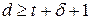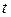2. Для обнаружения и исправления всех ошибок необходимо, чтобы кодовое расстояние , где – обнаруживаемые ошибки; 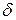– исправляемые ошибки. При разрядности нашего числа 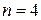могут возникнуть четырехкратные ошибки.

Следовательно, для их исправления и обнаружения необходимо, чтобы кодовое расстояние удовлетворило условию: 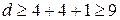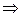необходимо увеличить разрядность кода.

Пример 4. Определить корректирующую способность кода, имеющего следующие разрешенные комбинации: 00000, 01110, 10101, 11011.

Решение:

Построим таблицу и определим кодовые расстояния между комбинациями.

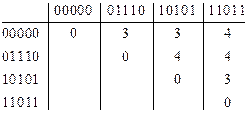
Кодовое расстояние 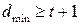; ; 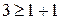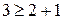. Следовательно, код обнаруживает двукратные и однократные ошибки.

Устраняет однократные ошибки , т.к. 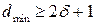; при 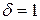, 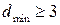; 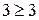. При кодовом расстоянии 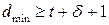код исправляет ошибки.

При 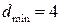, , 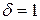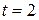код исправляет одиночные и двукратные ошибки.

Пример 5. Определить значность кода n, обеспечивающего исправление всех однократных ошибок при количестве разрешенных комбинаций N=8.

Решение:

1) Определим значность кода по формуле: .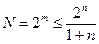

2) Определим количество информационных символов- m:

;

; .

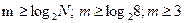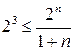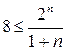При 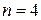т.к. m<n условие 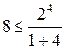не выполняется;

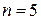условие 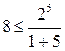не выполняется;

n=6 условие 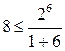выполняется.

Следовательно, значность кода n=6.

Пример 6. Заданы кодовые комбинации: 0010, 11011. Образовать для этих комбинаций коды с четным и нечетным числом единиц, код с удвоением элементов и инверсный код.

Решение:

1) Код с четным числом единиц:

0010 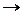10010;

11011 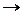011011.

2) Код с нечетным числом единиц:

0010 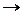00010;

11011 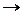111011.

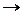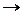3) Код с удвоением элементов: 1 10; 0 01.

0010 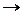01 01 10 01;

11011 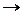10 10 01 10 10.

4) Инверсный код:

0010 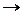00101101;

11011 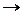1101111011.

Пример 7. Для кодовых комбинаций определить код Хемминга.

Решение:

1) исходная комбинация 10011.

Представим информационные и проверочные разряды: для комбинации 10011 m=5, разрядность кода n=9. Для 9-и разрядного кода символы а₁, а₂, а₄ и а₈ – проверочные (контрольные), остальные – информационные.

а₉ а₈ а₇ а₆ а₅ а₄ а₃ а₂ а₁

И П И И И П И П П

1 1 0 0 1 1 1 1 1

Находим значение проверочных символов из выражения:

; ;

; ;

; ;

; ;

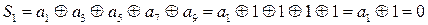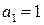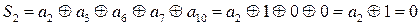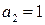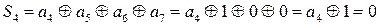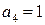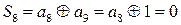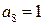Причем, S_i =0. Вписываем значение проверочных разрядов и получим комбинацию кода Хемминга: 10011 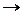110011111.

2) Исходная комбинация 111110; m=6; .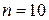

Проверочные символы: , , , .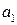

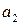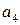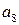Информационные символы: , , , , , .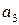

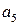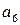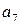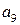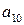а₁₀ а₉ а₈ а₇ а₆ а₅ а₄ а₃ а₂ а₁

И И П И И И П И П П

1 1 0 1 1 1 1 0 1 1

Определим проверочные символы из выражения:

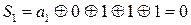
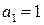
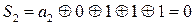
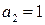
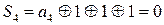
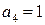
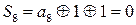
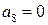
Исходная комбинация преобразуется в код Хемминга: 111110 1101111011.

Пример 8. Принята искаженная кодовая комбинация, закодированная кодом Хемминга. Определить разряд, где произошла ошибка.

1) 111110110;

2) 1101010111.

Решение:

1) исходная комбинация:

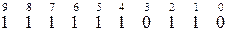
Найдем суммы S_i и определим двоичное число

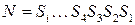
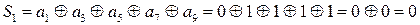
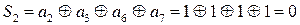
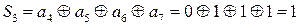
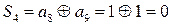
N=S₄ S₃ S₂ S₁=0100. В четвертом разряде произошла ошибка, т.е. не искаженная комбинация - 111111110.

2) исходная комбинация:

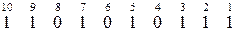
Найдем суммы S_i и определим двоичное число

;

;

;

;

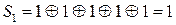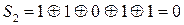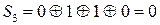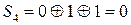N=0001 , следовательно в первом разряде произошла ошибка

Пример 9.Определить и исправить ошибку в передаваемой комбинации вида:

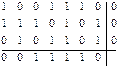
Для контроля использовать метод четности.

Решение:

Проведем проверку на четность по строкам: k₁=0; k₂=1; k₃=0; по столбцам: k₄=0; k₅=0; k₆=0; k₇=1; k₈=0; k₉=0; k₁₀=0. Проверка показала, что ошибка возникла в разряде второй строки четвертого столбца.

Запишем правильный вариант:

.
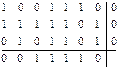