Шаг 4.Выбрать вершину ; на Шаг 5

Шаг 5.Увеличение потока.

1. Если метка вершины 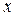имеет вид , то изменить поток вдоль дуги с на .

2. Если метка вершины 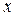имеет вид , то изменить поток вдоль дуги с на .

Шаг 6.Если , то стереть все метки и вернуться к Шагу 1.При этом используется уже увеличенный поток, найденный на Шаге 5.

Если , то положить ; на Шаг 5.

Пример. Найти максимальный поток и минимальное сечение для графа, пропускная способность каждого ребра равна 1.

3 – минимальное сечение

3 – максимальный поток

Решение.

1.Пусть исходный поток будет нулевой: .

F	с(x,y)	f0(x,y)	f1(x,y)	f2(x,y)	f3(x,y)
0 1				+
0 3						+
0 4								+
0 5										+
1 2								+
1 3				+				-
2 6									+
3 5						+
3 6				+
4 5										-
4 6						+

2. Пометим ребра 01, 13, 36 знаком + и направим по найденному маршруту поток 1.

Маршрут для потока f1(x, y)

3. Пометим ребра 03, 35, 56 знаком (+) и направим по найденному маршруту поток 1.

Маршрут для потока f2(x, y)

Полученный поток f2 (x, y) содержит по крайней мере одну насыщенную дугу – то есть является "полным" потоком.

4. Попробуем улучшить полученный поток:

1. Пометим знаком (+) узел 0.

2. Пометим знаком (+) ненасыщенные дуги 04 и 45. Так как из вершин 5 выходит насыщенная дуга 56, пометим знаком (-) ненулевой поток 35. Так как из вершины 3 выходит насыщенная дуга 36, пометим знаком (-) ненулевой дуги 13. Пометим знаком (+) ненасыщенные дуги 12, 26.

3. На вновь открытом маршруте +0.4+4.5-3.5-1.3+1.2+2.6 вычислим приращение "полного" потока равен 1.

4. Пометим ребро 05 символом (+), так как из вершины 5 выходит насыщенная дуга 56, пометим знаком (–) ненулевой поток 45. То есть все узлы сети можно разбить на два непересекающихся множества

Β = {0,4,5} и Β= {1,2,3,6}.

ЗАКЛЮЧЕНИЕ

Актуальность задачи о максимальном потоке постоянно возрастает в месте со строительством трубопроводов, новых дорог, роста пользователей Интернета и любых других сетей. По этому быстрое и точное её решение крайне необходимо во всех сферах нашей деятельности, где хоть как-то встает вопрос об перемещение чего-либо куда-либо с максимальной рациональностью.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.Нефедов В. Н., Осипова В.А. Курс дискретной математики / МАИ. М., 1992.

2.Лихтарникова Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. СПб, 1988.

3.Гиндикин С.Г. Алгебра логики в задачах. М., 1972.

4.Мамонтова Н.П. и др. Методические указания к практическим занятиям по теории сетей связи / ЛЭИС. Л., 1978.

5.Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978.

6.Уилсон Р. Введение в теорию графов. М.: Мир, 1977.

7.Социально-экономическая география зарубежного мира. – М.: Крон-пресс, 1998.

8.Зуховицкий С.И., Радчик И.А. Математические методы сетевого планирования. – М., 1965.

9.Форд Л., Фалкерсон Д. Потоки в сетях. – М.: Мир, 1966. – 276 с.

10.Матушевский В.В. Теория графов / Конспект лекций. – Томск: ТГУ, Факультет информатики, 2002.