Марковський ланцюг називається однорідним, якщо перехідні ймовірності не залежать від номера кроку. У противному випадку марковський ланцюг неоднорідний.
Розглянемо однорідний марковський ланцюг із n можливих станів S1, S2, ..., Sn. Позначимо через Pij ймовірність переходу (при i = j Ймовірність затримки в стані Si) за один крок із Si у Sj. Тоді матриця з Pij називається матрицею переходу
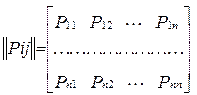 (2.1)
(2.1)
Перехідні ймовірності можна тоді уявити як умовні ймовірності Pij = = P (Sj(k)/Si(k-1))
Так як події Sj(k) утворять повну групу несумісних подій, то 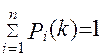 .
.
При розгляді марковських ланцюгів часто буває зручно користуватися графом станів, на якому в стрілок проставлені відповідні перехідні ймовірності, не рівні нулю (Pij¹0) і змінюючи стан системи. Такий граф називається розміченим графом станів, мал.4.
| Наприклад, для приведеного вище графа. Зауважимо, що ймовірності, що не змінюють стан системи не наводяться, тому що їх можна обчислити. | 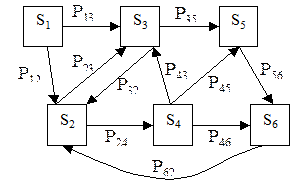 Мал. 4. Мал. 4. |
Для розглянутого прикладу Р11=1-(Р12+Р13), Р22 = 1 - (Р23 + Р24) і т. д. Якщо із стану Si не виходить жодної стрілки, тобто перехід в інший стан неможливий, то Pii=1.
Якщо є матриця переходу ||Pij|| (або розмічений граф станів) і початковий стан системи, то можна знайти ймовірності станів P1(k), P2(k), ..., Pn(k) після будь-
якого (k-го) кроку. Покажемо це.
Нехай система знаходиться в початковому стані Sm. Тоді Pi(0) = 0, крім Pm(0) = 1. Ймовірності станів після першого кроку Pi(1) = Pmi; i = 1,2, ..., n.
Знайдемо ймовірності станів після К=2; Pi(2) (i =1,2, ... ,n)
По формулі повної ймовірності з гіпотезами Sj (j=1,2, ... , n)
Pi(2) = 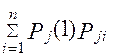 (i = 1, 2, ..., n) і т.д. Після k-го кроку
(i = 1, 2, ..., n) і т.д. Після k-го кроку
Pi(k) = 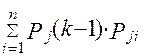 (2.2)
(2.2)
Рівняння 1 можна переписати в матричній формі
P(k) = P(k-1) × P (2.3)
де P(k), P(k-1) - вектори-рядки станів системи, Р- матриця переходу.
Приклад 4. По деякій цілі ведеться стрільба чотирма пострілами в моменти часу t1, t2, t3, t4.
Можливі стани цілі (системи S):
S1 - ціль непошкоджена;
S2 - ціль незначно ушкоджена;
S3 - ціль істотно ушкоджена;
S4 - ціль уражена цілком.
Визначити ймовірності станів цілі після чотирьох пострілів, якщо в початковий момент часу ціль знаходиться в S1, і граф станів має вид, мал.5.
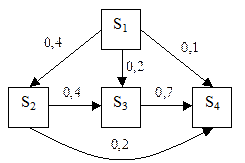 Рішення: Знайдемо матрицю переходу Р12 = 0,4; Р13 = 0,2; Р14 = 0,1 Р11 = 1 - (0,4+0,2+0,1) = 0,3 Аналогічно Р21 = 0; Р23 = 0,4; Р24 = 0,2; Р22 = 1-0,4-0,2=0,4 Р31=Р32=0; Р34=0,7; Р33 = 1-0,7=0,3 Р41=Р42=Р43=0; Р44=1 Рішення: Знайдемо матрицю переходу Р12 = 0,4; Р13 = 0,2; Р14 = 0,1 Р11 = 1 - (0,4+0,2+0,1) = 0,3 Аналогічно Р21 = 0; Р23 = 0,4; Р24 = 0,2; Р22 = 1-0,4-0,2=0,4 Р31=Р32=0; Р34=0,7; Р33 = 1-0,7=0,3 Р41=Р42=Р43=0; Р44=1 | Мал. 5 |
Тоді
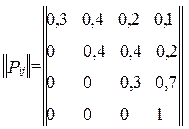
Ймовірності станів після 1-го кроку Рi(1)= P1i (i = 1,2,3,4), тобто елементи 1-го рядка матриці (початковий стан S1)
Pi(1) = (0,3; 0,4; 0,2; 0,1)
Ймовірність станів після 2-го кроку
{Pi(2)}={Pi(1)} . ||Pij|| =
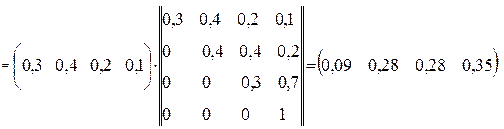
Після третього кроку ймовірність станів
{Pi(3)}={Pi(2)} ×||Pij|| 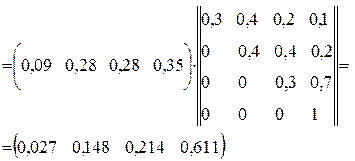
Після четвертого кроку
{Pi(4)}={Pi(3)} . ||Pij|| = 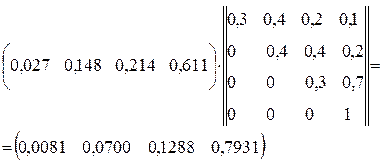
Одержали, що після чотирьох пострілів ймовірності подій P(S1) = P1(4) = 0,008; P(S2) = P2(4) = 0,07; P(S3) = P3(4) = 0,129; P(S4) = P4(4) = 0,793.
Розглянемо загальний випадок - неоднорідний марковський ланцюг, для якого ймовірності переходу Pij змінюються від кроку до кроку. Тоді ймовірність переходу буде залежати від кроку k, тобто Pij(k) = P(Si(k)/Sj(k-1). Якщо ||Pij(k)|| відомі на кожному кроку, то
{Pi(k)} = 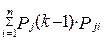 (k) = {Pj(k-1)} ||Pji(k)|| (2.4)
(k) = {Pj(k-1)} ||Pji(k)|| (2.4)
У метричній формі
P(k) = P(k-1), P(k) (2.5)
Приклад 5. Умови задачі ті ж самі, що і у попередньому прикладі. Тільки провадиться не 4, а три постріли. Причому ймовірності переходу змінюються від пострілу до пострілу.
||Pij(1)|| = ||Pij|| 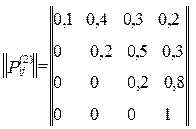
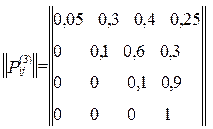
Зауваження: Матриця переходу (квадратна) Р, володіючи властивостями 0 < Pij < 1 , 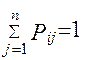 i, j = 1, ..., n у деяких джерелах називається стохастичною.
i, j = 1, ..., n у деяких джерелах називається стохастичною.
