Построение графиков функций одной переменной
Построение графиков функций одной переменной
Инструментальная панель графических окон
Построение трехмерных изображений
Построение графиков функций одной переменной
СистемаMatLabможет создавать как плоские графики, так и трехмерные сетчатые поверхности, а также движущиеся графики, или анимацию.
В научных и технических задачах основными и наиболее часто употребительными являются графики, которые представляют собой кривые, описывающие те или иные численные данные. MatLabрасполагает набором команд высокого уровня, которые используются для построения таких кривых и управления ими. Это такие команды, как plot, title, axis, text, hist, contourи ряд других. Кроме того, строить графики, управлять ими и редактировать их можно с помощью инструментальных панелей графических окон. Можно также использовать комбинацию обоих подходов. Например, можно использовать команды для создания графиков, а затем модифицировать их.
Для того чтобы построить график функции y=f(x), достаточно тем или иным способом сформировать два вектора одинаковой размерности - вектор значений аргументов x и вектор соответствующих значений функции у, а затем выполнить команду plot. Команда plotоткрывает графическое окно и отображает в нем зависимость y(x) в линейных осях, при условии что xи yявляются векторами одинаковой длины.
Рассмотрим пример построения графика синуса на интервале от -4 до 4.
| Пример 3.2-1 |
| >>x = -4:.01:4; >>y = sin(x); >>plot(x,y); >> |
В результате выполнения команд открывается графическое окно (рис. 3.2-1).
В вышеописанном примере вектор xявляется набором равноотстоящих точек с шагом 0.01, а y- вектор со значениями функции синуса в этих точках. Для отображения графика системаMatLab открывает отдельное окно с именем Figure 1. Переход между окнами, то есть возврат в окно MatLabили переход от одного графического окна к другому графическому окну осуществляется в соответствии с правилами среды: с помощью команд основного меню; комбинации <Alt+Tab>или с помощью мыши.
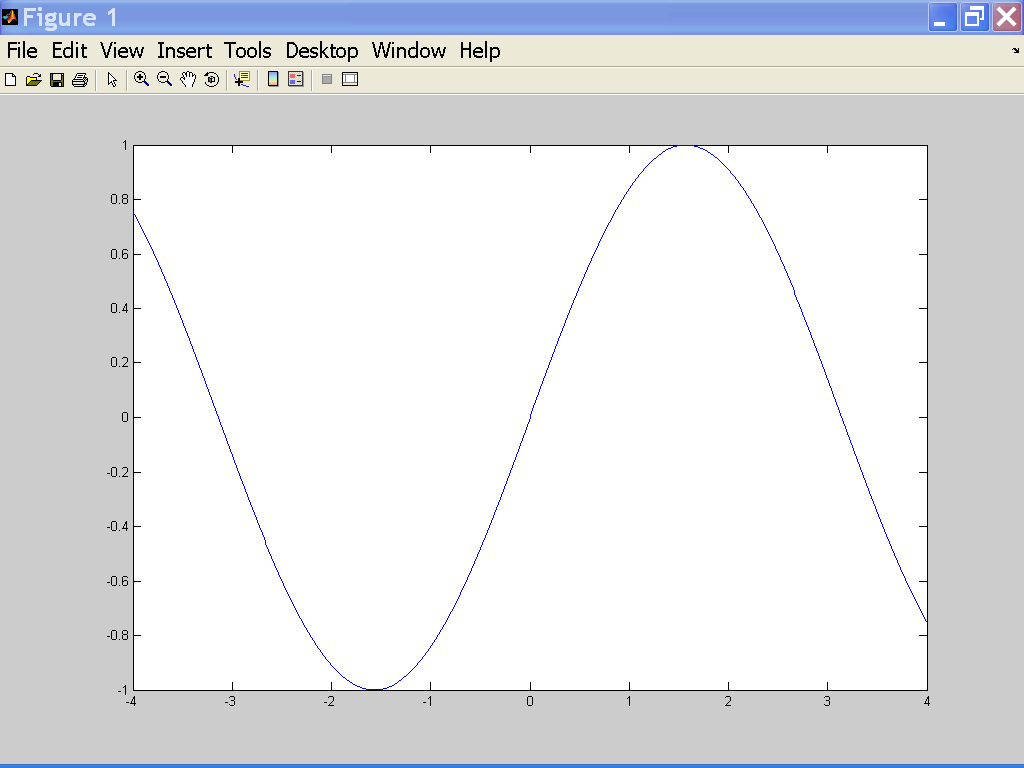
Рис. 3.2-1. Графическое окно с графиком функции y=sin(x)
В вышеописанном примере вектор xявляется набором равноотстоящих точек с шагом 0.01, а y- вектор со значениями функции синуса в этих точках. Для отображения графика системаMatLab открывает отдельное окно с именем Figure 1. Переход между окнами, то есть возврат в окно MatLab или переход от одного графического окна к другому графическому окну осуществляется в соответствии с правилами среды: с помощью команд основного меню; комбинации <Alt+Tab>или с помощью мыши.
Рассмотрим еще один пример построения графика y=e−x2на интервале
[-1.5 ;1.5].
| Пример 3.2-2 |
| >> x = - 1.5:.01:1.5; >> y = exp(-x.ˆ2); >> plot(x,y) >> |
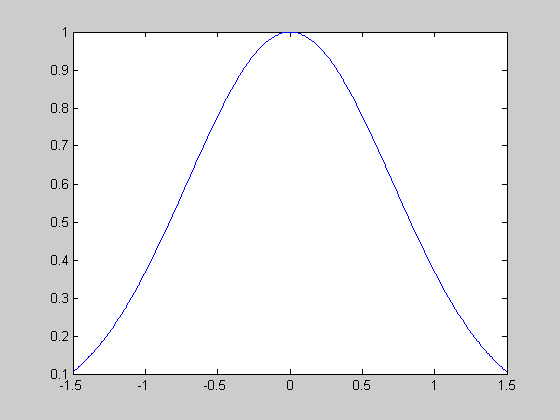
Рис. 3.2-2. График функции y=e−x2
Необходимо обратить внимание на то, что точка перед знаком возведения в степень (^)обязательна, поскольку мы хотим, чтобы возведение в степень выполнялось поэлементно.
В системеMatLab можно также построить кривые, заданные параметрически.
| Пример 3.2-3 |
| >> t=0:.001:2*pi; >> x=cos(3*t); >> y=sin(2*t); >> plot(x,y) >> |
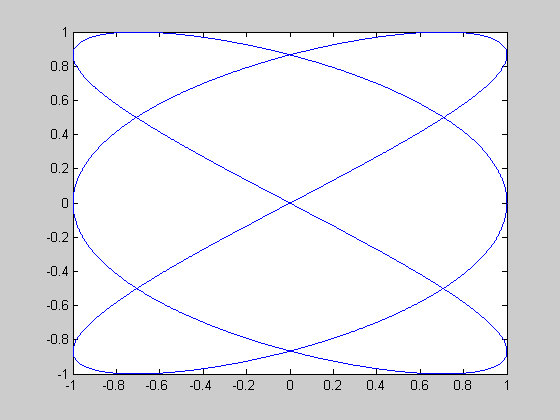
Рис. 3.2-3. График функции, заданный параметрически
Аргументами функции plot()могут быть различные комбинации векторов и матриц:
· plot(y):
· если y- вектор, то будет нарисована кривая yкак функция номера элемента в y;
· если y- матрица, то будет сгенерирован набор кривых, каждая из которых представляет собой зависимость столбца матрицы от номера строки.
· plot(x,y)
· если x и y - вектора одинаковой длины и размерности (оба строки или оба столбцы), то будет нарисована кривая yот x;
· если x - вектор, а y - матрица, строки или столбцы yбудут нарисованы в зависимости от x; если столбец матрицы y имеет ту же длину, что и вектор x, то будет построен набор кривых, представляющий зависимость каждого из столбцов от x; если строка матрицы y имеет ту же длину, что и вектор x, то будет построен набор кривых, представляющий зависимость каждой из строк от x; если число строк и столбцов y одинаково, то строятся столбцы от x;
· если x -матрица, а y -вектор, то будет построено несколько кривых, представляющих зависимость y от строк или столбцов матрицы x по правилу, описанному в предыдущем пункте;
· если x и y -матрицы одинаковой размерности, то будет построен набор кривых, представляющих столбцы y от столбцов x.
При вышеописанных способах вызова функции plot()различные кривые на одном и том же графике рисуются разным цветом. Перебор цветов выполняется автоматически, а при использовании соответствующих аргументов у команды plot()эти цвета можно выбирать.
В общем случае, число аргументов у команды plot()не ограничивается двумя, то есть plot(x1,y1,x2,y2,...), причем правила, описанные выше, относятся к каждой паре аргументов.
С помощью соответствующих команд любой график в графическом окне MatLab может быть снабжен заголовком, именами осей, и на сам график может быть помещен дополнительный текст с помощью команд вывода текста. На график можно так же поместить сетку. Аргументами всех этих команд является текстовая строка. Например, команда title('График наилучшего приближения')добавит к вашему графику заголовок. Команда gtext('Пятно')позволяет с помощью мыши или клавишного курсора разместить на рисунке индикаторный крест, в месте размещения которого и будет помещен текст после нажатия произвольной клавиши. При необходимости сделать подписи осей используются команды Xlabel('ПодписьX'), Ylabel('ПодписьY').
Для изображения нескольких кривых на одном рисунке существуют два способа, которые иллюстрируются следующими примерами.
| Пример 3.2-4а |
| >> x=0:.01:2*pi; >> y1=sin(x); >> y2=sin(2*x); >> y3=sin(4*x); >> plot(x,y1,x,y2,x,y3) >> |
| Пример 3.2-4b |
| >> x=0:.01:2*pi; >> Y=[sin(x)’, sin(2*x)’, sin(4*x)’]; >> plot(x,Y) >> |
Эти два примера полностью эквивалентны, а результат изображен на рис. 3.2-4. Отметим, что во втором примере формируется матрица Y, содержащая значения изображаемых функций в виде столбцов.
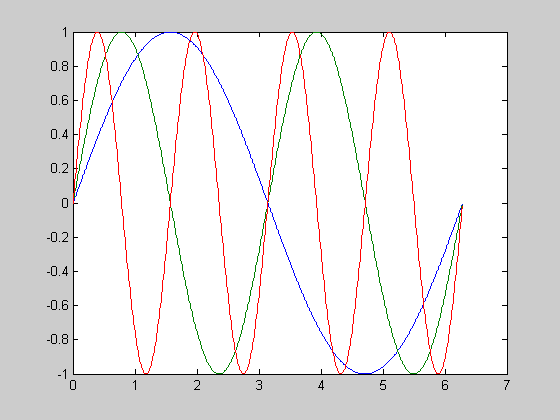
Рис 3.2-4. Графикифункцийy1=sin(x); y2=sin(2*x);y3=sin(4*x);
Другим способом такого отображения нескольких функции на одних осях является использование команды holdon, которая замораживает текущий график, так что последующие кривые размещаются на этом же графике. При этом масштаб и разметка осей изменяются, если новая кривая не вписывается в нарисованные оси. Команда holdoffприводит к тому, что любой последующий вызов команды plotсоздает новый рисунок в этом же окне, то есть предыдущий график стирается.
При выводе графика можно сменить принятый по умолчанию тип точек, с помощью которых рисуется данный график.
| Пример 3.2-5 |
| >> x=0:.01:2*pi; >> y1=sin(x); >> y2=sin(2*x); >> y3=sin(4*x); >> plot(x,y1,’--’,x,y2,’:’,x,y3,’+’) >> |
Результат работы программы приведет к тому, что первый график будет нарисован пунктиром, второй - точками, а третий - символами + (рис. 3.2-12). В общем случае каждая линия на графике определяется триплетом x,y,s, где xи y- это вектора с координатами функции, а s– строковая переменная, образованная любыми комбинациями из каких-нибудь приведенных ниже столбцов таблицы 3.2-5.
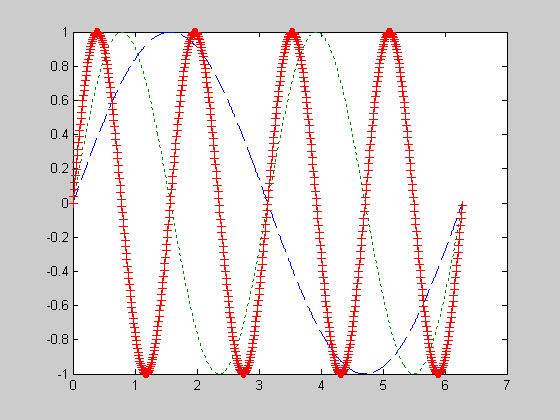
Рис. 3.2-5. Пример графика Sin(x), Sin(2x) и Sin(3x)
. Таблица 3.2-1
| S | Цвет | S | Маркер |
| y | желтый | . | точка |
| m | фиолетовыйo | кружок | : |
| c | голубой | x | x-метка |
| r | красный | + | плюс |
| g | зеленый | * | звездочка |
| b | синий | s | квадрат |
| w | белый | d | алмаз |
| k | черный | v | Треугольник(вниз) |
| € | треугольник (вверх) | - | сплошная |
| < | треугольник (влево) | точечная | |
| > | треугольник (вправо) | -. | Штрих - пунктирная |
| p | шестиугольник | - | пунктирная |
| h | восьмиугольник |
По умолчанию масштаб осей выбирается автоматически, таким образом, чтобы график целиком поместился в окне, причем с разумным запасом. Кроме того, оси автоматически размечаются, и по умолчанию выбирается, декартова система координат. Причем началом координат считается точка с координатами xmin, ymin, расположенная в левом нижнем углу. Эта автоматическая установка может быть изменена с помощью команды axis. Примеры использования этой команды применительно к плоским графикам описаны в табл. 2.5-9.
При необходимости вывести в одном графическом окне несколько графиков, то есть разбить графическое окно на несколько областей - подобластей, в каждой из которых отображаются свои оси, используется команда subplot(m,n,p). Значение mуказывает, на сколько областей окно разбивается по вертикали, n– по горизонтали, а p-порядковый номер подокна при счете слева направо и сверху вниз. Команда subplotиспользуется как для создания нового подокна, так и для перехода от одного подокна к другому. После вызова этой команды plotпостроит график или графики в соответствующем подокне. Например, последовательность команд Примера 3.2-6 строит два рисунка в верхней и нижней части экрана. В верхней части строится график sin(x), а в нижней части экрана - зависимость log(abs(sin(x))). Как видно из приведенной выше последовательности команд, при x=0вычисляется log(0). При этом в командном окне появляется предупреждение, а график строится в точках −1 ≤ x ≤ 0.1и 0.1 ≤ x ≤ 1.
Таблица 3.2-2
| Обращение | Результат |
| axis([xminxmaxyminymax]) | Устанавливает пределы изменения по xи yкоординатам соответственно. Если максимальный предел по любой координате установить равным Inf, то соответствующий предел будет определяться автоматически. Аналогичное справедливо для нижнего предела, если его установить равным -Inf. |
| axis(’square’) | Делает область вывода квадратной. |
| axis(’equal’) | Делает единицы измерения по оси xи yодинаковыми. |
| axis(’normal’) | Восстанавливает режим по умолчанию. |
| axis(’ij’) | Помещает начало координат в левый верхний угол. Направление оси x- слева направо, направление оси y- сверху вниз. |
| axis(’xy’) | Восстанавливает стандартную декартову систему координат с началом в левом нижнем углу и направлением оси yснизу вверх. |
| axis(’tight’) | Устанавливает пределы по осям точно равными максимальным и минимальным значениям соответствующих переменных. |
| axis(’off’) | Делает невидимыми оси, метки осей и надписи |
| axis(’on’) | Включает оси и их разметку. |
| Пример 3.2-6 |
| >> x= -1:.1:1; >> y1=sin(x); >> subplot(2, 1, 1), plot(x, y1); >> y2=log(abs(y1)); >> subplot(2, 1, 2), plot(x,y2); >> |
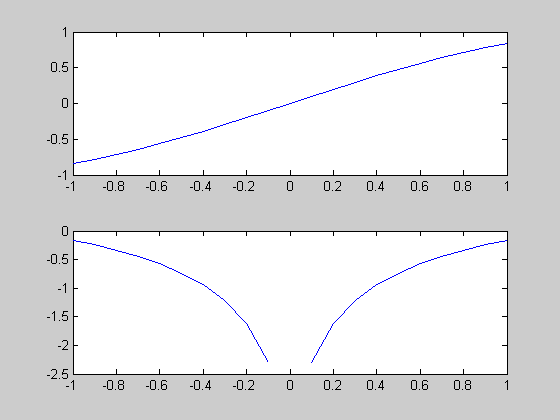
Рис.3.2-6. Две подобласти в одном графическом окне
Полярными координатами(ρ,θ)точки P (рис. 3.2-7) называются длина ρ радиус - вектора, проведенного из начала координат в точку P, и угол θ, образованный между осью х и этим вектором. Угол отсчитывается от положительного направления оси х к радиус-вектору против часовой стрелки.
Довольно многие математические кривые с целью устранения неоднозначности принято задавать в полярной системе координат.
Для построения графиков функций, заданных в полярной системе координат, вместо функции plotиспользуется функция polar:
| Пример 3.2-7 | ||
| >> phi=0:0.1:2*pi; >>ro=5*(i+cos(phi)); >> polar(phi,ro); >> title {'Кардиоида'); >> | ||
Результат построения кардиоиды дляа=5 приведен на рис. 3.2-7.
Рис.3.2-7.График кардиоиды в полярной системе координат
Единицы измерения значений ординат и абсцисс далеко не всегда соответствуют друг другу, и для создания более обозримого графика вдоль одной или обеих координатных осей приходится выбирать логарифмический масштаб. Для построения таких графиков используются функции loglog(логарифмический масштаб по обеим осям), semilogx (логарифмический масштаб по оси x), semilogy (логарифмический масштаб по оси у).
| Пример 3.2-7 |
| >> x=0:10:100; >> y=exp(x); >>semilogy(x,y) >> |
Результат построения графика в логарифмическом масштабе приведен на
рис.3.2-8.
Рис. 3.2-8.График с логарифмическим масштабом по оси у
Довольно интересной модификацией функции plot является функция fplot, которая строит график функции y=f(x)без предварительного вычисления векторов (x1,x2,…) и (y1,y2,...). Базовый формат вызова этой функции включает два аргумента:
fplot (@name_fun, [limits])
fplot (' name_fun', [limits])
В первом случае первым аргументом является указатель на функцию с именем name_fun, во втором случае - строка с именем обрабатываемой функции. Аргумент limitsможет быть представлен либо двухкомпонентным вектором [xminхmах], либо четырехкомпонентным вектором [xminxmaxyminymax]. Укороченный вариант задает пределы изменения аргумента х, расширенный - дополнительно представляет пределы изменения функции. Например:
fplot(@sin, [0 2*pi])
fplot('sin', [0 2*pi])
По сравнению с plot функция fplotберет на себя вычисление таблицы значения функции, проявляя при этом некоторый интеллект - в местах резкого изменения функции значения аргумента х выбираются с более мелким шагом. Функция fplot гарантирует, что относительное уклонение воспроизводимой функции отличается от ее идеального графика не более чем на 0,2%. Если вам нужен более точный или более грубый график, то после двух обязательных аргументов в функции fplot можно задать желаемую относительную погрешность - число, меньшее 1:
fplot(@sin, [0 2*pi], 0.05)
В этом случае гарантировано построение графика, отличающегося от идеальной кривой не более чем на 5%. По умолчанию точность равна 2・10−3, и она определяет, на сколько точек делить интервал, чтобы погрешность от линейной интерполяции не превосходила этой заданной точности.
Еще один дополнительный параметр — целое натуральное число n требует, чтобы функция fplot использовала при построении не менее чем n+1точку. Относительная погрешность и количество точек могут задаваться в любом порядке:
fplot(@sin, [0 2*pi], 0.05, 20)
fpiot(@sin, [0 2*pi], 20, 0.05)
Наконец, как и в функции plot, среди дополнительных параметров могут находиться строки, управляющие цветом и маркировкой графика. Последовательность задания всех дополнительных параметров – произвольная. Результат выполнения следующего оператора приведен на рис. 3.2-16.
| Пример3.2-9 |
| >>fplot(@sin, [0 2*pi], 0.05, 's--') >> |
Рис. 3.2-9. Синусоида, построенная c помощью функции fplot
Функция fplot умеет возвращать значения компонентов векторов х и у, если к ней обратиться следующим образом:
[х у] = fplot(@sin, [0 2*pi]);
В этом случае кривая не рисуется, а соответствующие координаты заносятся в массивы x и y соответственно.
Функция f, указываемая в качестве первого аргумента fplot, кроме независимой переменной хможет содержать дополнительные параметры, например, y=f(x,a1,a2). Тогда эти параметры указываются среди дополнительных аргументов после задания относительной погрешности и минимального числа точек:
fplot('nanie_fun’, [xl х2], 0.05, 20, al, a2)
Рассмотрим Пример 3.2-10, результат которого отображен на рис. 3.2 -10.
| Пример3.2-10 |
| >> subplot (1, 2,1); >>fplot('[tan(x),sin(x),cos(x)]',2*pi*[-l 1 -1 1]); >> subplot (2, 2,2); >>fplot('sin(l / x)', [0.01 0.1); >> |
Рис. 3.2-10. Примеры работы функции fplot
Функция fplot() предоставляет альтернативную возможность изображения функций по сравнению с вычислением вектора y по x и последующим изображением этой кривой с помощью функции plot(). Эта функция бывает особенно полезной, когда кривая имеет несколько разных скоростей изменения и заранее не ясно, в скольких и каких точках необходимо вычислять и выводить кривую. Этой функции необходимо передавать строку, описывающую требуемую функцию в виде f(x). Строка, описывающая f(x), может содержать любые допустимые в MatLab операции и/или функции. Функция f(x) должна возвращать вектор той же размерности, что и x, или матрицу, каждый столбец которой имеет столько же элементов, сколько и x.
Например, для того чтобы нарисовать кривую y = sin(x)•cos(2x) в диапазоне x от 0 до 5π, необходимо вызвать функцию fplot (’sin(x) .*cos(2x)’, [0 5*pi]).
График с двумя осями ординат (одна ось отображается слева, другая ось справа) реализуется функцией plotyy(x1,y1,x2,y2) и той же функцией с добавлением параметров масштабирования 'f1' или 'f1','f2', в роли которых могут выступатьplot, semilogx,semilogx, loglog (рис. 3.2-11).
| Пример3.2-11 |
| >> x=0:0.01:12*pi; >>plotyy(x,sin(x).*exp(-0.1.*x),x, 10*exp(-0.1.*x)) % |
Рис. 3.2-11. Графическое окно с двумя осями координат
Для размещения различных надписей на полученном рисунке применяют функции xlabel, ylabel, titleиtext. Функция xlabelпредназначена для размещения горизонтальной оси, функция ylabel– названия вертикальной оси. Для размещения надписи в произвольном месте рисунка используется функция text, а общий заголовок для графика выводится функцией title. Кроме того, используя команду gridonможно нанести измерительную сетку.
Рассмотрим пример 3.2-12, результат которого приведен на рис. 3.2-12.
| Пример3.2-12 |
| >> x=1.5 : 0.1 : 2.5; >> y=sin(x); >> title (‘График sin(x)’); >>xlabel(‘осьх’); >>ylabel(‘sin(x)’); >> text(2.1,0.9,f(x)=sin(x)’); >>grid on >>plot(x, y) >> |
Рис. 3.2-12
В системе MatLabсуществует функция, которая создает ступенчатое изображение ваших данных. Например, вместо соединения каждой пары точек из векторов аргументов прямыми линиями (как это делает функция plot() или line()) функция stairs() изображает ваши данные в виде горизонтальных отрезков на уровне yi, причем каждый отрезок горизонтальной линии длится от iдо i + 1, если обращение имеет вид stairs(y), и от xi до xi+1, если обращение имеет вид stairs(x,y). Значения xi не должны быть равноотстоящими и не должны быть упорядочены по возрастанию. Вывод графика на экран можно предотвратить, используя обращение вида [xs,ys]=stairs(x,y). Потом этот график может быть выведен на экран с помощью команды plot(),line()или другим каким-нибудь способом.
