Энергоемкость страховочного уса

Если мы беспокоимся о своем здоровье и запасе энергоемкости нашей страховочной системы, то наши страховочные усы будут иметь максимально возможную энергоемкость. Для этого они должны быть сделаны из добротной динамической веревки. Оптимальный диаметр веревки для усов: 9 - 10 мм.

Даже та небольшая длина динамической веревки, что составляет ус, обладает значительной в условиях микро-падения энергоемкостью, способной серьезно смягчить динамическую пиковую нагрузку при его остановке.

Опираясь на паспортные данные современных динамических веревок, можно четко сказать, что те полметра ее, заключенные в длинном усе между узлами дадут при остановке падения до 10-15 см удлинения при пиковых нагрузках не более 600 кГ. А это значит, что энергоемкость только прямой (между узлами) части длинного уса составит порядка 75-90 кГм при нагрузках до 600 кГ.

Куда больше чем мы сами в беседке!

Как мы установили ранее, общая глубина нашего возможного падения с повисанием на длинном страховочном усе колеблется от 0,35 м из положения спуска до 0,68 м из положения подъема. Без учета рапели длина страховочной цепи, участвующей в остановке падения - 0,8 м. При весе падающего 80 кГ энергия такого падения, подлежащая рассеиванию, составит около 65 кГм. При весе 100 кГ соответственно около 80 кГм.

Простое сравнение величины потенциальной энергии и энергоемкости прямой части уса показывает, что ус прекрасно справится с задачей даже без учета нашего тела в беседке и участочка веревки выше страховочного зажима.

Следовательно, их суммарное участие в остановке падения еще более понизит пиковую ударную нагрузку при остановке микро-падения.

Но и это еще не все, так как кроме прямого участка веревки уса в амортизации рывка принимают участие его узлы.

Эффект границы Lo (Но)

В русскоязычную терминологию это понятие пришло также из книги Петко Недкова "А Б В на техниката на единичното въже", где Петко пишет.

"Как видно из диаграммы (см. Рис.22), сила нагрузки на веревку (пиковой нагрузки при остановке падения, прим. мои, КБС) до тех пор не может достичь максимума для данного фактора падения, пока глубина падения H, а соответственно и длина останавливающей его веревки, будут меньше некоторой определенной минимальной величины. Это, так называемая, граница Hо (Аш нулевое), после которой величина пиковой динамической нагрузки входит в соответствие с величиной фактора падения".

Рис.22. Кривая зависимости величины пиковой динамической нагрузки (Р)при остановке падения от длины веревки, его останавливающей (L), представляет собой прямую линию, параллельную оси абсцисс, так как не зависит от глубины падения. И только в самом начале изменяется от0до некоторой величиныLо, после которой закон вступает в силу, и пиковая нагрузка перестает зависеть от глубины падения и длины веревки (поПетко Недкову).

На мой взгляд, термин "Граница Аш-нулевое" не очень удачен, так как обозначает вроде бы глубину падения - Н, а описывает по сути свойства веревки. Резоннее было бы говорить о величине Lo ("Эль нулевое"), некоей длине веревки, после которой величина пиковой динамической нагрузки при остановке падения перестает зависеть от длины веревки, его останавливающей.

Суть явления заключается в том, что если взять ряд образцов одной и той же веревки все увеличивающейся длины, завязать на концах узлы, одним из которых крепить к опоре, а к другому - сбрасываемый с одинаковым фактором груз одинаковой массы, то у самых коротких образцов - короче некоей величины Lо, (которая у Петко Недкова называется Но), величина пиковой динамической нагрузки при остановке падения будет меньше, чем у всех остальных, у которых эта величина, в конце концов, станет постоянной и не зависящей от их длины.

Петко пишет:

"Если осуществить ряд последовательных падений данного груза с фактором 1,0, в каждом последующем случае привязанного к веревке большей, чем в предыдущем, длины, и измерить величины возникающих при этом динамических нагрузок, то мы получим кривую, которая вначале стремительно идет вверх, все более выполаживаясь, пока не достигнет некоей границы Hо, после чего превращается в прямую, параллельную оси абсцисс".

То есть все образцы, превышающие длиной эту величину - я называю ее сейчас Lо, останавливают падение с одинаковой нагрузкой, вне зависимости от их длины и - следовательно, глубины падения. Как собственно и положено согласно закону падения груза на веревке, когда величина рывка не зависит от глубины падения и пропорциональна корням квадратным из величины веса падающего, фактора падения и коэффициента эластичности (жесткости) веревки.

Эффект границы Lо (Ho) весьма полезен для техники одинарной веревки, так как уменьшает величину пиковой динамической нагрузки на веревку при ее длине, меньшей некоего значения Lо, своего для каждой конкретной веревки.

Эффект Lо объясняется тем, что в амортизации энергии принимает участие веревка, заключенная в узлах, а также сами узлы - как конструкции из веревки, гасящие энергию падения за счет внутреннего трения между витками.

Это значит, что пока энергоемкость узлов на концах веревки сравнима с энергией падения - она заметна. Конечно, заметна лишь на очень малых глубинах падения, а далее работа узлов просто теряется в тех масштабах энергий, которые возникают при падении и поглощаются веревкой при его остановке.

На практике мы используем это полезное свойство узлов в двух случаях. При изготовлении страховочных усов с узлами на концах и при навеске - задавая расстояние между основным и дублирующим закреплением, не превышающее границу Lo(Рис.23).

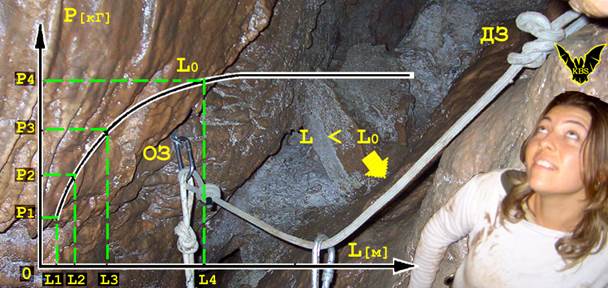
Рис.23. Зависимость пиковой динамической нагрузки (ПДН - Р) при разрушении основного закрепления (ОЗ) в зависимости от длины веревки (L) между ним и дублирующим (ДЗ) закреплениями при одинаковом факторе падения (по Петко Недкову).

Длина веревки междуОЗиДЗ, а также длина страховочного уса всегда должны быть меньше границыLoдля той веревки, из которой делаем навеску или страховочные усы.

Петко Недков пишет:

"Эффект границы Hо имеет практическое значение только для коротких кусков веревки, например, в случае с самостраховочным "усом", или для участка веревки, связывающей основное и дублирующее закрепления. Иными словами, если при дублировании закреплений связывающая их часть веревки окажется длиннее величины Hо, то данное дублирующее закрепление не сможет быть полезным для уменьшения пиковой динамической нагрузки в случае, если основное закрепление разрушится.

Величина границы Hо зависит, в основном, от фактора падения и от вида веревки, но на нее также влияет и ее состояние - мокрая, сухая, более или менее изношенная и т.п.".

Энергоемкость узлов из данной веревки, конечно, зависит от состояния веревки, но для данного ее состояния является величиной постоянной. Меняется только фактор падения, и этим меняется доля энергоемкости узлов в энергии падения. Чем больше фактор падения, тем больше энергия падения, которую надо поглотить, и тем пропорционально меньшую лепту в этот процесс могут внести узлы.

Как же определить и учитывать величину границы Lo (Но) в практической работе? Петко пишет:

"В целях практической работы по навешиванию отвесов можно принять, что для динамических веревок величина Hо будет порядка 1,5 м, а для статических - не более 1 м длины веревки между закреплениями при факторе падения 1,0.

ЗАПОМНИ:

- Соблюдение границы Hо (сообразно применяемой в данный момент веревке) имеет значение для обеспечения надежности дублирующего закрепления".

Итак, при малых глубинах, а, следовательно, и энергиях падения зависимость пиковой динамической нагрузки Рmax от массы падающего G,фактора падения f и относительного удлинения веревки (j=Dl/l) - утрачивает свою линейность.

Но только в самом начале - при малых глубинах и энергиях падения!

Прекрасно видно, что длина нашего страховочного уса и глубина микро-падений на нем таковы, что лежат внутри этой границы Lo. Это дает нам дополнительное смягчение ударной нагрузки, если ус изготовлен из динамической веревки с узлами. Усы из малоэластичной веревки с узлами тоже обладают определенной энергоемкостью, но значительно ниже, чем из динамической, что делает их опасными в ситуациях микро-падений с высокими факторами.

Все остальные варианты страховочных усов подобным смягчающим эффектом не обладают. Кроме, конечно, самостраховочных систем на основе амортизаторов - как фрикционных, так и разрывных.